задание. Контрольные работы новые. Правила выполнения и оформления контрольных работ
 Скачать 152.75 Kb. Скачать 152.75 Kb.
|
|
Контрольные работы по математике Правила выполнения и оформления контрольных работ В соответствии с учебным планом в процессе изучения курса математики студент должен выполнить 3 контрольных работы. Первая и вторая контрольные работы выполняются студентами 1 курса. Третья контрольная работа выполняются студентами 2 курса. При выполнении контрольных работ студент должен руководствоваться следующими указаниями: Работы должны выполняться в тетради (в клетку), на внешней обложке которой должен быть прикреплен титульный лист. Контрольные задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением каждой задачи надо полностью переписать ее условия. Решение задач следует излагать подробно, делая соответствующие ссылки на вопросы теории с указанием необходимых формул, теорем. Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должны соответствовать обозначениям, приведенным на чертежах. На каждой странице тетради необходимо оставлять поля шириной 3-4см для замечаний преподавателя. Контрольные работы должны выполняться самостоятельно. Не самостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена. Задания, выполненные не полностью или не по своему варианту, не засчитываются и возвращаются студенту. Выполненные работы студенты отправляют почтой на проверку в ДВИК. После получения прорецензированной работы студенту необходимо исправить отмеченные ошибки, выполнить все указания и повторить недостаточно усвоенный материал. Если контрольные задания не зачтены, то студент их выполняет вторично (тот же вариант или новый по указанию преподавателя). На экзамене студенту необходимо контрольные работы иметь при себе. Сдача экзамена разрешается студенту, получившему положительную оценку по всем контрольным работам. Каждый студент выполняет контрольные работы своего варианта. Номер варианта определяется по последней цифре номера зачетки. Зная номер своего варианта от 0 до 9, студенты по таблице определяют номера вопросов контрольных работ. Ниже приведены таблицы номеров задач для контрольных работ. Таблица вариантов к контрольной работе №1
Таблица вариантов к контрольной работе №2
Таблица вариантов к контрольной работе №3
Задания к контрольной работе №3. Интегральное исчисление функции одной переменной. 1-10. Найти неопределённые интегралы: 1. а) 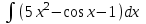 ; б) ; б) 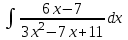 ; в) ; в) 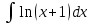 . .2. а) 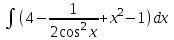 ; б) ; б)  ; в) ; в) 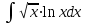 . .3. а) 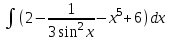 ; б) ; б) 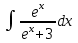 ; в) ; в) 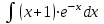 . .4. а) 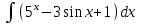 ; б) ; б) 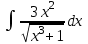 ; в) ; в) 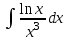 . .5. а) 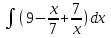 ; б) ; б) 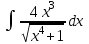 ; в) ; в) 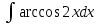 . .6. а) 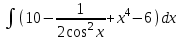 ; б) ; б) 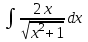 ; в) ; в) 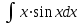 . .7. а) 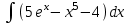 ; б) ; б) 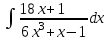 ; в) ; в) 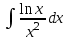 . .8. а) 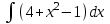 ; б) ; б) 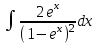 ; в) ; в) 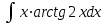 9. а) 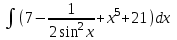 ; б) ; б) 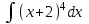 ; в) ; в) 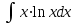 . .10. а) 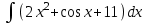 ; б) ; б) 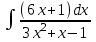 ; в) ; в) 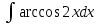 . .11-20. Вычислить определенные интегралы с точностью до 10-2. а) 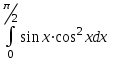 ; б) ; б)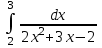 . .а) 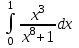 ; б) ; б)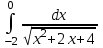 . .а) 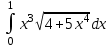 ; б) ; б)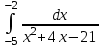 . .а) 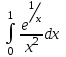 ; б) ; б)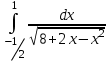 . .а) 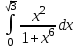 ; б) ; б)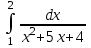 . .а) 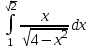 ; б) ; б)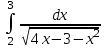 . .а) 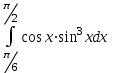 ; б) ; б)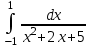 . .а)  ; б) ; б)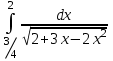 . .а)  ; б) ; б)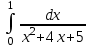 . .а) 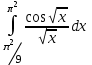 ; б) ; б) . . 21-30. Вычислить несобственные интегралы или доказать их расходимость. 21. 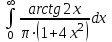 ; 22. ; 22. 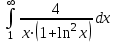 ; 23. ; 23. 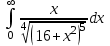 ; ; 24. 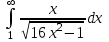 ; 25. ; 25. 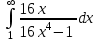 ; 26. ; 26. 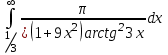 ; ;27. 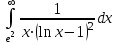 ; 28. ; 28. 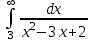 ; 29. ; 29. 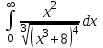 ; 30. ; 30. 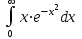 . .Дифференциальные уравнений. 31-40. Найти общее решение дифференциального уравнения. а) 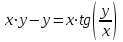 ; б) ; б) 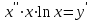 ; ;а) 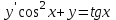 ; б) ; б) 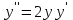 ; ;а) 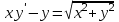 ; б) ; б) 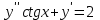 ; ;а)  ; б) ; б) 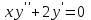 ; ;а) 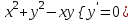 ; б) ; б) 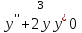 ; ;а) 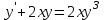 ; б) ; б) 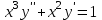 ; ;а) 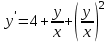 ; б) ; б) 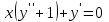 ; ;а) 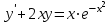 ; б) ; б) 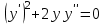 ; ;а) 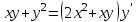 ; б) ; б) 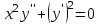 ; ;а) 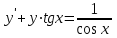 ; б) ; б) 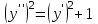 . .41-50. Найти частное решение дифференциального уравнения, удовлетворяющего начальным условиям. 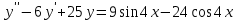 , , 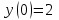 , , 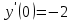 . .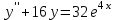 , , 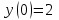 , , 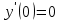 . .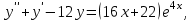 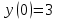 , , 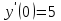 . .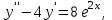 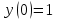 , ,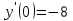 . .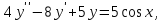  , ,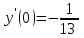 . .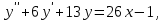  , , 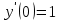 . .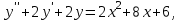 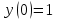 , , 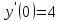 . .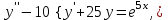 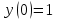 , , 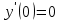 . .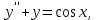 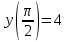 , ,  . .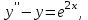 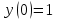 , ,  . .Теория вероятностей. 61. Решить задачи: 1. Из пяти букв разрезной азбуки составлено слово “песня”. Ребёнок, не умеющий читать, рассыпал буквы и затем собрал их в произвольном порядке. Найти вероятность того, что у него снова получилось слово “песня”. 2. В телестудии три телевизионные камеры. Вероятности того, что в данный момент камера включена, соответственно равны: 0,9; 0,8; 0,7. Найти вероятность того, что в данный момент включены: а) две камеры; б) не более одной камеры; в) три камеры. 3. 20 % приборов монтируется с применением микромодулей, остальные – с применением интегральных схем. Надёжность прибора с применением микромодулей – 0,9, интегральных схем – 0,8. Найти: а) вероятность надёжной работы наугад взятого прибора; б) вероятность того, что прибор – с микромодулем, если он был исправен. 4. Всхожесть семян некоторого растения составляет 80 %. Найти вероятность того, что из 6 посеянных взойдут: а) три; б) не менее трёх; в) четыре. 62. Решить задачи: Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлечённый кубик будет иметь две окрашенные грани. На железобетонном заводе изготовляют панели, 90 % из которых – высшего сорта. Какова вероятность того, что из трёх наугад выбранных панелей высшего сорта будут: а) три панели; б) хотя бы одна панель; в) не более одной панели? Детали попадают на обработку на один из трёх станков с вероятностями, соответственно равными: 0,2; 0,3; 0,5. Вероятность брака на первом станке равна 0,02, на втором – 0,03, на третьем – 0,01. Найти: а) вероятность того, что случайно взятая после обработки деталь – стандартная; б) вероятность обработки наугад взятой детали на втором станке, если она оказалась стандартной. В семье четверо детей, принимая равновероятным рождение мальчика и девочки, найти вероятность того, что мальчиков в семье: а) три; б) не менее трех; в) два. 63. Решить задачи: В группе спортсменов 7 лыжников и 3 конькобежца. Из нее случайным образом выделены три спортсмена. Найти вероятность того, что все выбранные спортсмены окажутся лыжниками. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,7. Оба стрелка сделали по одному выстрелу. Какова вероятность того, что цель поражена: а) хотя бы один раз, б) два раза; в) один раз? Комплектовщик получает для сборки 30 % деталей с завода № 1, 20 % – с завода № 2, остальные – с завода № 3. Вероятность того, что деталь с завода № 1 – высшего качества, равна 0,9, для деталей с завода № 2 – 0,8, для деталей с завода № 3 – 0,6. Найти вероятность того, что: а) случайно взятая деталь – высшего качества; б) наугад взятая деталь высшего качества изготовлена на заводе № 2. Вероятность успешной сдачи студентом каждого из пяти экзаменов равна 0,7. Найти вероятность успешной сдачи: а) трех экзаменов; б) двух экзаменов; в) не менее двух экзаменов. 64. Решить задачи: Из партии втулок, изготовленных за смену токарем, случайным образом отбирается для контроля 10 шт. Найти вероятность того, что среди отобранных втулок две – второго сорта, если во всей партии 25 втулок первого сорта и 5 – второго. В блок входят три радиолампы. Вероятности выхода из строя в течение гарантийного срока для них соответственно равны: 0,3; 0,2; 0,4. Какова вероятность того, что в течение гарантийного срока выйдут из строя: а) не менее двух радиоламп; б) ни одной радиолампы; в) хотя бы одна радиолампа? Среди поступивших на сборку деталей 30 % – с завода № 1, остальные – с завода № 2. Вероятность брака для завода № 1 равна 0,02, для завода № 2 – 0,03. Найти: а) вероятность того, что наугад взятая деталь стандартная; б) вероятность изготовления наугад взятой детали на заводе № 1, если она оказалась стандартной. Среди заготовок, изготавливаемых рабочим, в среднем 4 % не удовлетворяют требованиям стандарта. Найти вероятность того, что среди 6 заготовок, взятых для контроля, требованиям стандарта не удовлетворяют: а) не менее пяти; б) не более пяти; в) две. 65. Решить задачи: В лифт шестиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выйдет на любом из этажей, начиная со второго. Найти вероятность того, что все пассажиры выйдут на четвертом этаже. В первом ящике 20 деталей, 15 из них – стандартные, во втором ящике 30 деталей, 25 из них – стандартные. Из каждого ящика наугад берут по одной детали. Какова вероятность того, что: а) обе детали будут стандартными; б) хотя бы одна деталь стандартная; в) обе детали нестандартные? Три автомата изготовляют однотипные детали, которые поступают на общий конвейер. Производительности первого, второго и третьего автоматов соотносятся как 2:3:5. Вероятность того, что деталь с первого автомата – высшего качества, равна 0,8, для второго – 0,6, для третьего – 0,7. Найти вероятность того, что: а) наугад взятая с конвейера деталь окажется высшего качества; б) взятая наугад деталь высшего качества изготовлена первым автоматом. Вероятность выигрыша по одной облигации трехпроцентного займа равна 0,25. Найти вероятность того, что из восьми купленных облигаций выигрышными окажутся: а) три; б) две; в) не менее двух. 66. Решить задачи: Из букв разрезной азбуки составлено слово “ремонт”. Карточки с отдельными буквами тщательно перемешивают, затем наугад вытаскивают 4 карточки и раскладывают их в порядке извлечения. Какова вероятность получения при этом слова “море”? При одном цикле обзора трех радиолокационных станций, следящих за космическим кораблем, вероятности его обнаружения соответственно равны: 0,7; 0,8; 0,9. Найти вероятность того, что при одном цикле обзора корабль будет обнаружен: а) тремя станциями; б) не менее чем двумя станциями; в) ни одной станцией. Заготовка может поступить для обработки на один из двух станков с вероятностями 0,4 и 0,6 соответственно. При обработке на первом станке вероятность брака составляет 2 %, на втором – 3 %. Найти вероятность того, что: а) наугад взятое после обработки изделие – стандартное; б) наугад взятое после обработки стандартное изделие обработано на первом станке. Вероятность работы каждого из семи моторов в данный момент равна 0,8. Найти вероятность того, что в данный момент включены: а) хотя бы один мотор; б) два мотора; в) три мотора. 67. Решить задачи: Из восьми книг две художественные. Найти вероятность того, что среди взятых наугад четырех книг, хотя бы одна художественная. Вычислительная машина состоит из четырех блоков. Вероятность безотказной работы в течение времени Tпервого блока равна 0,4, второго – 0,5, третьего – 0,6, четвертого – 0,4. Найти вероятность того, что в течение времени Т проработают: а) все четыре блока; б) три блока; в) не менее трех блоков. На двух станках обрабатываются однотипные детали. Вероятность брака для станка № 1 составляет 0,03, для станка № 2 – 0,02. Обработанные детали складываются в одном месте, причем деталей, обработанных на станке № 1, вдвое больше, чем на станке № 2. Найти вероятность того, что: а) взятая наугад деталь будет стандартной; б) наугад взятая стандартная деталь изготовлена на первом станке. В телеателье имеется 7 телевизоров. Для каждого телевизора вероятность того, что в данный момент он включен, равна 0,6. Найти вероятность того, что в данный момент включены: а) четыре телевизора; б) хотя бы один телевизор; в) не менее трех телевизоров. 68. Решить задачи: На полке 6 радиоламп, из которых две негодные. Случайным образом отбираются две радиолампы. Какова вероятность того, что они годны для использования? Трое рабочих собирают подшипники. Вероятность того, что подшипник, собранный первым рабочим – высшего качества, равна 0,7, вторым – 0,8, третьим – 0,6. Для контроля взято по одному подшипнику из собранных каждым рабочим. Какова вероятность того, что высшего качества будут: а) все подшипники; б) два подшипника; в) хотя бы один подшипник? В дисплейном классе имеется 10 персональных компьютеров первого типа и 15 второго типа. Вероятность того, что за время работы на компьютере первого типа не произойдет сбоя, равна 0,9, а на компьютере второго типа – 0,7. Найти вероятность того, что: а) на случайно выбранном компьютере за время работы не произойдет сбоя; б) компьютер, во время работы на котором не произошло сбоя, – первого типа. При массовом производстве полупроводниковых диодов вероятность брака при формовке равна 0,1. Найти вероятность того, что из восьми диодов, проверяемых ОТК, бракованных будет: а) два; б) не менее двух; в) не более двух. 69. Решить задачи: В запасе ремонтной мастерской 10 поршневых колец, три из них восстановленные. Определить вероятность того, что среди взятых наугад четырех колец два окажутся восстановленными? На сборку поступают детали с трех станков с ЧПУ. Первый станок дает 20 %, второй – 30 %, третий – 50% однотипных деталей, поступающих на сборку. Найти вероятность того, что из трех наугад взятых деталей: а) три с разных станков; б) три с третьего станка; в) две с третьего станка. В пяти ящиках с 30 шарами в каждом содержится по 5 красных шаров, в шести других ящиках с 20 шарами в каждом – по 4 красных шара. Найти вероятность того, что: а) из наугад взятого ящика наудачу взятый шар будет красным; б) наугад взятый красный шар содержится в одном из первых пяти ящиков. Вероятность поражения мишени для данного стрелка в среднем составляет 80 %. Стрелок произвел 6 выстрелов по мишени. Найти вероятность того, что мишень была поражена: а) пять раз; б) не менее пяти раз; в) не более пяти раз. 70. Решить задачи: Десять студентов условились ехать определенным рейсом электропоезда с 10 вагонами, но не договорились о номере вагона. Какова вероятность того, что ни один из них не встретится с другим, если возможности в размещении студентов по вагонам равновероятны? Первый станок-автомат даёт 1 % брака, второй – 1,5 %, а третий – 2%. Случайным образом отобрали по одной детали с каждого станка. Какова вероятность того, что стандартными окажутся: а) три детали; б) две детали; в) хотя бы одна деталь? По линии связи передано два сигнала типа А и В с вероятностями соответственно 0,8 и 0,2. В среднем принимается 60 % сигналов типа А и 70 % типа В. Найти вероятность того, что: а) посланный сигнал будет принят; б) принятый сигнал типа А. Вероятность сдачи экзамена для каждого из шести студентов равна 0,8. Найти вероятность того, что экзамен сдадут: а) пять студентов; б) не менее пяти студентов; в) не более пяти студентов. |
