Предмет статики. Основные понятия и определения
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
|
43. Выражение скорости и ускорения точки вращающегося тела в виде векторных произведений. П 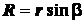 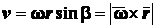 роведем из произвольной точки роведем из произвольной точки 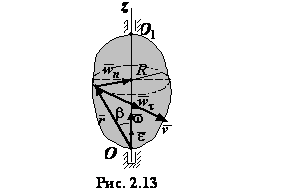 адиус-вектор адиус-вектор г 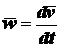 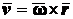 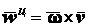 де символом де символом 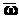 и радиуса-вектора и радиуса-вектора 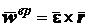 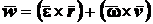 Легко показать, что вектор  направлен по касательной к траектории точки в одну сторону со скоростью, если вращение ускоренное, и в противоположную сторону, если оно замедленное, а вектор направлен по касательной к траектории точки в одну сторону со скоростью, если вращение ускоренное, и в противоположную сторону, если оно замедленное, а вектор 4. План решения задач статики. Решаемые методом статики задач могут быть одного из следующих типов: 1. Задачи, в которых известны действующие на тело силы и требуется найти, в каком положении или при каких соотношениях между действующими силами тело будет находиться в равновесии. 2. Задачи, в которых известны, что тело заведомо находится в равновесии и требуется найти чему равны при этом все или некоторые из действующих на тело сил. Реакции связей является величинами на перёд известными во всех задачах статики. Приступая к решению любой задачи, следует прежде всего установить равновесие какого тела (тел) надо рассмотреть, чтобы найти искомую величину. Процесс решения сводится к следующим операциям: 1. Выбор тела (тел), равновесие которого должно быть рассмотрено. 2. Изображение действующих сил. 3. Составление условий равновесия. 4. Определение искомых величин. 5. Проверка правильности решения и исследование полученных результатов. 7. Теорема о трех силах Если приложенные к твердому телу три непараллельные силы, лежащие в одной плоскости, находятся в равновесии, то линии действия этих сил пересекаются в одной точке. Положим, что тело находится в равновесии под действием трех сил Согласно первой аксиоме статики для равновесия тела необходимо и достаточно, чтобы сила Следует заметить, что выведенное условие равновесия трех непараллельных сил является необходимым, но не достаточным, т. е. мы можем утверждать, что если три непараллельные силы находятся в равновесии, то их линии действия пересекаются в одной точке, но мы не вправе сделать обратного заключения. Если линии действия трех сил пересекаются в одной точке, то отсюда вовсе не следует, что эти три силы представляют собой уравновешенную систему сил. 8. Расчет усилий в стержнях фермы методом вырезания узлов Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов, определению усилий в стержнях фермы. Активные силы и реакции опор являются внешними силами для всей фермы, рассматриваемой как твердое тело; усилия в стержнях в этом случае - внутренние силы. Поэтому для определения усилий необходимо рассмотреть равновесие части фермы, для которой искомые усилия являются внешними силами. При решении задач на расчете ферм способом вырезания узлов необходимо придерживаться следующего плана действий: 1. Выбор тела (или тел), равновесие которого должно быть рассмотрено. Для решения задачи надо рассмотреть равновесие тела, к которому приложены заданные и искомые силы или силы, равные искомым (например, если надо найти давление на опору, то можно рассмотреть равновесие тела, к которому приложена численно равная этой силе реакция опоры и т. п.). 2. Когда заданные силы действуют на одно тело, а искомые на другое или когда те и другие силы действуют одновременно на несколько тел, может оказаться необходимым рассмотреть равновесие системы этих тел или последовательно равновесие каждого тела в отдельности. 3. Изображение действующих (активных) сил. Установив равновесие какого тела или тел рассматривается (и только после этого), следует на чертеже изобразить все действующие на это тело, (или тела) внешние силы, включая как заданные, таи и искомые сковы, в том числе реакции всех связей. 4. Составление условий равновесия. Условия равновесия составляют для сил, действующих на тело (или тела), равновесие которых рассматривается. 5. Определение, реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматриваемой как твердое тело, проверка правильности решения и исследование полученных результатов. 6. Вырезать узел, в котором сходятся два стержня, и рассмотреть его равновесие под действием активных сил и реакций разрезанных стержней; определить эти реакции 7. Переходя от узла к узлу, рассматривать аналогично равновесие каждого узла. 38. Равномерное и равнопеременное движение точки Равномерным называется такое движение точки, при котором модуль скорости все время остается постоянным; следовательно, и алгебраическая величина 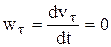 . .Равномерное прямолинейное движение является единственным движением, в котором ускорение точки все время равно нулю. Закон равномерного движения: 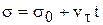 Равнопеременным называется движение точки, при котором модуль касательного ускорения остается все время постоянной: 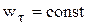 Закон равнопеременного движения точки 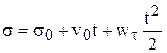 Если модуль скорости возрастает, то движение называется ускоренным, а если убывает – замедленным. |
