Предмет статики. Основные понятия и определения
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
Методы отрицательных весов, объемов и площадей являются частными случаями метода разбиений и применяются для тел с полостями (отверстия, вырезы и т.д.). В них используется идея метода разбиений, но при нахождении центра тяжести по формулам веса, объемы или площади полостей берут со знаком "-".2 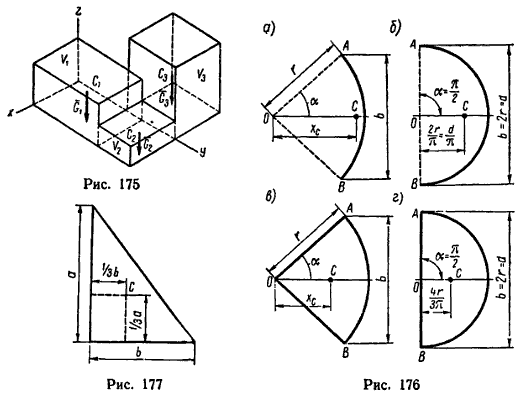 8. Центры тяжести дуги окружности и кругового сектора. Центр тяжести пирамиды. 8. Центры тяжести дуги окружности и кругового сектора. Центр тяжести пирамиды.Прямоугольник – центр тяжести на пересечении диагоналей. Треугольник – центр тяжести на пересечении медиан. Д  уга окружности: уга окружности: Круговой сектор 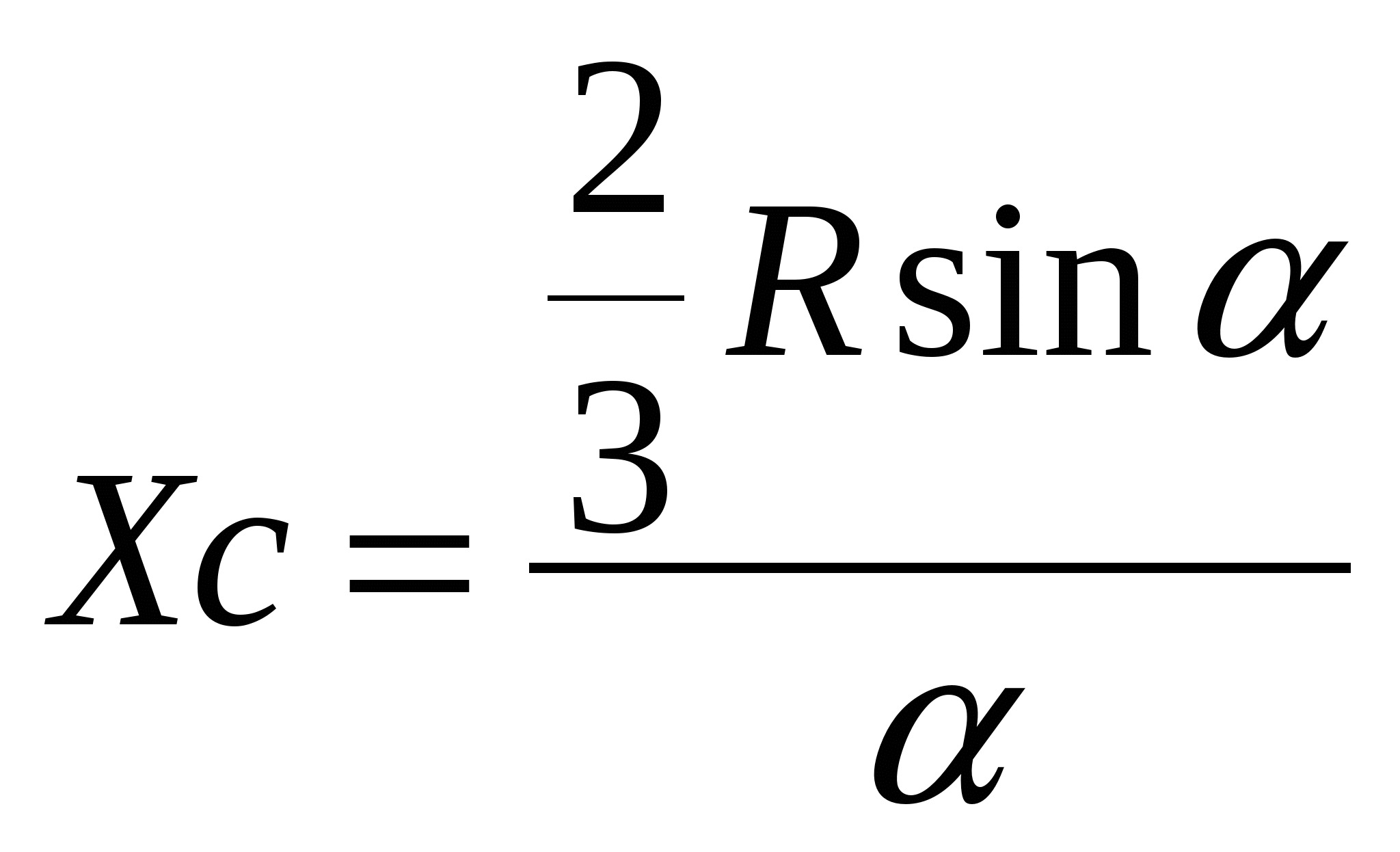 Полукруг: 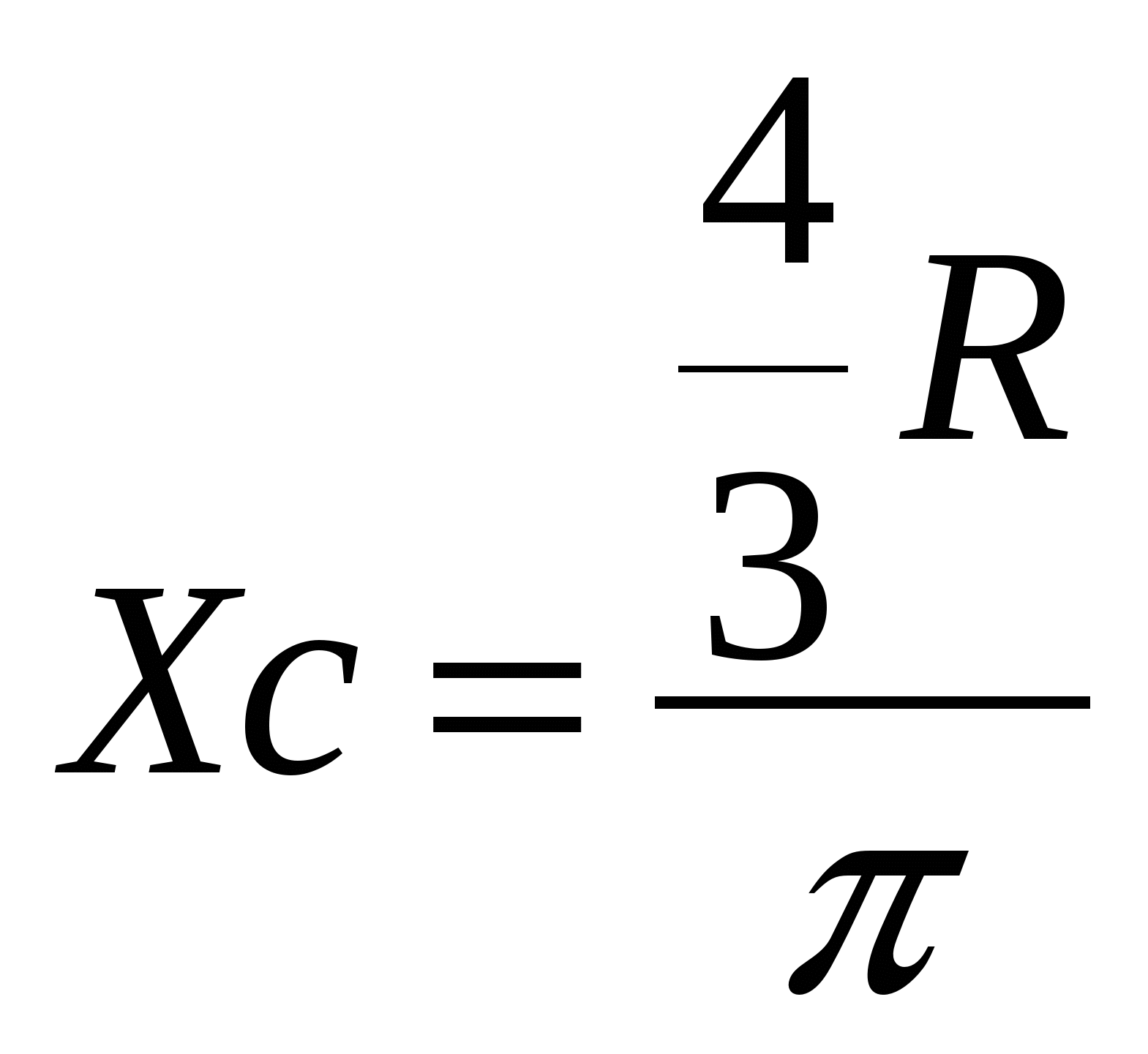 К  руговой сегмент: Для получения координаты необходимо разбивать сечение на круговой сектор и равнобедренный треугольник и затем применить метод отрицательных площадей. руговой сегмент: Для получения координаты необходимо разбивать сечение на круговой сектор и равнобедренный треугольник и затем применить метод отрицательных площадей.Конус, пирамида: Центр тяжести находится от основания пирамиды на расстоянии равной ¼ высоты. 31.Предмет кинематики. Пространство и время в классической механике. Относительность движения. Траектория движения точки. Основная задача кинематики. Кинема́тика — раздел механики, изучающий математическое описание движения идеализированных, без рассмотрения причин движения. Различают классическую кинематику, в которой пространственные и временные характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Любое движение точки или тела рассматривается относительно какой-либо системы отсчёта. Обычно систему отсчёта связывают с землёй, считая её неподвижной. Если рассматривать движение тела относительно подвижной системы отсчёта, то при расчётах необходимо учитывать движение подвижной системы отсчёта относительно неподвижной. Траекто́рия материа́льной то́чки — непрерывная линия, которую описывает точка при своём движении. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени. Также кинематика занимается изучением составных движений. Способы задания движения точки (векторный, координатный, естественный). З  адать движение точки означает задать ее положение в каждый момент времени. адать движение точки означает задать ее положение в каждый момент времени.Естественный – используется. Если известна траектория движения, уравнение движения точки по этой траектории, начало отсчёта и положительное направлении движения. К  оординатный – положение точки задаётся зависящими от времени дифференцируемыми функциями координат. X=x(t) y=y(t) z=z(t). y=f(x) – уравнение траектории. оординатный – положение точки задаётся зависящими от времени дифференцируемыми функциями координат. X=x(t) y=y(t) z=z(t). y=f(x) – уравнение траектории.Векторный – положение описывается радиус-вектором проведённым из некоторой неподвижной точки. r=r(t) уравнение движения при векторном способе. Траектори в данном случае является гадографом радиус-вектора. 33. Скорость точки при векторном способе задания движения. Положение точки задается ее радиус-вектором Скорость точки определяется как вектор Ускорение определяется как вектор 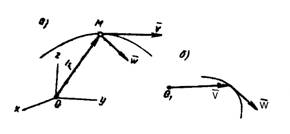 34. Ускорение точки при векторном способе задания движения. При векторном способе задания движения ускорение точки – это мера изменения скорости точки, равная производной по времени от скорости этой точки в рассматриваемой системе отсчета: 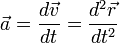 . .где a - ускорение точки, м/с2. Величина равная отношению приращения дэльта(V) вектора r к промежуточному времени дэльта(t) за который произошло это приращение называется средним ускорением точки за это время a cр.= дэльта(V)/дэльта(t). При дэльта(t) стремящимся к 0: a= dV/dt ускорение точки в данный момент времени. Ускорение всегда направлена по касательной к гадографу вектора скорости. 3 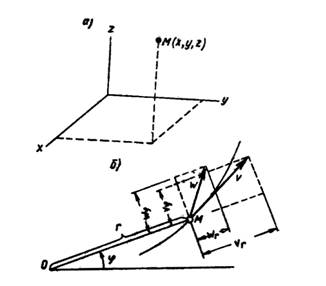 5. Скорость и ускорение при координатном способе задания движения. 5. Скорость и ускорение при координатном способе задания движения.В декартовых координатах положение точки задается ее координатами: 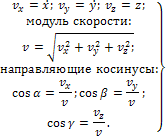 Скорость точки определяется ее проекциями на оси координат: 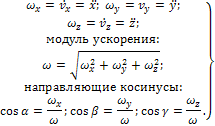 Ускорение определяется его проекциями на оси координат: 3 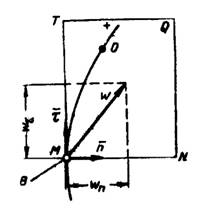 6. Скорость точки при естественном способе задания движения. 6. Скорость точки при естественном способе задания движения.а) траектория движения, т. е. линия в пространстве, с точками которой последовательно совмещается в своем движении исследуемая точка: с траекторией связана естественная система координат, показанная на рис. 3, где Q - соприкасающаяся плоскость, Т - касательная, N - главная нормаль и B - бинормаль к траектории в той ее точке, в которой находится движущаяся точка М в данный момент. 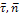 - орты осей Т и N; - орты осей Т и N;б) начало 0 и направление (+, -) отсчета расстояний вдоль траектории; в 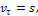 ) закон движения s=s(t), определяющий расстояние s от начала отсчета расстояний до положения точки в данный момент (дуговую координату точки). ) закон движения s=s(t), определяющий расстояние s от начала отсчета расстояний до положения точки в данный момент (дуговую координату точки).Скорость точки определяется своей проекцией на касательную: имеющий знак «+» в том случае, когда движение происходит в направлении отсчета расстояний. 37. Естественный трехгранник. Разложение ускорения по естественным осям. Касательное и нормальное ускорение. Репер или трёхгранник Френе или Френе — Серре известный также, как естественный, сопровождающий, сопутствующий — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых. Пусть γ(s) — произвольная натурально параметризованная бирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов
к кривой в данной точке. Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору Т 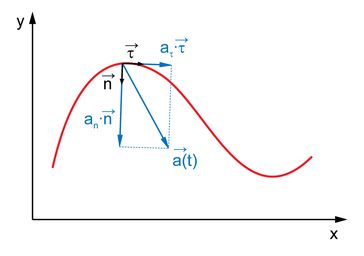 ангенциа́льное ускоре́ние — компонента ускорения, направленнаяпокасательной к траектории движения. ангенциа́льное ускоре́ние — компонента ускорения, направленнаяпокасательной к траектории движения. 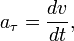 Центростремительное ускорение — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. 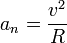 или 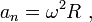 37. Частные случаи движения точки. Смысл касательного и нормального ускорения. Частные случаи движения точки: 1) Прямолинейное: радиус кривизны r= ¥(бесконечно большой) Þ аn=0, a=at. 2) Равномерное криволинейное движ-ие: v=const Þ at=0, a=an. Ускорение появляется только за счет изменения направления скорости. Закон движ-ия: s=s0+v×t, при s0=0 v=s/t. 3) Равномерное прямолинейное движ-ие: а=at=an=0. Единственное движение, где а=0. 4) Равнопеременное криволинейное движение: at=const, v=v0+at×t, . При равноускоренное движении знаки у at и v одинаковы, при равнозамедленном – разные. Тангенциальное ускорение характеризует изменение модуля скорости точки. Нормальное ускорение показывает, как меняется траектория движения точки. 39. Кинематика твердого тела. Виды движения твердого тела. Поступательное движение твердого тела. Кинематика твёрдого тела — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины. Виды движения твердого тела: 1) поступательное 2) вращательное 3) плоское или плоскопараллельное 4) сферическое 5) общий случай движения твердого тела Поступательны движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе. Теорема: Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения. 40. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения тела. Угловая скорость и угловое ускорение. Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. второй закон Ньютона для вращательного движения: 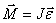 основного уравнения динамики вращательного движения: 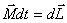 Углова́я ско́рость — векторнаявеличина, характеризующая скорость вращения тела. 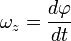 Углово́е ускоре́ние — псевдовекторнаяфизическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. 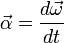 , ,41. Равномерное и равнопеременное вращение Вращение называется равномерным, если в процессе движения угловая скорость остается постоянной по модулю и по направлению, то есть, если ω=const. Закон равномерного вращения: ρ=ρ0+ω*t. Вращение называется равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению, т.е. ε=const. Закон изменения угловой скорости: ω=ω0+ε*t. Закон равнопеременного вращения: ρ=ρ0+ω0*t+ε*t2/2. 42. Определение кинематических характеристик движения точек вращающегося тела. Траектории, закон движения. Скорость и ускорение точек вращающегося тела. Основные кинематические характеристики Вращательное движение тела — его угловая скорость ω и угловое ускорение ε. Для любой точки тела, отстоящей от оси на расстоянии h, линейная скорость v = hω, касательное ускорение wτ = hω, нормальное ускорение wn = hω2 и полное ускорение 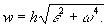 Закон вращения определяется из основного уравнения Iz ε = Mz,где Mz — вращающий момент Модуль вращательной скорости точки твердого тела равен произведению расстояния от точки до оси вращения на угловую скорость тела. 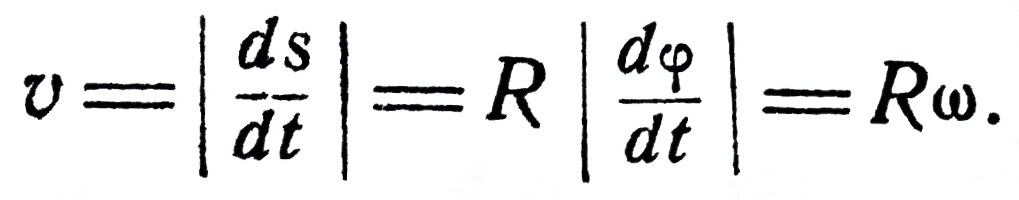 Модули вращательных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения. Модуль вращательного ускорения точки твердого тела равен произведению расстояния от точки до оси вращения на модуль углового ускорения тела. 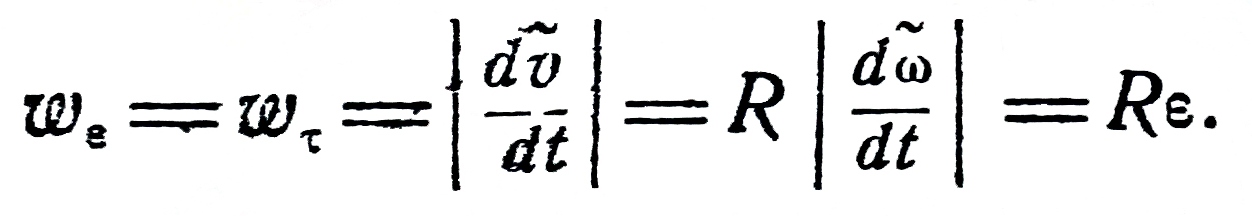 |

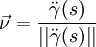 — единичный вектор главной
— единичный вектор главной