Предмет статики. Основные понятия и определения
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
Четыре случая приведения силINCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image001.gif" \* MERGEFORMATINET 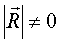 ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image002.gif" \* MERGEFORMATINET ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image002.gif" \* MERGEFORMATINET INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image001.gif" \* MERGEFORMATINET 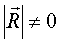 ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image003.gif" \* MERGEFORMATINET ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image003.gif" \* MERGEFORMATINET INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image004.gif" \* MERGEFORMATINET 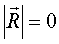 ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image005.gif" \* MERGEFORMATINET ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image005.gif" \* MERGEFORMATINET INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image004.gif" \* MERGEFORMATINET 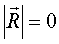 ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image006.gif" \* MERGEFORMATINET ; INCLUDEPICTURE "http://www.pppa.ru/metodika/theory/mechanics10.files/image006.gif" \* MERGEFORMATINET Уравнения центральной винтовой оси Mx - yRz + zRy = pRx, My - zRx + xRz = pRy, Mz - xRy + yRx = pRz, R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение) 20. Уравнение равновесия пространственной системы сил. Частные случаи. Условия равновесия пространственной системы сил:  Шесть уравнений: три суммы проекций сил на оси координат и три суммы моментов относительно осей координат Частные случаи:  1) Равновесие пространственной системы параллельных сил. 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы, тогда проекции сил на x и y равны 0 (Fkx=0 и Fky=0), а остаётся только Foz. А что касается моментов, то остаются только Mox и Moy, а Mozотсутствует. Пусть ось Z параллельна линиям действ силы, тогда проекции сил на x и y равны 0 (Fkx=0 и Fky=0), а остаётся только Foz. А что касается моментов, то остаются только Mox и Moy, а Mozотсутствует. 2) Равновесие плоской системы сил. Остаются ур-я Fox, Foy и момент Moz .  3) Равновесие плоской системы параллельных сил. Остаются только 2 ур-я: Foy и Moz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка. 3) Равновесие плоской системы параллельных сил. Остаются только 2 ур-я: Foy и Moz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка. 25,26,29. Центр параллельных сил. Центр тяжести твердого тела. Центр тяжести однородного объема, площади, материальной линии. Статический момент площади относительно оси. Центр параллельных сил, точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол. Координаты Центр параллельных сил определяются формулами: 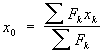 , , 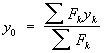 , , 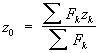 где xk, yk, zk - координаты точек приложения сил. Понятием Центр параллельных сил пользуются при отыскании координат центров тяжести тел. Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Центр тяжести различных тел: xc = (∑ Gixi) / ∑ Gi; yc = (∑ Giyi) / ∑ Gi; zc = (∑ Gizi) / ∑ Gi. ц 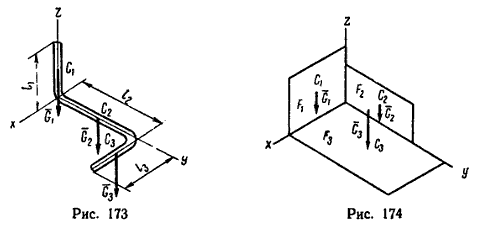 ентра тяжести фигуры, составленной из отрезков линий: ентра тяжести фигуры, составленной из отрезков линий:xc = (∑ lixi) / ∑ li; yc = (∑ liyi) / ∑ li; zc = (∑ lizi) / ∑ li. ц 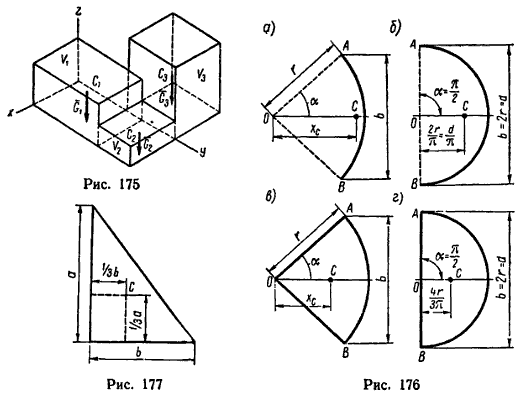 ентра тяжести фигуры, составленной из площадей: ентра тяжести фигуры, составленной из площадей: xc = (∑ Fixi) / ∑ Fi; yc = (∑ Fiyi) / ∑ Fi; zc = (∑ Fizi) / ∑ Fi. центра тяжести тела, составленного из однородных объемов: xc = (∑ Vixi) / ∑ Vi; yc = (∑ Viyi) / ∑ Vi; zc = (∑ Vizi) / ∑ Vi. С  татическим моментом Sx сечения относительно какой-либо оси х называется геометрическая характеристика, определяемая интегралом вида татическим моментом Sx сечения относительно какой-либо оси х называется геометрическая характеристика, определяемая интегралом вида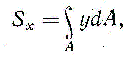 где y - расстояние от элементарной площадки dA до оси x. 27. Методы нахождения центра тяжести (симметрии, разбиения, дополнения). Метод интегрирования является универсальным. Он пригоден для определения координат центров тяжести однородных и неоднородных тел любой формы. Метод разбиения – применяется, когда однородное тело можно разбить на части, положения центров тяжести которых известны или легко определяются. В неоднородном теле эти части должны иметь еще и одинаковый удельный вес во всех их точках. После разбиения положение центра тяжести всего тела находят, используя дискретные формулы для определения координат центра тяжести. Метод симметрии применяется только для однородных т  ел. Сформулируем три правила метода. ел. Сформулируем три правила метода.1. имеет плоскость симметрии - центр тяжести лежит в этой плоскости. 2. имеет ось симметрии- центр тяжести находится на этой оси. 3. имеет центр симметрии- центр тяжести находится в этой точке. |
