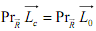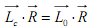Предмет статики. Основные понятия и определения
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=MB(F). Таким образом, лемма о параллельном переносе силы доказана.
Статика – раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов. Равновесие – такое механическое состояние тела, при котором оно находится в состоянии покоя или движется прямолинейно и равномерно относительно выбранной инерциальной системы отсчёта. Все тела в природе взаимодействуют между собой и с окружающей средой. Сила – векторная величина, характеризующаяся величиной (модулем силы), направлением и точкой приложения. Система тел – совокупность тел, каким-либо образом связанных между собой. Внутренние силы – силы, с которыми тела данной системы взаимодействуют друг с другом. Внешние силы – силы, с которыми тела, не входящие в систему, взаимодействуют с телами данной системы. Равнодействующая сила – это сила, равная эквивалентной системе сил по своему действию. Система сходящихся сил – это такая система сил, линии действия которой пересекаются в одной точке. Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. В механике, степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел. Равновесие механической системы – состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта. Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называется эквивалентными. Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой. Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. Твердое тело, свобода движения которого ограничена связями, называется несвободным. 2.Аксиомы статики 1) Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил. 2) О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению. 3) О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны. 4) О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах. 5) Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания. 6) Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей. Классификация силовых систем: свободная, несвободная Классификация сил: активные и реакции связей либо внешние и внутренние 3. Связи и их реакции. Аксиома связей. Основные виды связей. Тело называется свободным, если его перемещения в пространстве с течением времени ничем не ограничены. В любом другом случае тело является несвободным. Связи – ограничения, налагаемые на свободу любого несвободного тела. Силы, с которыми связи действуют на данное тело, называются реакциями связей. Аксиома связей: Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей. Виды связей:
  5. Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей. Сходящимися называются силы, линии действия(л.д.) которых пересекаются в одной точке. Если у такой системы сил л.д. расположены в одной плоскости, то она называется плоской системой сходящихся сил. В любом другом случае система сходящихся сил пространственная. Равнодействующая сходящихся сил равна геометрической сумме этих сил и приложена в точке их пересечения Геометрический способ: Теорема: любая система сходящихся сил приводится к равнодействующей, равной геометрической сумме составляющих сил и приложенных в точках пересечения линий их действия. Сложность данного подхода в сложности геометрических построений. Для упрощения построений сложим геометрически силы следующим образом: конец предыдущей силы должен совпадать с началом следующего, а линии действия сил должны быть параллельны заданным. Замыкающая, полученная таким образом, и будет являться вектором равнодействующей, причем он должен быть направлен то начала к концу. Аналитический способ: Проекцией силы на ось называется направленный отрезок, заключенный между перпендикулярами, проведенными к соответствующей оси из начала к концу вектора силы. В случае пространственной системы сил используется метод двойного проецирования: сначала сила проецируется на плоскость, а затем определяются проекции полученной проекции на осях координат.  6. Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Геометрическое условие равновесия: Силовой многоугольник должен быть замкнут, т.е. конец последнего вектора должен совпадать с началом первого. Аналитическое условие равновесия: Равенство 0 проекций равнодействующей на оси координат (Rx=0, Ry=0, Rz=0). Для равновесия тел, находящихся под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая была равна 0 (R=0). Для равновесия тела, находящегося в системе сходящихся сил, необходимо и достаточно, чтобы были равны 0 алгебраические суммы проекций всех сил на оси произвольно выбранных систем координат.  11.Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно центра. Векторный момент силы относительно центра – векторное произведение радиус-вектора точи приложения силы относительно центра на вектор силы. Теорема Вариньона: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). Алгебраическим моментом силы F относительно некоторого центра называется взятое со знаком + или - произведение модуля силы F на плечо (кротчайшее расстояние от точки до линии действия силы). Момент положителен, если сила стремиться вращать плоскость действия против часовой стрелки и наоборот. (M=F*h) Но при этом h можно выразить через радиус-вектор r (h=r*sin α), тогда M = F*r*sin α = (F x r). Получаем, что векторный момент силы относительно точки – векторная величина. 12. Момент силы относительно оси. Аналитическое выражение момента силы относительно оси. М 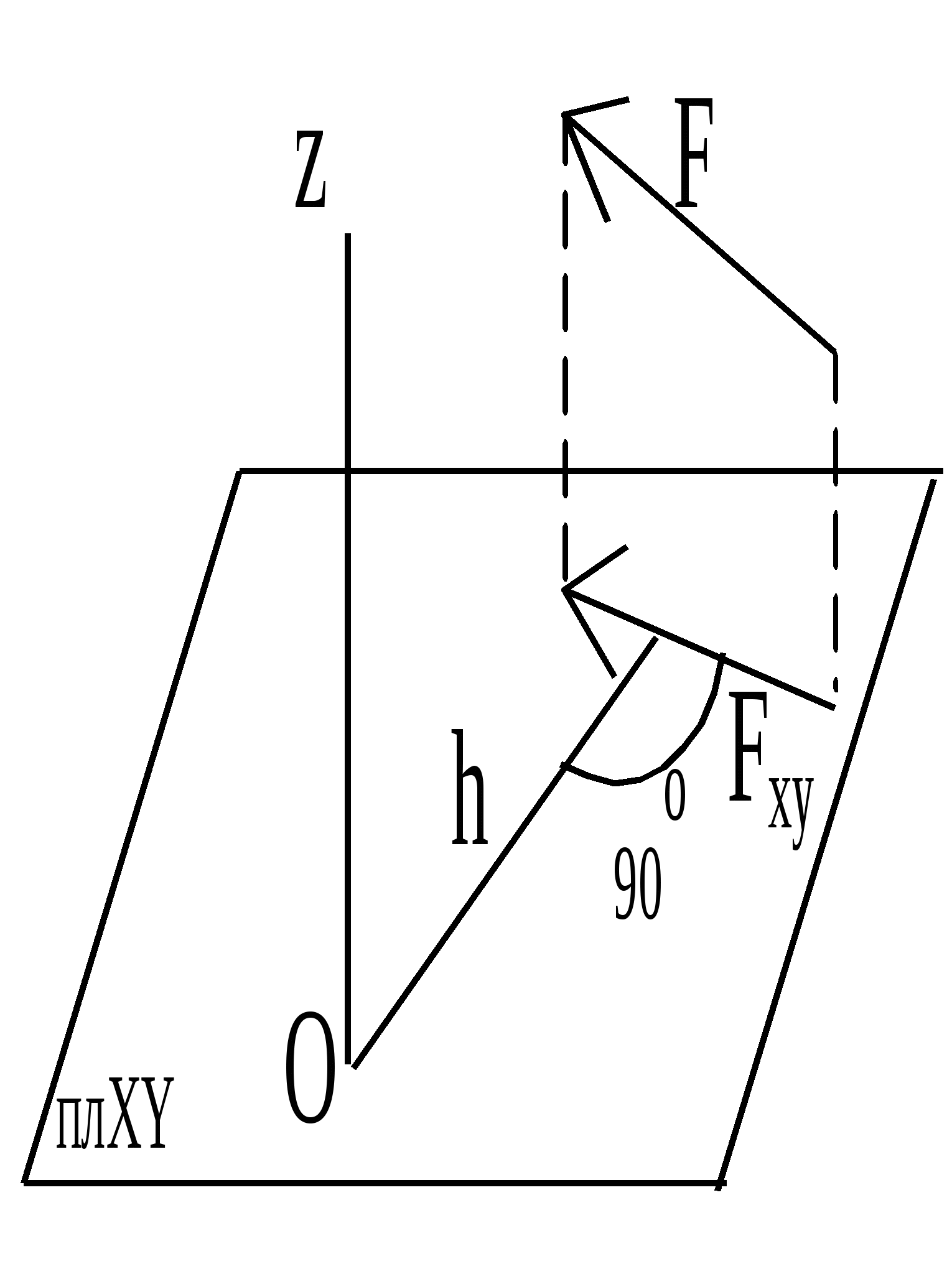 оментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. оментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси. Момент силы относительно оси равен 0 в двух случаях:
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0. 13. Связь между моментом силы относительно оси и векторным моментом силы относительно точки. Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось. 9. Сложение параллельных сил. Равнодействующая двух параллельных сил, направленных в одну сторону равна алгебраической сумме модулей составляющих сил. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Две параллельные, противоположно направленные силы, не равные по модулю, эквиваленты равнодействующей, модуль которой равен разности модулей слагаемых сил и направлены в сторону большей силы. Линия действия равнодействующей делит отрезок, заключённый между точками приложения сил внутренним образом на части, обратно пропорциональные модулям этих сил. Если модули противоположно направленных сил равны, то такая система не имеет равнодействующей, она сообщает свободному телу вращательное движение и называется парой сил. 9. Пара сил. Векторный момент пары сил. Алгебраический момент пары сил. Пара сил – совокупность двух противоположно направленных равных по модулю параллельных сил, действующих по несовпадающим линиям действия. Плоскость, в которой действует пара сил, называется плоскостью действия пары. Момент пары сил не зависит от выбора центра привидения, а определяется лишь модулями сил и расстоянием между л.д. – плечом пары. Векторный момент пары сил – вектор, равный векторному произведению радиус-вектора ρ, соединяющий точки приложения сил на вектор силы и направленный перпендикулярно плоскости действия пары сил таким образом, чтобы, смотря ему навстречу, пара сил стремилась поворачивать плоскость действия против часовой стрелки. Алгебраический момент пары сил равен произведению модуля одной из сил, составляющих пару, на плечо пары и имеет знак в соответствии с правилом знаков для момента силы. 10. Свойства пар сил. Эквивалентность пар. Теоремы об эквивалентности пар. Свойства пар сил:
Две пары сил называются эквивалентными, если они имеют геометрически равные моменты. Поэтому пара сил характеризуется при решении задач лишь моментом пары и обозначается m=M0(F1;F2). т-мы: (1)Две пары сил произвольно расположенных в пространстве эквивалентны одной паре сил с моментом, равным геометрической сумме моментов слагаемых пар. (2) еси на тело действует произвольная система пар, то ветор момента результирующей пары равен векторной сумме моментов составляющих пар. (3)Если все пары сил расположены перпендикулярно одной плоскости, то вектора моментов пар направлены перпендикулярно этой плоскости в ту или иную сторону, поэтому моменты пар можно складывать алгебраически. (4) для равновесия тела, находящегося под действием системы произвольно расположенной в пространстве пар необходимо и достаточно, чтобы момент результирующей пары был равен 0. 10. Сложение пар сил. Условие равновесия системы пар сил. Теорема о сложении пар сил: Две пары сил, произвольно расположенные в пространстве, эквивалентны одной паре с моментом равным геометрической сумме моментов слагаемых пар. Если на тело действует произвольная система (М1,М2,…,Мn) пар, то вектор момента результирующей пары равен векторной сумме моментов, составляющих пары. M=M1+M2+…+Mn=ΣMk (сверху векторы) Если две пары сил расположены в одной плоскости, то векторы моментов пар направлены перпендикулярно этой плоскости в ту или иную стороны. Поэтому моменты пар можно складывать алгебраически. M=M1+M2+…+Mn=ΣMk Условие равновесия системы пар сил: Для равновесия тела, находящегося под действием системы произвольно расположенных в пространстве пар, необходимо и достаточно, чтобы момент результирующей (эквивалентной) пары был равен 0. M=ΣMk=0 В случае, если все пары сил расположены в одной плоскости (или в параллельных плоскостях), то для равновесия необходимо равенство 0 алгебраической суммы моментов составляющих пар. 15. Основная лемма статики о параллельном переносе силы. Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F. Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F |
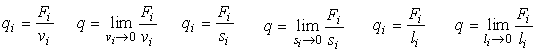 |
q1 - средняя интенсивность
величина и координаты точки приложения равнодействующей параллельных распределенных с интенсивностью меняющейся по закону:
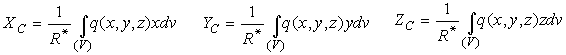 | |
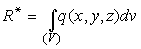 | |
Равнодействующая параллельных распределенных сил, перпендикулярных участку поверхности, равна по величине объему фигуры, занимаемой силами, проходит через центр тяжести этой фигуры параллельно распределенным силам в сторону их действия.
Равнодействующая параллельных распределенных сил, перпендикулярных отрезку линии, равна по величине площади фигуры, занимаемой силами, проходит через центр тяжести этой фигуры параллельно распределенным силам в сторону их действия.
Р
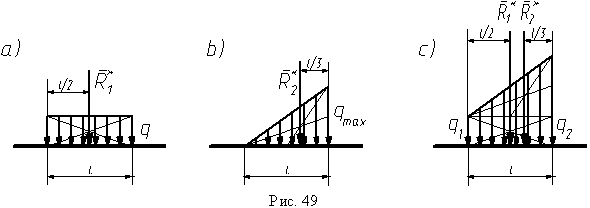 авнодействующая R1* сил с постоянной интенсивностью q равна по модулю площади прямоугольника, занимаемого силами R1* = ql , проходит параллельно силам через его центр тяжести (точка пересечения диагоналей прямоугольника) и приложена в середине отрезка длиной l.
авнодействующая R1* сил с постоянной интенсивностью q равна по модулю площади прямоугольника, занимаемого силами R1* = ql , проходит параллельно силам через его центр тяжести (точка пересечения диагоналей прямоугольника) и приложена в середине отрезка длиной l. 
Равнодействующая R2* сил с интенсивностью, меняющейся по линейному закону от 0 доqmax, по величине равна уже площади треугольника R2* = qmaxl/2 , проходит через точку пересечения его медиан и приложена к точке отрезка на расстоянии l/3 от наибольшей силы.
Комбинируя два простейших случая, можно приводить силы с более сложным законом распределения.
С
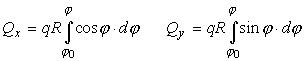 ходящиеся распределенные силы:
ходящиеся распределенные силы:
Qx = 2qR sinα = qAB; Qy = 0 Q = Qx
22. Трение скольжения. Законы трения. Угол и конус трения. Условия равновесия тел на шероховатой поверхности.
Сила трения, возникающая при скольжении одного тела по поверхности другого называется силой трения скольжения.
СТС меньше предельного значения силы трения покоя Fсц, т.к. fn чуть меньше коэффициента трения скольжения (fn˂f).
F зависит только от материалов трущихся поверхностей:
0,01…0,02 – сталь по льду
0,2…0,5 – сталь по стали
0,4…0,6 – резина по асфальту
0,8 – резина по асфальту
Предельное значение силы трения определяется произведением коэффициентов трения скольжения на модуль норм реакции опорной поверхности.
Fтр.макс.=fN – используется лишь в том случае, если известно, что наступает предельное состояния равновесия;
Во всех остальных случаях сила трения определяется из уравнения равновесия.
Законы:
(1)сила трения всегда направлена противоположно направленному движению тела. (2)Величина силы трения не зависит от площади соприкасающихся поверхностей. (3) Величинв силы трения зависит от состояния и материала трущихся поверхностей, а также наличия и вида смазки. (4) Предельное значение силы трения определяется по ф-ле Fтр.макс.=fN
Угол трения – угол между полной реакцией опорной плоскости R и нормальной реакцией N.
Геометрическое место возможных направлений предельной реакции R образует коническую поверхность – конус трения.
23. Угол и конус трения. Условия равновесия тела на шероховатой поверхности
При действии силы трения на твердое тело полная реакция отклонения от нормальной поверхности на угол ρ, которая при выходе из состояния покоя принимается следующее значение и называется углом трения, tg которого определяется по следующей формуле: tg ρ=Fтр/N.
Конусом трения называется конус, описывающий полную реакцию вокруг направления нормальной реакции. Если коэффициент трения скольжения будет одинаковым во всех направлениях, то эта реакция описывает круговой конус.
24. Трение качения — сопротивление движению, возникающее при перекатывании тел друг по другу. Как правило, величина трения качения гораздо меньше величины трения скольжения, и потому качение является распространенным видом движения в технике.
Т
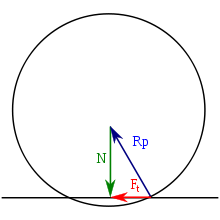 рение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.
рение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.Сила трения
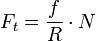
f— коэффициент трения качения,
имеющий размерность длины
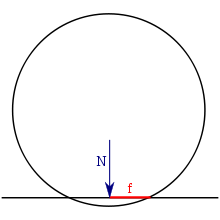
Момент сил трения качения
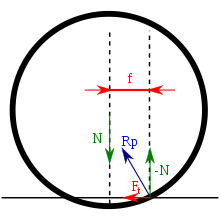
Коэффициент трения качения
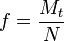
21. Расчет плоских ферм. Классификация ферм. Методы расчета плоских ферм. Леммы о нулевых стержнях.
Фе́рма в строительной механике стержневая система, остающаяся геометрически неизменяемой после замены её жёстких узлов шарнирными. Ферма, как и балка, работает на изгиб. Фермы образуются из прямолинейных стержней, соединенных в узлах.
1. Характер очертания внешнего контура: параллельные пояса, ломаные пояса, полигональные пояса, треугольные пояса.
2. Тип решётки: треугольная, раскосая, полураскосая, ромбическая.
3. Тип опирания: балочный, арочный, консольный, балочно-консольный.
4. Назначение: стропильные, мостовые, крановые, башенные.
5. Материал исполнения: деревянные, металлические, железобетонные, из полимерных материалов.
Методы расчета плоских ферм:
М
 етод вырезания углов- удобно использовать, когда надо найти усилия во всех стержнях фермы. Сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов, определению усилий в стержнях фермы.
етод вырезания углов- удобно использовать, когда надо найти усилия во всех стержнях фермы. Сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов, определению усилий в стержнях фермы.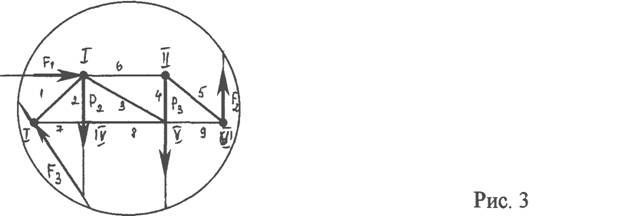
Построение диаграммы Максвелла-Кремоны - графический способ расчета усилий в стержнях фермы. Заключается в построении силовых многоугольников,
построенных для всех узлов фермы, в один чертеж так, чтобы ни одно из усилий не повторялось дважды.

Метод сечений (методом Риттера)- удобно пользоваться для определения усилий в отдельных стержнях
фермы, например, для проверочных расчетов.
Нулевыми называются стержни усилия в которых равны нулю. Нулевые стержни могут быть выявлены на этапе предварительного анализа, и это существенно может упростить последующие расчеты.
Признаки определения нулевых стержней:
1. Если к узлу с двумя стержнями, не лежащими, на одной прямой, не приложена внешняя нагрузка, то усилия в них равны нулю.
2. Если в узле сходятся три стержня, две из которых лежат на одной прямой и нагрузка в узле отсутствует, то в третьем стержне, расположенном под углом к этой прямой, усилие равно нулю.
3. Если в узле сходятся два стержня, а нагрузка направлена вдоль оси одного из них, то усилие на другой равен нулю.
25. Случаи приведения пространственной системы сил к простейшему виду.
В зависимости от соотношения R0* и М0* возможны следующие случаи приведения:1) R0*=0 и М0*=0 – система сил находится в равновесии.2) R0*≠0 и М0*=0 – система сил приводится к равнодействующей, равной главному вектору, л.д. которой проходит через центр приведения (поступательное движение)
3) R0*=0 и М0*≠0 – система сил приводится к паре сил с моментом равным главному моменту с л.д. проходящей через центр приведения (вращательное движение)
4) R0*≠0 и М0*≠0 – система сил приводится к равнодействующей, равной главному вектору с л.д. проходящей через центр приведения (R0* перпендикулярно М0*) (плоско-параллельное движение)
5) R0*≠0 и М0*≠0 (R* параллельно М*) – система сил сводится к главному вектору и главному моменту с л.д. проходящими через центр приведения (винтовое движение)6) R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение)
Центр параллельных сил – точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол.
17. Приведение системы сил к динаме. Уравнение центральной оси.

 есткая заделка
есткая заделка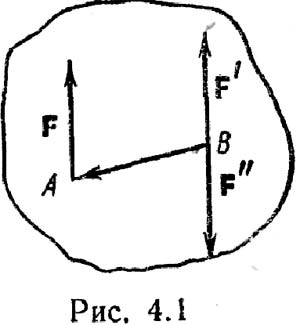

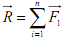 елу, к центру 0. Тогда получаем эквивалентную систему, которая характеризуется главным вектором и главным моментом
елу, к центру 0. Тогда получаем эквивалентную систему, которая характеризуется главным вектором и главным моментом 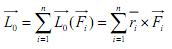
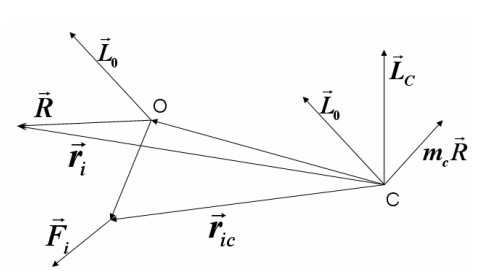

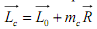 лавный вектор пространственной системы сил не изменяется при перемене центра приведения, т.е. он представляет собой статический инвариант пространственной системы сил по отношению к изменению центра приведения.
лавный вектор пространственной системы сил не изменяется при перемене центра приведения, т.е. он представляет собой статический инвариант пространственной системы сил по отношению к изменению центра приведения.