1
|
Предмет и основные понятия ТВ. Алгебра событий.
|
Предмет теории вероятностей.
Наблюдаемые нами явления (события) можно разделить на 3 вида: достоверные, невозможные и случайные.
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Полной группой случайных событий называется группа всевозможных, равновозможных и единственно-возможных событий.
|
2
|
Определение вероятности события.
|
Классическое определение вероятности (определяет количественные шансы наступления случайного события)
Вероятностью случайного события А называется отношение числа благоприятных случаев к общему числу всевозможных, равновозможных и единственно-возможных случаев.
Статистическое определение вероятности (экспериментальное, опытное определение).
Статистической вероятностью события А называется отношение числа благоприятствующих исходов опытов к общему числу проведенных опытов (испытаний).
|
3
|
Комбинаторика.
|
Комбинаторика – раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка).
Правило умножения. Пусть объект 𝐴 можно выбрать 𝑛 способами и после каждого такого выбора объект 𝐵 можно выбрать 𝑚𝑚 способами. Тогда выбор пары (𝐴, 𝐵) можно осуществить 𝑛𝑛𝑛𝑛 способами.
Правило сложения. Пусть некоторый объект 𝐴 можно выбрать 𝑛𝑛 различными способами, а другой объект 𝐵 можно выбрать 𝑚𝑚 способами. Тогда существует 𝑛 + 𝑚 способов выбрать либо объект 𝐴, либо объект 𝐵.
Правило вычитания. Пусть существует 𝑛𝑛 различных исходов некоторого события, среди которых некоторым свойством обладают 𝑚 исходов. Тогда существует 𝑛𝑛 − 𝑚𝑚 исходов, не обладающих этим свойством.
Перестановки без повторений. Пусть дано 𝑛 различных объектов, которые надо расставить на 𝑛𝑛 мест в определенной последовательности. Это можно сделать 𝑃𝑛 = 𝑛! различными способами.
Перестановки с повторениями. Пусть дано 𝑛1 одинаковых объектов первого вида, 𝑛2 – второго вида, и т.д., и их все надо расставить в определенной последовательности. Это можно сделать 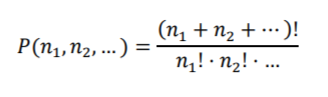
различными способами
Размещения без повторений. Пусть дано 𝑛𝑛 различных объектов, некоторые из которых надо расставить на 𝑚𝑚 мест, при этом каждый объект можно использовать только один раз. Это можно сделать 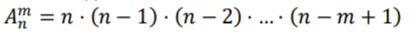
различными способами.
Размещения с повторениями. Пусть дано 𝑛𝑛 различных объектов, некоторые из которых надо расставить на 𝑚𝑚 мест, при этом каждый объект можно использовать неограниченное количество раз. Это можно сделать
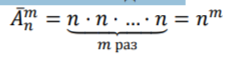
Сочетания без повторений. Пусть дано 𝑛𝑛 различных объектов, среди которых надо выбрать группу из 𝑚𝑚 объектов. Это можно сделать
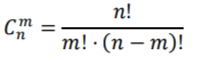
|
4
|
Основные теоремы ТВ.
|
|
5
|
Формулы полной вероятности и гипотез.
|

|
6
|
Повторные независимые испытания (формула Бернулли). Наивероятнейшее число наступления события в независимых испытаниях.
|
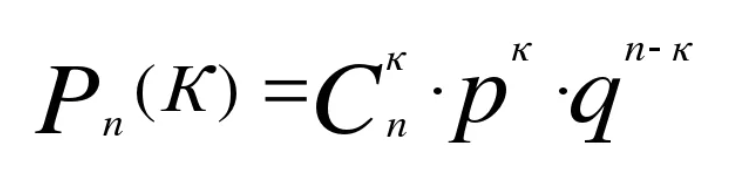 
|
7
|
Локальная теорема Муавра-Лапласа.
|

|
8
|
Интегральная теорема Муавра-Лапласа.
|

|
9
|
Пуассоновское приближение.
|

|
10
|
Случайные величины и их виды.
|
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
Случайные величины обозначаются: X, Y, Z,... Значения, которые они принимают: x,y,z.
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
|
11
|
Закон распределения дискретной случайной величины.
|
Дискретную случайную величину Х можно характеризовать законом распределения.
Закон распределения дискретной случайной величины- это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.

|
12
|
Основные законы распределения дискретных случайных величин.
|
Биномиальный закон распределения
е. Дискретная случайная величина Х имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0,1,2,…,m,…,n с вероятностями
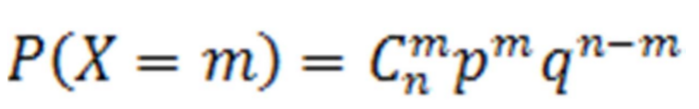
Закон распределения Пуассона
Геометрическое распределение
Равномерный закон распределения
Показательный(экспоненциальный) закон распределения
Нормальны закон распределения
|
13
|
Мат. ожидание дискретной случайной величины и его свойства.
|
Математическое ожидание дискретной случайной величины Х- это величина, где xi- значения случайной величины, pi- их вероятности, n- число возможных значений случайной величины.
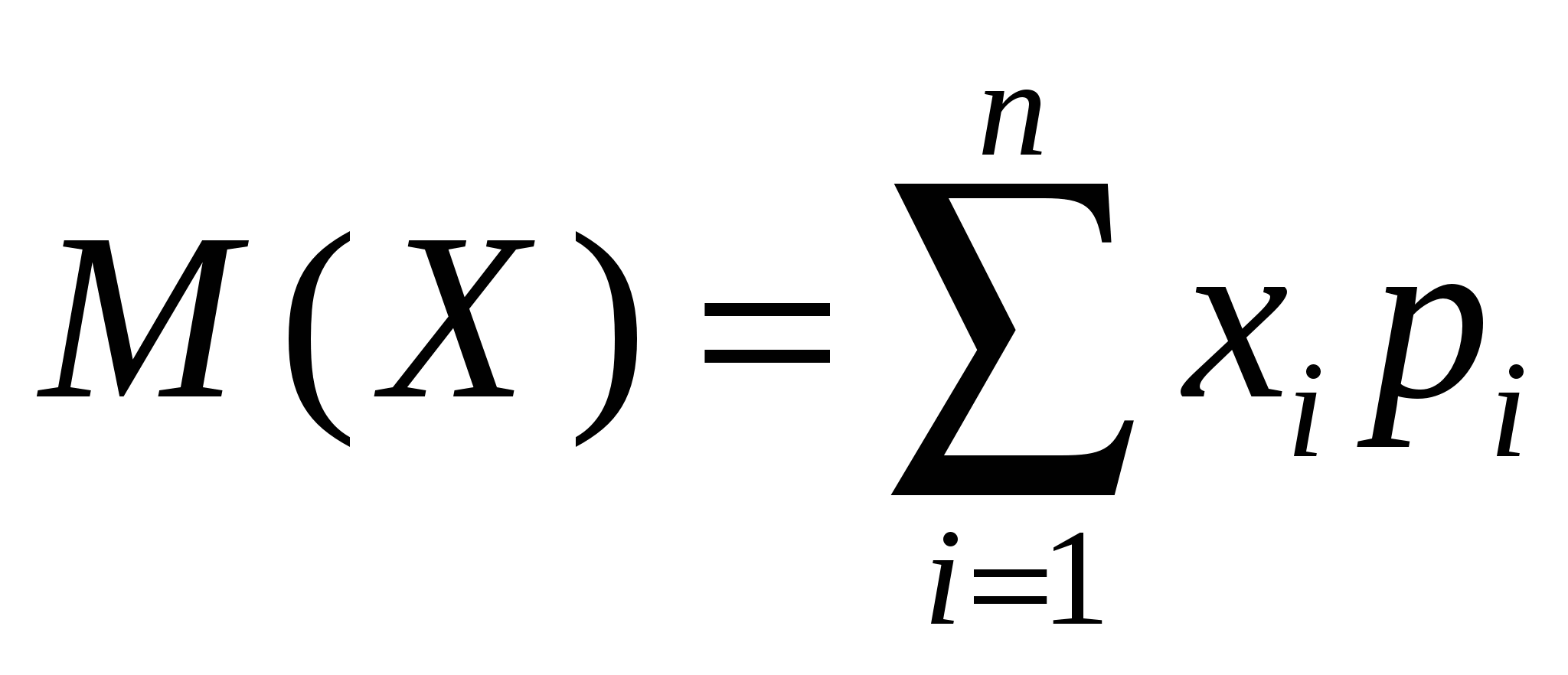
|
14
|
Математическое ожидание основных законов распределения ДСВ
|
|
15
|
Дисперсия ДСВ и её свойства.
|

Свойство 1.
Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Свойство 2.
Дисперсия константы равна нулю:
Свойство 3.
Постоянный множитель выносится из-под знака дисперсии в квадрате:
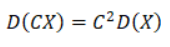
Свойство 4.
Дисперсия суммы случайных величин:
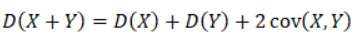
где cov(X, Y) – ковариация случайных величин X и Y
|
16
|
Дисперсия основных законов ДСВ
|
|
17
|
Производящие функции ДСВ.
|
Определение. Производящей функцией дискретной целочисленной случайной величины 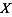 с законом распределения с законом распределения 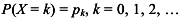 называется функция, заданная степенным рядом называется функция, заданная степенным рядом
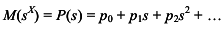
Теорема 4.4. Производящая функция суммы независимых случайных величин 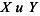 равна произведению производящих функций слагаемых равна произведению производящих функций слагаемых
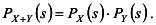
Доказательство. Имеем по определению
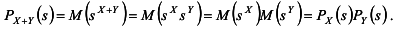
|
18
|
Вероятностный анализ алгоритмов
|
|
19
|
Одинаково распределенные взаимно-независимые случайные величины
|
Случайные величины называют одинаково распределенными, если они имеют одинаковые законы распределения. Поэтому у них совпадают числовые характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Пусть X1, X2,…, Xn одинаково распределенные, взаимно независимые дискретные случайные величины, тогда: M(X1) = M(X2) = …= M(Xn) = M(X), D(X1) = D(X2) = …= D(Xn) = D(X).
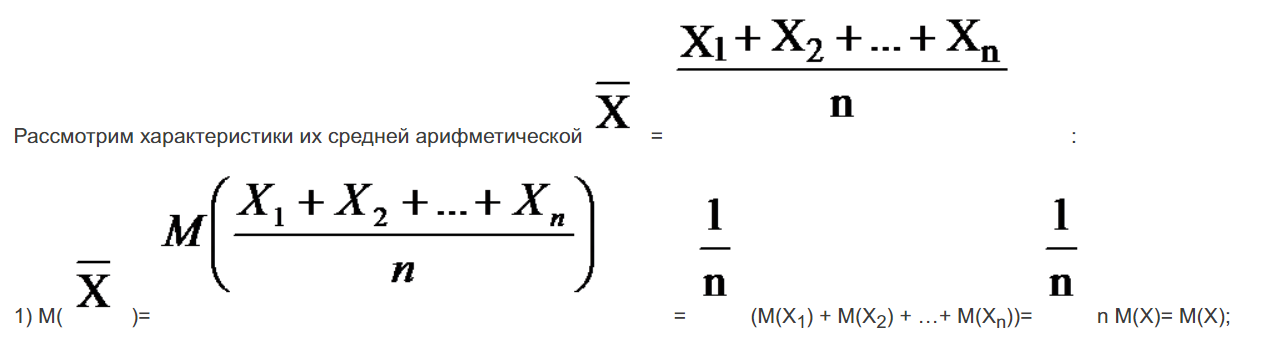
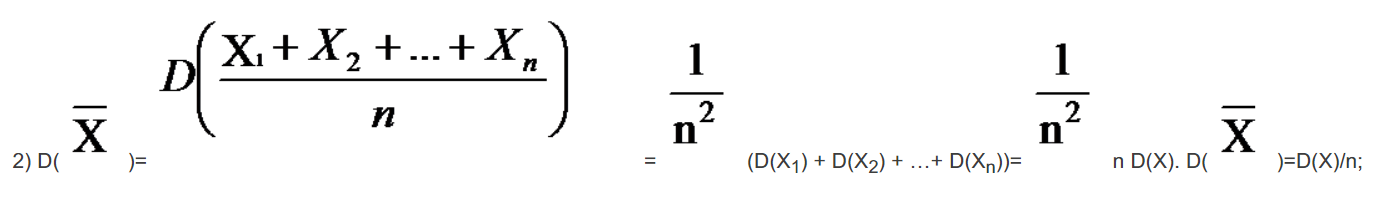
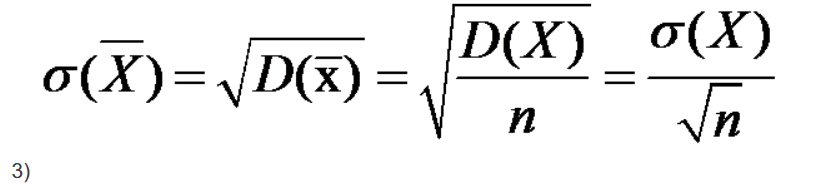
- стандартное отклонение среднего арифметического взаимно независимых одинаково распределенных случайных величин.
4) Дисперсияотносительной частоты 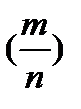 появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q=1-p; m - число появлений события А в серии из n испытаний), равна D появления события А в n независимых испытаниях (в каждом из которых событие А появляется с вероятностью равной р, и не появляется с вероятностью q=1-p; m - число появлений события А в серии из n испытаний), равна D 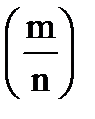 = = 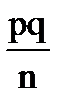 . .
|
20
|
Интегральная функция распределения вероятностей и её свойства. Дифференциальная функция распределения вероятностей и её свойства.
|
Если X - случайная величина, то функция F(x) - интегральная функция распределения вероятностей
Свойства F(x):
1. Интегральная функция распределения принимает значения от 0 до 1.
2. F(x) - неубывающая функция, то есть F(x2) 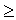 F(x1), если x2 > x1. F(x1), если x2 > x1.
3. Вероятность того, что случайная величины X примет значение, заключенное в интервале (а, b) равна приращению интегральной функции распределения на этом интервале:
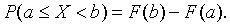
4. Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то:
F(x) = 0, если x 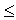 a, a,
F(x) = 1, если x 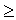 b b
Дифференциальной функцией распределения вероятностей называют первую производную от функции распределения:

Часто вместо термина «дифференциальная функция» используют термин «плотность».
Свойства 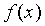 : :
1. 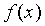 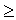 0 0
2. 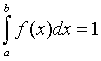 , если все возможные значения X принадлежат интервалу (a, b) , если все возможные значения X принадлежат интервалу (a, b)
|
21
|
Числовые характеристики непрерывных случайных величин
|
Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то математическое ожидание непрерывной случайной величины X: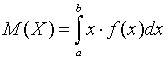
Матаматическое ожидание - определяет среднее значение случайной величины Х
Дисперсия - отклонение случайной величины Х от среднего значения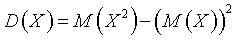 , ,
где 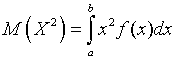
Cреднеквадратическое отклонение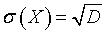
|
22
|
Равномерное распределение.
|

|
23
|
Показательное распределение.
|
Плотность распределения величины X с экспоненциальным законом распределения задается формулой:
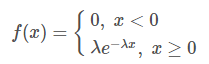
Функция распределения величины X:
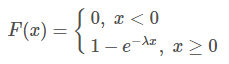
Здесь λ - единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: M(X)=1/λ; D(X)=1/λ2.
Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр λ описывает среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.
|
24
|
Нормальное распределение. Вероятность заданного отклонения. Правило 3х сигм.
|
О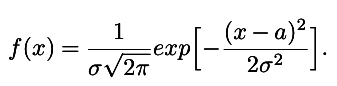 бщим нормальным распределением вероя тностей непрерывной случайной величины бщим нормальным распределением вероя тностей непрерывной случайной величины 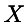 называется распределение с плотностью называется распределение с плотностью
Нормальное распределение задается двумя параметрами: 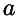 и и 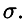
вероятность того, что нормально распределенная случайная величина 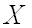 примет значение, принадлежащее интервалу примет значение, принадлежащее интервалу 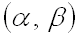 , равна: , равна:
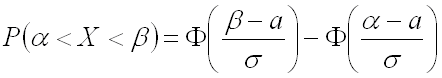 , ,
где 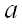 – математическое ожидание, – математическое ожидание, 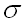 – среднее квадратическое отклонение данной случайной величины. – среднее квадратическое отклонение данной случайной величины.
|
25
|
Понятие многомерной случайной величины и способы её задания на примере двумерной дискретной величины.
|
Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин обозначать . Такая система называется также многомерной случайной величиной. При изучении системы случайных величин недостаточно изучить отдельно случайные величины, составляющие систему, а необходимо учитывать связи или зависимости между этими величинами.
При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин можно рассматривать как случайную точку на плоскости с координатами и или как случайный вектор на плоскости со случайными составляющими и . По аналогии систему случайных величин можно рассматривать как случайную точку в -мерном пространстве или как n-мерный случайный вектор.
|
26
|
Интегральная функция двумерной СВ. Вероятность попадания двумерной СВ в полуполосу и прямоугольник.
|
Интегральной функцией распределения двумерной случайной величины (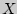 , , 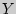 ) называется вероятность совместного выполнения двух неравенств: ) называется вероятность совместного выполнения двух неравенств:
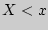 и и 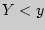 : :
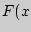 , , 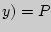 { {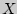 < < 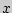 , ,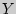 < < 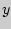 } }
и геометрически определяет вероятность попадания случайной точки (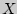 , ,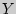 ) в бесконечный квадрат с вершиной в точке ( ) в бесконечный квадрат с вершиной в точке (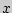 , , 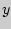 ), лежащей левее и ниже ее. ), лежащей левее и ниже ее.
|
27
|
Независимость СВ и их числовые характеристики. Коэффициент корреляции и его свойства.
|
Коэффициент корреляции Пирсона - это ковариация двух переменных, деленная на произведение их стандартных отклонений. Форма определения включает «момент продукта», то есть среднее значение (первый момент о происхождении) произведения случайных величин, скорректированных на среднее значение; отсюда и модификатор product-moment в названии.
Коэффициент корреляции Пирсона, когда он применяется к совокупности , обычно обозначается греческой буквой ρ (ро) и может называться коэффициентом корреляции совокупности или коэффициентом корреляции Пирсона совокупности . Для пары случайных величин формула ρ имеет следующий вид:
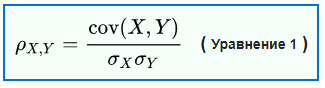

|
28
|
Закон распределения функции СВ.
|
Закон распределения СВ - это отношение, устанавливающее связь между возможными значениями СВ и вероятностями, с которыми принимаются эти значения. Закон распределения полностью характеризует СВ.

|
29
|
Композиция распределений
|
Композицией распределений называется алгоритм (формула), по которому можно получить закон распределения суммы случайных величин на основе совместного закона распределения случайных величин
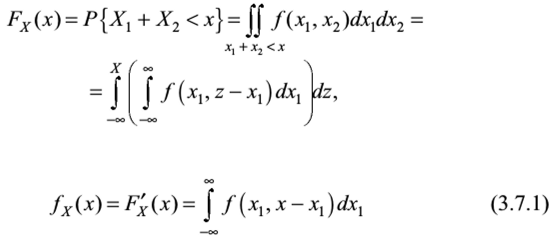
|
30
|
Распределение Хи квадрат Пирсона, t – Стьюдента, F – Фишера.
|
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
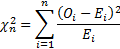
Это и есть статистика для критерия Хи-квадратПирсона.
Критерий позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».
При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.
Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.


Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:

|
31
|
Сущность закона больших чисел
|
Закон больших чисел — основной закон в теории вероятностей, который утверждает, что среднее значение случайных величин из заданного распределения близко к теоретическому среднему значению (математическое ожидание) этого распределения[1]. Закон также можно трактовать так: при увеличении числа испытаний частота появления события будет все меньше отличаться от вероятности его появления.
|
32
|
Неравенство Чебышева. Теорема Чебышева
|
 
|
33
|
Характеристическая функция. Понятие о центральной предельной теореме.
|
Пусть есть случайная величина {\displaystyle X}Х с распределением {\displaystyle \mathbb {P} ^{X}}PX. Тогда характеристическая функция задаётся формулой: 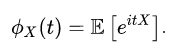
Пользуясь формулами для вычисления математического ожидания, определение характеристической функции можно переписать в виде:
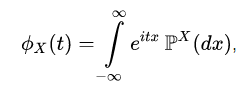
то есть характеристическая функция — это обратное преобразование Фурье распределения случайной величины.
Если случайная величина {\displaystyle X}X принимает значения в произвольном гильбертовом пространстве {\displaystyle {\mathcal {H}}}HH, то её характеристическая функция имеет вид:
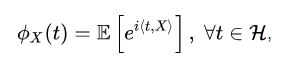
где {\displaystyle \langle \cdot ,\cdot \rangle }{{{*,*} обозначает скалярное произведение в H.
ЦПТ:

|
34
|
Цепи Маркова. Понятие о случайных процессах.
|
Цепи Маркова — это последовательность событий или действий, где каждое новое событие зависит только от предыдущего и не учитывает все остальные события. Такой алгоритм не помнит, что было раньше, а смотрит только на предыдущее состояние.
Случайным процессом называется множество или семейство случайных величин, значения которых индексируются временным параметром. Например, число студентов в аудитории, атмосферное давление или температура в этой аудитории как функции времени являются случайными процессами.
|
35
|
Приложения теории вероятностей в компьютерных науках.
|
Прогнозирование в различных сферах (Погода, Музыка…).
Data science; аналитика данных, машинное обучение.
|
36
|
Случайные числа, генераторы случайных чисел.
|
В основе метода Монте-Карло лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0; 1).
Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи, решаемой статистическим методом, может оказаться неверным. Поэтому проблема использования хорошего генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.

|
 Скачать 2.05 Mb.
Скачать 2.05 Mb.