лр. лр чужое. Представление заданной функции полиномом 8 11 Рис
 Скачать 326 Kb. Скачать 326 Kb.
|
|
Оглавление Введение 7 1.1 Представление заданной функции полиномом 8 11 Рис. 2. График разложения y=5x: 5 членов ряда, а1=0 11 12 Рис. 3. Ошибка разложения: 5 членов ряда, а1=0 12 14 Рис. 4. График разложения y=5x: 5 членов ряда, а2=2 14 15 Рис. 5. Ошибка разложения: 5 членов ряда, а2=2 15 Рис. 6. График разложения y=5x: 5 членов ряда, а3=3 17 18 Рис. 7. Ошибка разложения: 5 членов ряда, а3=3 18 Рис. 8. График разложения y=5x: 5 членов ряда, а4 = 4 20 Рис. 9. Ошибка разложения: 5 членов ряда, а4=4 21 1.2 Разработка рабочего алгоритма 22 Разработка вычислительного (арифметического) алгоритма вычисления заданной функции. 23 Любое решение вычислительной задачи численным методом сводится к разработке строго определенной последовательности арифметических операций. Назовем такую последовательность арифметическим алгоритмом. Таких арифметических алгоритмов для решения конкретной задачи могут быть разработано несколько. Для окончательной реализации необходимо выбрать оптимальный. Критериями оптимальности являются: наименьшее общее число арифметических операций, наименьшее число сложных операций типа умножения и деления переменных, желаемая точность вычислений. На этом этапе необходимо определить наибольшие и наименьшие значения входных, выходных и промежуточных переменных. Важным моментом является уточнение значений постоянных в выбранном алгоритме. 23 В подразделе 1.1. было обосновано применение приближенной формулы для вычисления заданной функции в следующем виде: 23 23 Диапазон измерений должен быть x, принадлежащий [0,0625; 8], а шаг 0.125. Рассмотрим три варианта расчета. 23 Вариант 1: исходная формула. Раскроем факториал. 23 23 Вариант 2: Преобразования по схеме Горнера 23 ))) 24 Вариант 3: преобразования по схеме Горнера в «дробь» 24 24 В таблице 1 представлены арифметические алгоритмы вычисления заданной функции тремя вариантами. 24 Вариант 1 24 Вариант 2 24 Вариант 3 24 y1 = x-4 24 y2 = 625*ln(5) 24 y3 = y2*y1 24 y4 = 625 + y3 24 y5 = ln(5)*ln(5) 24 y6 = 625*y5 24 y7 = y6/2 24 y8 = y1*y1 24 y9 = y7*y8 24 y10 = y4 + y9 24 y11 = y5*ln(5) 24 y12 = 625*y11 24 y13 = y12/6 24 y14 = y8*y1 24 y15 = y13*y14 24 y16 = y10 + y15 24 y17 = y11*ln(5) 24 y18 = 625*y17 25 y19 = y18/24 25 y20 = y14*y1 25 y21 = y19*y20 25 y22 = y16 + y21 25 y1 = x-4 24 y2 = ln(5)*y1 24 y3 = y2/4 24 y4 = 1 + y3 24 y5 = y2/3 24 y6 = 1 + y5 24 y7 = y6*y4 24 y8 = y2/2 24 y9 = 1+y8 24 y10 = y9*y7 24 y11 = 625*y2 24 y12 = y11*y10 24 y13 = 625 + y12 24 y1 = x-4 24 y2 = ln(5)*y1 24 y3 = 4+y2 24 y4 = y2*y3 24 y5 = 12+y4 24 y6 = y2*y5 24 y7 = 24+y6 24 y8 = y2*625 24 y9 = y8*y7 24 y10 = 15000+y9 24 y = y11 = y10/24 24 22 операций: 25 Сложений/вычитаний: 5 Умножений: 14 25 Делений на постоянную: 3 25 13 операций: 25 Сложений/вычитаний: 5 Умножений: 5 25 Делений на постоянную: 3 25 11 операций: 25 Сложений/вычитаний: 5 Умножений: 5 25 Делений на постоянную: 1 25 2. Конструкторская часть 26 2.1. Масштабирование рабочего полинома 26 Таблица 2. Результат масштабирования 30 2.2 Разработка ядра программы вычисления рабочего полинома 30 Таблица 3. Разработка ядра программы вычисления рабочего полинома 31 3.Экспериментальная часть 31 1.1.Результаты работы программы 31 Числовые характеристики ошибки вычисления при stx = 2-3. 33 Относительная приведенная погрешность, в % 33 395,1676% 33 Дисперсия 33 Математическое ожидание 33 26081,06 33 33 Рис. 10. Эталонный график функции 5x 34 34 Рис. 11. График разложения y=5x: 5 членов ряда, а4 = 4 34 34 Рис. 12. График, построенный по полученным значениям ассемблерной программы. 34 Рис. 13. График ошибки разложения: 5 членов ряда, а4=4 35 35 Рис. 14. График ошибки при вычислениях ассемблерной программы. 35 2. Заключение 36 Рассмотренная в данной работе теория масштабирования данных в ЦВМ с фиксированной запятой и практические примеры применения этой теории убеждают в высокой эффективности применения этого класса компьютеров при организации вычислительных процессов. Большим достоинством предложенной методики проектирования ассемблерных программ для вычислительных процессов является возможность разработки на её основе модулей системы автоматизированного проектирования (САПР) таких программ. 36 Методика служит хорошей основой при проектировании программ для многоядерных сигнальных процессоров и систем параллельной обработки информации на основе видеокарт. 36 Список использованной литературы 37 Введение Для того чтобы компьютер мог выполнить команды пользователя на аппаратном уровне, необходимо сгенерировать определенную последовательность действий с помощью машинного кода. Машинный код – это совокупность команд конкретной электронной вычислительной машины, которая интерпретируется процессором. Для удобства управления машинными кодами используются языки программирования низкого уровня. Язык ассемблера – это язык низкого уровня с командами, не всегда соответствующими командам машины, который позволяет обеспечить дополнительные возможности (макрокоманды). Ассемблер – это переводчик исходного текста программы, написанной на языке ассемблера, в программу на машинном коде. Современные системы управления сложными техническими объектами немыслимы без встраиваемых в эти системы вычислительных устройств. Особенностями таких вычислительных устройств являются работа в реальном масштабе времени и решение поставленных задач с заданной точностью. При этом их вычислительная нагрузка в основном определяется необходимостью выполнять большой объем арифметических операций. Реализация сложных вычислительных алгоритмов в системах управления многих реальных технических объектов с помощью микропроцессоров, имеющих команды плавающей арифметики, не всегда экономически и технически рациональна. Снять многие технические проблемы при разработке специализированного программного обеспечения разработчику помогут знание теории и практика программирования вычислительных алгоритмов на ассемблере для ЦВМ с фиксированной запятой. В данной работе представлена инженерная методика проектирования ассемблерных программ, реализующих вычислительные алгоритмы. 1. Исследовательская часть. 1.1 Представление заданной функции полиномом Исходные данные. Заданная функция y = 5x , диапазон изменения аргумента x 0,0625; 8 , шаг изменения аргумента stx = 2-3. Решение. Получим с помощью Excel значения заданной функции (таблица 1) и построим ее график (рисунок 1). Эти значения функции и ее график примем как эталонные. Таблица 1 Значения заданной функции
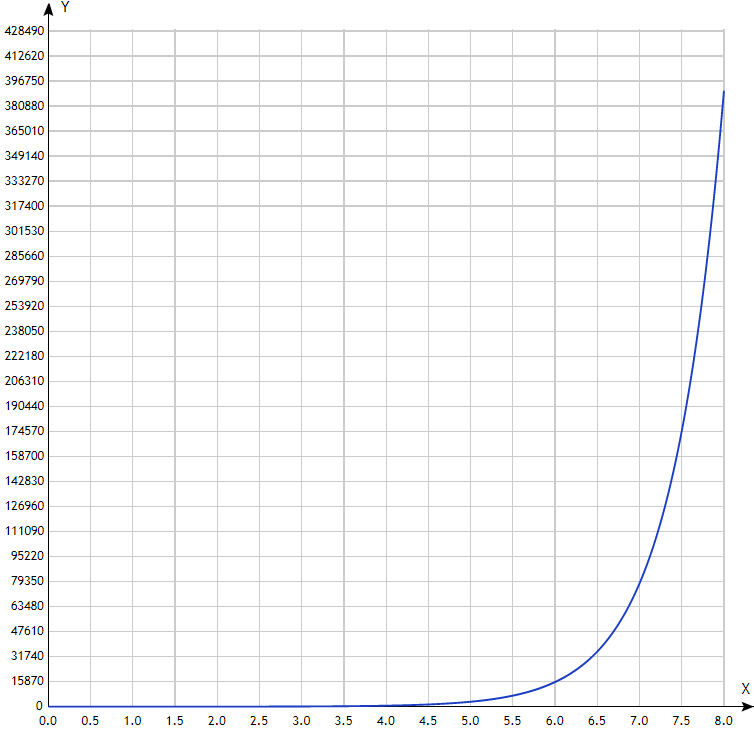 Рис.1. График эталонной функции Разложение заданной функции в ряд Тейлора в общем виде записывается следующим выражением: 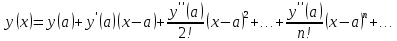 (1) (1)Здесь a точка разложения. Критериями выбора точки a являются: наименьшее число арифметических операций при реализации разложения; максимальная точность разложения заданной функции. Учитывая сказанное, выберем a1 = 0, a2 = 2, a3 = 3, a4 = 4 По условию имеем функцию y = 5x, поэтому будем рассматривать 5 членов ряда, так как с увеличением количества членов ряда уменьшается погрешность. Подставляя значения выбранных точек в уравнение (1) и произведя необходимые действия, получим искомые разложения: для а1 = 0 (ряд Маклорена): 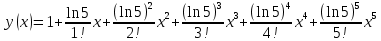 |
