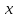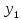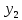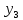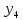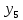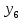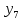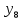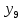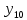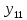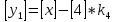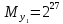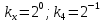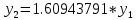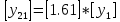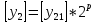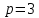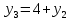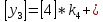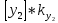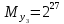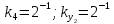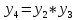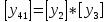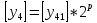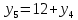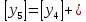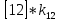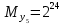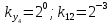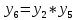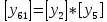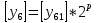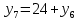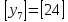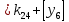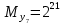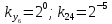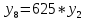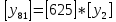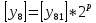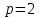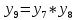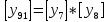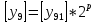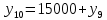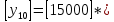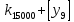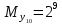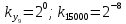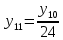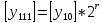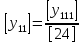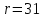лр. лр чужое. Представление заданной функции полиномом 8 11 Рис

• Название: Представление заданной функции полиномом 8 11 Рис
• Дата: 27.06.2022
• Размер: 326 Kb.
• Имя файла: лр чужое.docx
• Тип: Документы; #616520
• страница: 3 из 5

(6)

Разложение с пятью ненулевыми членами для a3 = 3: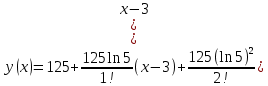

(7)
Результаты расчетов отражают следующие графики для a3 = 3 и пяти членах ряд Тейлора:

5 членов ряда, a = 3
X	Y	X	Y	X	Y
0,0625	1331,513	2,8125	92,44103	5,5625	4671,777
0,1875	1094,133	2,9375	113,038	5,6875	5343,862
0,3125	890,7594	3,0625	138,2279	5,8125	6090,231
0,4375	717,9044	3,1875	169,0285	5,9375	6916,407
0,5625	572,286	3,3125	206,6623	6,0625	7828,117
0,6875	450,827	3,4375	252,5568	6,1875	8831,294
0,8125	350,6545	3,5625	308,344	6,3125	9932,073
0,9375	269,1008	3,6875	375,8607	6,4375	11136,8
1,0625	203,7026	3,8125	457,1485	6,5625	12452,01
1,1875	152,2017	3,9375	554,4539	6,6875	13884,47
1,3125	112,5444	4,0625	670,2278	6,8125	15441,12
1,4375	82,88181	4,1875	807,1263	6,9375	17129,14
1,5625	61,56989	4,3125	968,01	7,0625	18955,87
1,6875	47,16931	4,4375	1155,944	7,1875	20928,91
1,8125	38,44548	4,5625	1374,199	7,3125	23056,01
1,9375	34,3686	4,6875	1626,25	7,4375	25345,16
2,0625	34,11363	4,8125	1915,776	7,5625	27804,54
2,1875	37,06027	4,9375	2246,662	7,6875	30442,54
2,3125	42,79302	5,0625	2622,997	7,8125	33267,76
2,4375	51,10108	5,1875	3049,074	7,9375	36289
2,5625	61,97848	5,3125	3529,394	8,0625	39515,25
2,6875	75,62396	5,4375	4068,659

синий – функция эталона

красный – функция разложения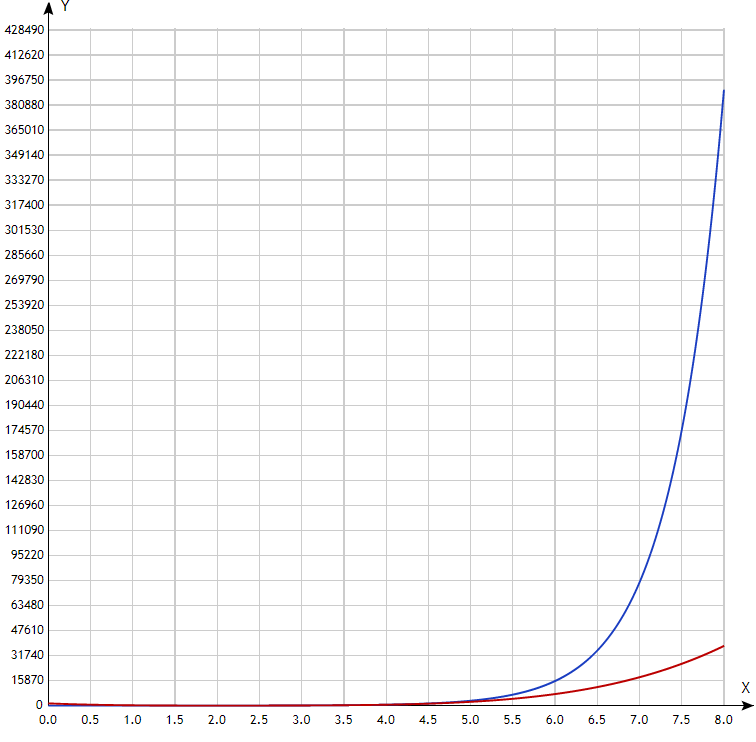


Рис. 6. График разложения y=5^x: 5 членов ряда, а3=3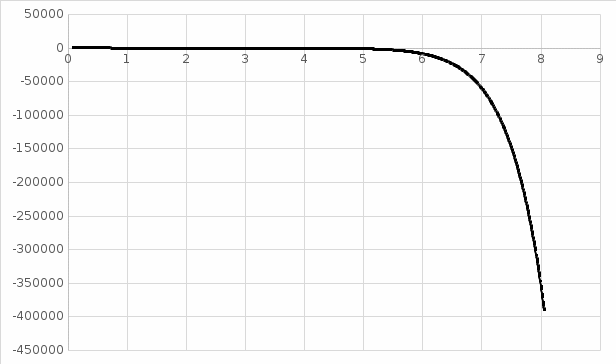



Рис. 7. Ошибка разложения: 5 членов ряда, а3=3
Подставляя значения выбранных точек в уравнение (1) и произведя необходимые действия, получим искомые разложения:

для а4 = 4: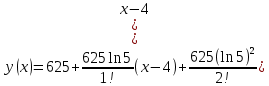

(8)

Разложение с пятью ненулевыми членами для a4 = 4: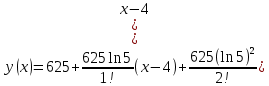

(9)
Результаты расчетов отражают следующие графики для a4 = 4 и пяти членах ряд Тейлора:

5 членов ряда, a = 4
X	Y	X	Y	X	Y
0,0625	24703,82	2,8125	192,2274	5,5625	6870,996
0,1875	21406,18	2,9375	171,843	5,6875	8131,249
0,3125	18454,91	3,0625	170,5681	5,8125	9578,879
0,4375	15824,37	3,1875	185,3014	5,9375	11233,31
0,5625	13489,98	3,3125	213,9651	6,0625	13114,98
0,6875	11428,14	3,4375	255,5054	6,1875	15245,37
0,8125	9616,307	3,5625	309,8924	6,3125	17646,97
0,9375	8032,951	3,6875	378,1198	6,4375	20343,29
1,0625	6657,565	3,8125	462,2052	6,5625	23358,89
1,1875	5470,667	3,9375	565,19	6,6875	26719,31
1,3125	4453,797	4,0625	691,1393	6,8125	30451,16
1,4375	3589,522	4,1875	845,1423	6,9375	34582,04
1,5625	2861,43	4,3125	1033,312	7,0625	39140,59
1,6875	2254,135	4,4375	1262,784	7,1875	44156,47
1,8125	1753,273	4,5625	1541,72	7,3125	49660,37
1,9375	1345,504	4,6875	1879,303	7,4375	55683,99
2,0625	1018,513	4,8125	2285,743	7,5625	62260,06
2,1875	761,0086	4,9375	2772,269	7,6875	69422,35
2,3125	562,722	5,0625	3351,139	7,8125	77205,62
2,4375	414,4091	5,1875	4035,632	7,9375	85645,69
2,5625	307,8495	5,3125	4840,05	8,0625	94779,37
2,6875	235,8465	5,4375	5779,721

синий – функция эталона

красный – функция разложения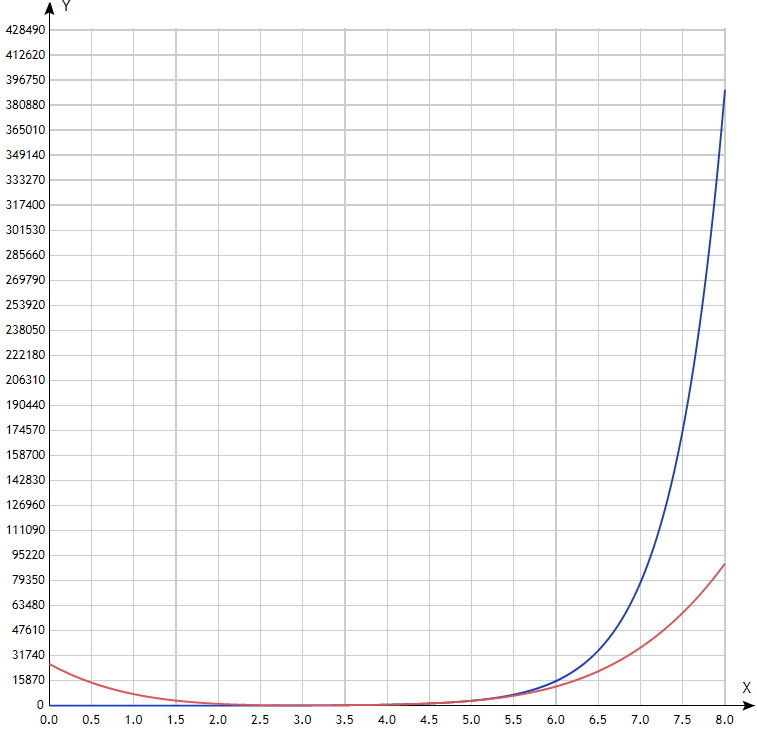


Рис. 8. График разложения y=5^x: 5 членов ряда, а4 = 4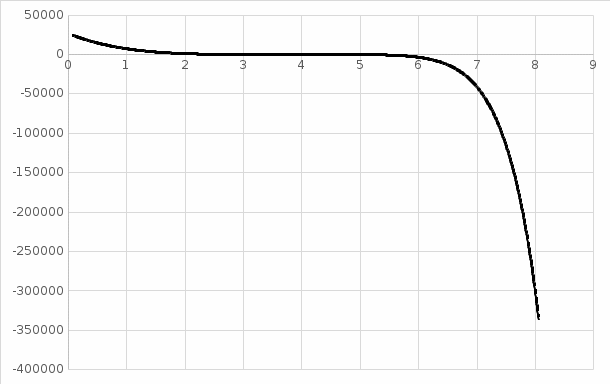



Рис. 9. Ошибка разложения: 5 членов ряда, а4=4
Проанализировав графики ошибок разложения рядов, можно сделать вывод, что наиболее точным рядом разложения является (9) при а4 = 4.
В таблице ниже приведены статистические числовые характеристики ошибок разложения функции y5^x в ряд Тейлора в точке разложения а4=4.

	Число членов ряда Тейлора(значение а)
	5(0)	5(2)	5(3)	5(4)
Наибольшая абсолютная погрешность	-0,000292392	39	1330	24702
Наибольшая приведенная относительная погрешность	6519%	3584%	5946%	5108%
Математическое ожидание погрешности	35547,3	33811,7	30179,7	21342,5
Дисперсия погрешности	7381872301	6843593715	5912043226	4273108276

Проанализируем полученные результаты. Для поставленной задачи, когда необходимо вычислять y=5^x целесообразнее всего применять ряд Тейлора при а = 4.

Анализируя тенденцию повышения точности, приходим к выводу – точность растет при увеличении количества членов ряда, и с каждым членом точность вырастает в 1,5 – 2 раза. Следовательно, оптимальным и достаточно точным решением будет ряд Тейлора как минимум с 16 членами ряда, и как максимум с 25 членами ряда. Учитывая нестабильность, приходим к выводу: разработанный алгоритм должен иметь возможность самостоятельно добавлять члены к ряду, для получения достаточной точности. А значит, разработку алгоритма можно продолжить, используя уравнение (9).

1.2 Разработка рабочего алгоритма
Исходные данные.

Заданная функция y = 5^x , диапазон изменения аргумента x 0,0625; 8 , шаг изменения аргумента stx = 2^-3.
Разработка вычислительного (арифметического) алгоритма вычисления заданной функции.

Любое решение вычислительной задачи численным методом сводится к разработке строго определенной последовательности арифметических операций. Назовем такую последовательность арифметическим алгоритмом. Таких арифметических алгоритмов для решения конкретной задачи могут быть разработано несколько. Для окончательной реализации необходимо выбрать оптимальный. Критериями оптимальности являются: наименьшее общее число арифметических операций, наименьшее число сложных операций типа умножения и деления переменных, желаемая точность вычислений. На этом этапе необходимо определить наибольшие и наименьшие значения входных, выходных и промежуточных переменных. Важным моментом является уточнение значений постоянных в выбранном алгоритме.

В подразделе 1.1. было обосновано применение приближенной формулы для вычисления заданной функции в следующем виде: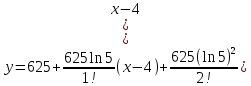



Диапазон измерений должен быть x, принадлежащий [0,0625; 8], а шаг 0.125. Рассмотрим три варианта расчета.

Вариант 1: исходная формула. Раскроем факториал.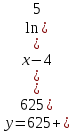



Вариант 2: Преобразования по схеме Горнера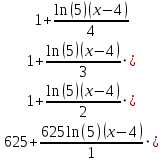

)))


Вариант 3: преобразования по схеме Горнера в «дробь»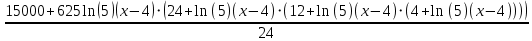


В таблице 1 представлены арифметические алгоритмы вычисления заданной функции тремя вариантами.

Вариант 1	Вариант 2	Вариант 3
y1 = x-4 y2 = 625*ln(5) y3 = y2*y1 y4 = 625 + y3 y5 = ln(5)*ln(5) y6 = 625*y5 y7 = y6/2 y8 = y1*y1 y9 = y7*y8 y10 = y4 + y9 y11 = y5*ln(5) y12 = 625*y11 y13 = y12/6 y14 = y8*y1 y15 = y13*y14 y16 = y10 + y15 y17 = y11*ln(5) y18 = 625*y17 y19 = y18/24 y20 = y14*y1 y21 = y19*y20 y22 = y16 + y21	y1 = x-4 y2 = ln(5)*y1 y3 = y2/4 y4 = 1 + y3 y5 = y2/3 y6 = 1 + y5 y7 = y6*y4 y8 = y2/2 y9 = 1+y8 y10 = y9*y7 y11 = 625*y2 y12 = y11*y10 y13 = 625 + y12	y1 = x-4 y2 = ln(5)*y1 y3 = 4+y2 y4 = y2*y3 y5 = 12+y4 y6 = y2*y5 y7 = 24+y6 y8 = y2*625 y9 = y8*y7 y10 = 15000+y9 y = y11 = y10/24
22 операций: Сложений/вычитаний: 5 Умножений: 14 Делений на постоянную: 3	13 операций: Сложений/вычитаний: 5 Умножений: 5 Делений на постоянную: 3	11 операций: Сложений/вычитаний: 5 Умножений: 5 Делений на постоянную: 1

Как видно из таблицы, наименьшее число всех операций и наименьшее число сложных операций типа умножение/деление имеет алгоритм третьего варианта. Этот вариант примем для дальнейшей работы.

2. Конструкторская часть

2.1. Масштабирование рабочего полинома

Переменная	Максимальное значение
	8
	4.0625
	6.538341519
	10.53834152
	68.9032759
	80.9032759
	528.9732479
	552.9732479
	4086.46345
	2,259,704.966
	2,274,704.966
	94,779.37358

Разработка проекта машинного алгоритма:

Масштабирование начинаем с первой операции рабочего алгоритма.

Операция 1.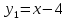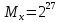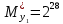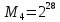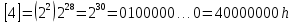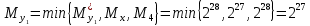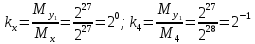













Операция 2.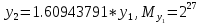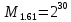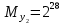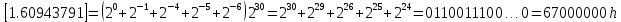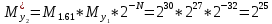









Определим запас точности: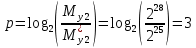

Операция 3.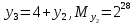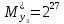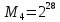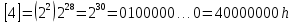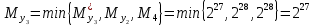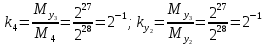











Операция 4.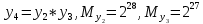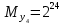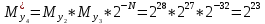





Определим запас точности: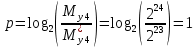

Операция 5.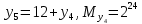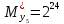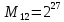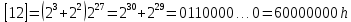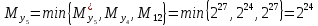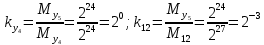











Операция 6.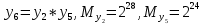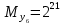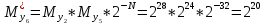





Определим запас точности: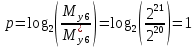

Операция 7.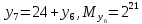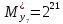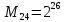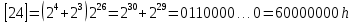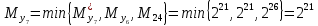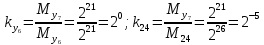











Операция 8.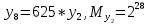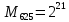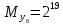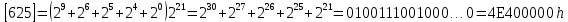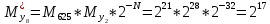









Определим запас точности: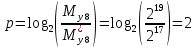

Операция 9.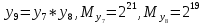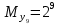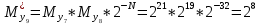





Определим запас точности: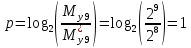

Операция 10.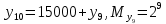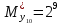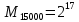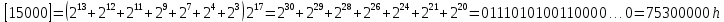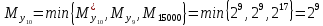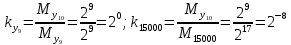











Операция 11.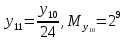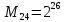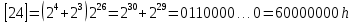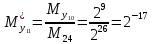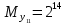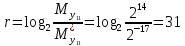










Сведем полученные результаты в таблицу 2.

Арифметический алгоритм	Машинный алгоритм	Масштабные соотношения

Таблица 2. Результат масштабирования