Физика 1-15. Преобразования Галилея

Название	Преобразования Галилея
Анкор	Физика 1-15.docx
Дата	28.12.2017
Размер	230.96 Kb.
Формат файла
Имя файла	Физика 1-15.docx
Тип	Документы #13323
страница	4 из 4

1 2 3 4

Билет 9

ако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.

ассмотрим второй закон Ньютона

$\frac{d\vec {p}}{dt}=\vec {f}.$

Перепишем его для системы из N частиц: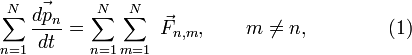

$\sum_{n=1}^{n} \frac{\vec{dp_n}}{dt}=\sum_{n=1}^{n}\sum_{m=1}^{n}\ \vec{f}_{n,m}, \qquad m\ne n, \qquad\qquad (1)$

где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида 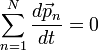$\vec {f}_{a,b}$ и $\vec {f}_{b,a}$ будут равны по абсолютному значению и противоположны по направлению, то есть $\vec{f}_{a,b} = -\vec{f}_{b,a}.$ Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

$\sum_{n=1}^{n} \frac{d\vec{p}_n}{dt}=0$

или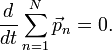

$\!\qquad \frac {d}{dt}\sum_{n=1}^{n}\vec{p}_n=0.$

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит: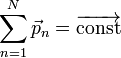

$\sum_{n=1}^{n}\vec{p}_n=\overrightarrow {\mathrm{const}} \qquad\!$ (постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.

Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы.

Также стоит подчеркнуть, что изменение импульса $d\vec {p}$ зависит не только от действующей на тело силы, но и от продолжительности её действия.

Билет 10

Систе́ма це́нтра масс (систе́ма це́нтра ине́рции) — невращающаяся система отсчёта, связанная с центром масс механической системы. Обычно сокращается как с. ц. м. или с. ц. и. Суммарный импульс системы в с.ц.м. равен нулю. Для замкнутой системы её система центра масс инерциальна, тогда как незамкнутая система в общем случае может обладать неинерциальной системой центра масс. Суммарная кинетическая энергия механической системы в с.ц.м. минимальна среди всех систем отсчёта; в любой другой невращающейся (не обязательно инерциальной) системе отсчёта кинетическая энергия равна кинетической энергии в с.ц.м. плюс кинетическая энергия движения механической системы как целого (MV²/2, где М — полная масса механической системы, V — относительная скорость движения систем отсчёта).

При рассмотрении задач рассеяния частиц термин «система центра масс» употребляется как антоним термина «лабораторная система отсчёта».

Если экспериментальные исследования проводятся в лабораторной системе, то есть в системе, связанной с наблюдателем (неподвижным относительно частицы-мишени), то теоретическое рассмотрение задач рассеяния удобно проводить в движущейся относительно мишени системе центра масс. При переходе от лабораторной системы в систему центра масс меняются определения углов рассеяния частиц, так что для сравнения теории с экспериментом необходимо проводить перерасчёт полученных сечений рассеяния.

Например, при изучении столкновения двух одинаковых частиц, одна из частиц (мишень) до столкновения остается неподвижной, вторая налетает с некоторой конечной скоростью. При упругом лобовом столкновении вторая частица останавливается, передавая всю свою кинетическую энергию и импульс первой частице. Такая картина наблюдается в лабораторной системе отсчета. С точки зрения системы центра масс, частицы движутся навстречу друг другу с одинаковыми скоростями и после столкновения разлетаются в обе стороны с теми же (с точностью до знака) скоростями.

В нерелятивистском пределе координаты центра масс системы из n частиц, имеющих массы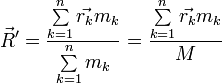

и (в некоторой системе отсчёта К) радиус-векторы $\vec{r_k}$ :

$\vec{r}^{\prime}=\frac{\sum\limits_{k=1}^{n}{\vec{r_k}m_{k}}}{\sum\limits_{k=1}^{n}{m_{k}}}=\frac{\sum\limits_{k=1}^{n}{\vec{r_k}m_{k}}}{m}$

(М — масса всей системы тел). Продифференцировав по времени, получим скорость движения центра масс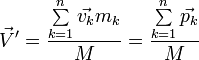

$\vec{v}^{\prime}=\frac{\sum\limits_{k=1}^{n}{\vec{v_k}m_k}}{m}=\frac{\sum\limits_{k=1}^{n}{\vec{p_k}}}{m}$

( $\vec{p_k}$ — импульсы частиц), которую можно использовать для перехода от данной системы отсчёта К к системе центра масс, вычисляя скорости и радиус-векторы частиц в ней по формулам:

$\vec{r_k}^{\prime} = \vec{r_k} - \vec{r}^{\prime},$

$\vec{v_k}^{\prime} = \vec{v_k} - \vec{v}^{\prime}.$

В релятивистском случае центр масс не является лоренц-инвариантом, однако система центра масс определяется и играет важную роль в релятивистской кинематике. Систему центра масс в релятивистском случае следует определять как систему отсчёта, в которой сумма импульсов всех тел системы равна нулю.

Билет 11

Работа силы. Мощность

Работа силы. МощностьРабота. По определению работой постоянной силы F, совершаемой при перемещении тела на величину s, называется величина

(14.1)

где a - угол между векторами F и s. Если воспользоваться понятием скалярного произведения двух векторов, то выражение для работы можно записать в виде:

Работа измеряется в джоулях (Дж): [A] = Дж = Н·м.

Следует обратить внимание на то, что механическая работа совершается только тогда, когда тело движется (просто прикладывая силу к тяжелому телу и пытаясь сдвинуть его с места, вы не совершаете механической работы, хотя и тратите мускульную энергию). Во-вторых, величина работы зависит от угла между векторами F и s.

Если на тело действуют несколько сил, то полная работа, совершенная этими силами, равна сумме работ, совершенных каждой силой в отдельности. Это следует из принципа суперпозиции сил.

Мощность. Пусть сила F, действуя в течение промежутка времени Dt, совершает работу DA. Средняя мощность N определяется как отношение величины работы к промежутку времени, за который она была совершена: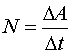

n = a / t

(14.2)

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона: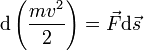

$m \vec a = \vec f$

$\vec{f}$ — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы ${\rm d} \vec s = \vec v {\rm d}t$ . Учитывая, что $\vec a = \frac{{\rm d}\vec{v}}{{\rm d}t}$ , Получим:

${\rm d} \left( {{m v^2} \over {2}} \right) = \vec f {\rm d} \vec s$

Если система замкнута, то есть 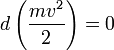$\vec f = 0$ , то $d \left( {{m v^2} \over {2}} \right) = 0$ , а величина

$t = {{m v^2} \over 2}$

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

$t = \frac{m v^2}{2}+\frac{\mathcal{i} \vec \omega^2}{2}$

где:

$\ m$ — масса тела

$\ v$ — скорость центра масс тела

$\mathcal{i}$ — момент инерции тела

$\vec \omega$ — угловая скорость тела.

Билет 12

В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил)^[1]. Отсюда следует определение: консервативные силы — такие силы, работа которых по любойзамкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

$\nabla \times \vec{f} = 0$ — ротор консервативных сил равен 0;

$\oint\limits_c {\vec{f} d\vec{l}} = 0$ — работа консервативных сил по произвольному замкнутому контуру равна 0;

$\vec{f} = \nabla u$ — консервативная сила является градиентом некой скалярной функции

, называемой силовой. Эта функция равна потенциальной энергии

взятой с обратным знаком. Соответственно, $\vec{f}$ и

связаны соотношением

$\vec{f} = -\nabla e_p.$

Таким образом, потенциальная сила всегда направлена против направления возрастания потенциальной энергии.

В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.

В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия).

Потенциальная энергия $u(\vec r)$ — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела

отенциальная энергия $\ e_p$ в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

$\ e_p=mgh$

где $\ m$ — масса тела, $\ g$ — ускорение свободного падения, $\ h$ — высота положения центра масс тела над произвольно выбранным нулевым уровнем

Билет 13

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципомсохранения энергии.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимостью законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Говорят, что возможен переход энергии одного типа в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Ввиду условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.

Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а вэлектродинамике — теорема Пойнтинга.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Фундаментальный смысл закона сохранения энергии раскрывается теоремой Нётер. Согласно этой теореме каждый закон сохранения однозначно соответствует той или иной симметрииуравнений, описывающих физическую систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.

Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма^[1]. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид: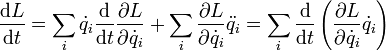

$\frac{{\rm d}l}{{\rm d}t} = \sum_i\frac{\partial l}{\partial q_i}\dot q_i + \sum_i\frac{\partial l}{\partial \dot q_i}\ddot q_i$

Здесь $l(q_i, \dot q_i)$ — функция Лагранжа, $q_i, \dot q_i, \ddot q_i$ — обобщённые координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные $\frac{\partial l}{\partial q_i}$ на выражение $\frac{\rm d}{{\rm d}t}\frac{\partial l}{\partial \dot q_i}$ :

$\frac{{\rm d}l}{{\rm d}t} = \sum_i\dot q_i\frac{\rm d}{{\rm d}t}\frac{\partial l}{\partial \dot q_i} + \sum_i\frac{\partial l}{\partial \dot q_i}\ddot q_i = \sum_i\frac{\rm d}{{\rm d}t}\left(\frac{\partial l}{\partial \dot q_i}\dot q_i\right)$

Перепишем последнее выражение в виде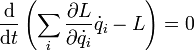

$\frac{\rm d}{{\rm d}t}\left(\sum_i\frac{\partial l}{\partial \dot q_i}\dot q_i - l\right) = 0$

Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).

Билет 14

Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называетсякоэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.

В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

$f_{\text{tp}}=k \cdot n\!$ , где

$k\!$ — коэффициент трения скольжения,

$n\!$ — сила нормальной реакции опоры.

Билет 15

В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.

1 2 3 4