Физика 1-15. Преобразования Галилея
 Скачать 230.96 Kb.
|
Криволинейное движениеКриволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времениt определяется по формулам      Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением  где r – радиус окружности.Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости. При криволинейном движении ускорение можно представить как сумму нормальной  и тангенциальной  составляющих: , - нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению: v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке. - тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.Полное ускорение, с которым движется материальная точка, равно: 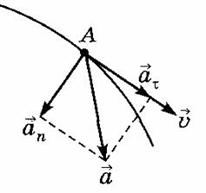 . Кроме центростремительного ускорения, важнейшими характе ристиками равномерного движения по окружности являются период и частота обращения. Период обращения— это время, за которое тело совершается один оборот. Обозначается период буквой Т (с) и определяется по формуле:  где t — время обращения, п — число оборотов, совершенных за это время. Частота обращения— это величина, численно равная числу оборотов, совершенных за единицу времени. Обозначается частота греческой буквой  (ню) и находится по формуле: Измеряется частота в 1/с. Период и частота — величины взаимно обратные:  Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив ско рость v на время одного оборота: l = vT. С другой стороны, этот путь равен длине окружности 2πr. Поэтому vT = 2πr,   где w (с-1) - угловая скорость. При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения. Угловая скорость (w) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:  .Связь между линейной и угловой скоростями: v= wr. Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе. БИЛЕТ 5 Первый закон Ньютона Основная статья: Инерция Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тел Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). |