Физика 1-15. Преобразования Галилея

• Название: Преобразования Галилея
• Анкор: Физика 1-15.docx
• Дата: 28.12.2017
• Размер: 230.96 Kb.
• Имя файла: Физика 1-15.docx
• Тип: Документы; #13323
• страница: 3 из 4

[править]Современная формулировка

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:



где  — ускорение материальной точки;
 — сила, приложенная к материальной точке;
 — масса материальной точки.

Или в более известном виде:



В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:

В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.

где  — импульс точки,



где  — скорость точки;

 — время;
 — производная импульса по времени.

Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:



или



Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.

Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.

Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.

[править]Современная формулировка

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

Ма́сса (от греч. μάζα) — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя).

В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «массы» можно трактовать несколькими способами:

• 
  Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.
  
• 
  Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.
  
• 
  Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
  

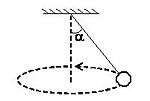
Гравитационная и инертная массы равны друг другу (с высокой точностью — порядка 10⁻¹³ — экспериментально^[1][2], а в большинстве физических теорий, в том числе всех, подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт не о «новой физике», просто говорят о массе, не уточняя, какую из них имеют в виду.

В классической механике масса системы тел равна сумме масс составляющих её тел. В релятивистской механике масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс компонентов, а включает в себя энергию связи, а также энергию движения частиц друг относительно друга^[3].

И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

.

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нёмдеформаций.^[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).^[2].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.^[3][4][5][6]

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.^[3] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.^[7]

Размерность силы — LMT⁻², единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

БИЛЕТ 7

Влияние гравитационного поля на движение частиц в ньютоновской механике хорошо изучено. Уравнение движения частицы представляет собой уравнение в левой части которого стоит ускорение пробной частицы умноженное на массу частицы (в данном случае это инертная масса), в правой части уравнения стоит гравитационная сила. Гравитационная сила, в свою очередь, представляет из себя произведение массы пробной частицы (в данном случае - гравитационной массы) на ускорение со стороны тяготеющего тела: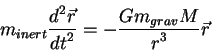 

 

Поскольку инертная масса тела равна его гравитационной массе (это формулировка принципа эквивалентности, многократно проверенного экспериментально), то движение пробной частицы не зависит от массы этой частицы - перо птицы и кирпич падают в гравитационном поле с одинаковым ускорением (конечно, если пренебречь сопротивлением воздуха).

В общей теории относительности роль гравитационной силы играет кривизна пространства - времени. Движение в гравитационном поле - это движение в искривленном пространстве, отклонение от движения по прямой линии - это отклонение в движении возникающее в искривленном пространстве времени.

Вспомним вначале уравнения движения в специальной теории относительности.

БИЛЕТ 8

Сила упругости

Вид деформации	Признаки
Растяжения	увеличивается расстояние между молекулярными слоями.
Сжатия	уменьшается расстояние между молекулярными слоями.
Кручения	поворот одних молекулярных слоев относительно других.
Изгиба	одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых.
Сдвига	одни слои молекул сдвигаются относительно других.
Упругая	после прекращения воздействия тело полностью восстанавливает первоначальную форму и размеры.
Пластичная	после прекращения воздействия тело не восстанавливает первоначальную форму или размеры.

 Δl=|l−l0| ,

где Δl – абсолютное удлинение (м); l и l₀ – конечная и начальная длина тела (м).

• 
  Если тело растягивают, то l > l₀ и Δl = l – l₀;
  
• 
  если тело сжимают, то l < l₀ и Δl = –(l – l₀) = l₀ – l.
  

 ε=Δll0 или  ε=Δll0⋅100 ,

где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l₀ –начальная длина тела (м).

 σ=FuprS ,

где σ – механическое напряжение в деформированном теле (Па); F_upr – модуль силы упругости, возникающей в теле при деформации (Н); S – площадь поперечного сечения тела (м²).

 σ=Eε ,

где σ – механическое напряжение (Па); Е – модуль Юнга (модуль упругости), табличная величина (Па); ε – относительное удлинение (%).

 Fupr=kΔl ,

где F_upr – модуль силы упругости, возникающей в теле при деформации (Н); k – коэффициент жесткости (жесткость) тела (Н/м); Δl – абсолютное удлинение тела (м).

 σpr=FmaxS ,

где σ_pr – предел прочности (Па); F_max – максимальная сила, которую может выдержать тело, не разрушаясь (Н); S – площадь поперечного сечения тела (м²).

• 
  При одномерных (линейных) деформациях растяжения или сжатия силы упругости направлены вдоль линии действия внешней (деформирующей) силы, т.е. вдоль осей продольно деформируемых нитей, витых пружин, стержней и т.п., или перпендикулярно к поверхностям соприкасающихся тел.
  

• 
  Функция вида у = k·х – линейная, график такой функции прямая линия, проходящая через начало координат. Уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения F_upr = k·Δl. Это так же линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.
  

• 
  Если ось 0Х направить вдоль тела в сторону его растяжения, начало отсчета выбрать в точке, совпадающей с концом недеформированного тела (рис. 1), то закон Гука можно записать так:
  

 (Fupr)x=−k⋅x ,

где (F_upr)_x – проекция сила упругости на ось 0Х (Н); х – координата конца тела.

• 
  Знак «–» указывает, что сила упругости всегда противоположна по направлению абсолютному удлинению.
  

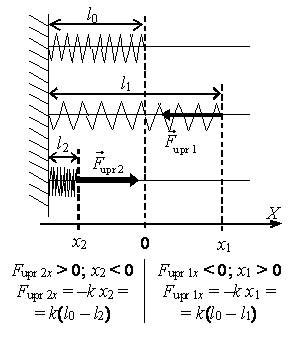Рис. 1

Всемирное тяготение

 F=G⋅m1m2r2 ,

где F – сила всемирного тяготения (Н); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; m₁ и m₂ – массы взаимодействующих тел (кг); r – расстояние между телами (м).

• 
  Математические правила
  

х·10^a · y·10^b = x·y·10^a+b; х·10^a / (y·10^b) = x/y·10^a-b ; (x·10^a)ⁿ = xⁿ·10^an.

Например: 1,2·10^-11·(5·10¹⁰)² / (4·10¹⁵) = 1,2·(5)²/4 ·10^{-11 + 10·2 – 15} = 7,5·10^-6.

 Ft=mgpl ,

где F_t – сила тяжести (Н); g_pl – ускорение свободного падения планеты, табличная величина (м/с²); m – масса тела (кг).

• 
  g ≈ 9,81 м/с² – ускорение свободного падения у поверхности Земли.
  

 Ft=G⋅Mplmr2 ,

где F_t – сила тяжести (сила притяжения) на планете (Н); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); m – масса тела (кг); r = R_pl + h – расстояние от центра планеты до тела (м); R_pl – радиус планеты, табличная величина (м); h – высота тела над поверхностью планеты (м) (рис. 2).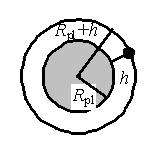



Рис. 2

 gpl=G⋅Mplr2 ,

где g_pl – ускорение свободного падения планеты, табличная величина (м/с²); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); r = R_pl + h – расстояние от центра планеты до тела (м); R_pl – радиус планеты, табличная величина (м); h – высота тела над поверхностью планеты (м) (рис. 2).

• 
  Вес Р – это сила, с которой тело, вследствие земного притяжения действует на опору или подвес, неподвижные относительно него.
  

Примеры направления силы Р показаны на рис. 3 а-г.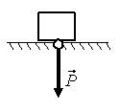

а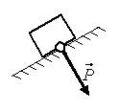 

б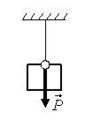 

в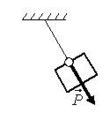 

г

Рис. 3

 Py=m⋅(gy−ay) ,

где Р_y – проекция веса тела на ось 0Y (Н); m – масса тела (кг); a_y – проекция ускорения тела на ось 0Y (м/с²); g_y – проекция ускорение свободного падения на ось 0Y (м/с²).

• 
  Если направить ось 0Y вниз, то вес тела будет равен:
  

а) P = m·(g – a) (рис. 4 а),

б) P = m·(g + a) (рис. 4 б),

в) –P = m·(g – a) (рис. 4 в), P = m·(a – g).

• 
  Если направить ось 0Y вверх, то вес тела будет равен:
  

г) P = m·(a – g) (рис. 4 г).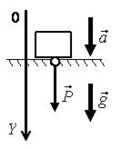

а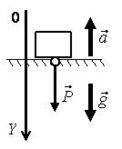

б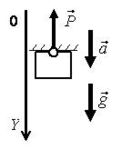

в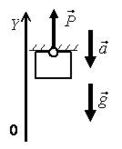 

г

Рис. 4

• 
  При прямолинейном движении:
  

– направления ускорения и скорости совпадают если значение скорости увеличивается;

– ускорение и скорость направлены в противоположные стороны, если значение скорости уменьшается.

• 
  При движении по окружности центростремительное ускорение направлено к центру окружности и равно  ac=υ2R .
  

 υ=G⋅Mplr−−−−−−√ ,

где υ – скорость ИС (м/с), G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); r = R_pl + h – расстояние от центра планеты до ИС (м); R_pl – радиус планеты, табличная величина (м); h – высота ИС над поверхностью планеты (м) (рис. 2).

• 
  Первая космическая скорость для данной планеты – это скорость, которую нужно сообщить спутнику, чтобы он двигался по круговой орбите вблизи поверхности планеты.
  

Сила трения

F_tr = F_{tr p} = F, если F ≤ F_{tr sk};

F_tr = F_{tr sk}, если F > F_{tr sk} ,

где F_tr – сила трения (Н); F_{tr p} – сила трения покоя (Н); F – сила, действующая на тело (рис. 5) (Н), F_{tr sk} – сила трения скольжения (Н).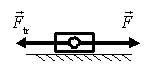



Рис. 5

 Ftrsk=μN ,

где F_{tr sk} – сила трения скольжения (Н); μ – коэффициент трения скольжения, табличная величина; N = P = F_davl – сила реакции опоры (Н); Р – вес тела (Н); F_davl – сила нормального давления (Н).

• 
  Уравнение второго закона Ньютона в векторной форме имеет вид  ma⃗ =F⃗ 1+F⃗ 2+F⃗ 3+…
  
• 
  Проекция вектора
  

– положительна, если составляющая вектора на данную ось направлена вдоль этой оси;

– отрицательна – если против оси;

– равна нулю – если вектор перпендикулярен оси.

• 
  При изображении сил, не забывайте, что равнодействующая сил должна быть направлена в сторону ускорения.
  

Движение под действием нескольких сил

• 
  Задачи, в которых на тело действуют несколько сил, решайте, придерживаясь следующего плана решения задач:
  
  1. 
     Сделайте чертеж. Укажите все действующие на тело силы, укажите направления скорости и ускорения. Изобразите оси координат.
     
  2. 
     Запишите второй закон Ньютона в векторном виде и в проекциях на оси координат:
     

 ma⃗ =F⃗ 1+F⃗ 2+F⃗ 3+… ,

OX

 max=F1x+F2x+F3x+…

,

OY

 may=F1y+F2y+F3y+…

Определите значения проекций всех величин.

1. 
   Решите полученные уравнения. При необходимости, исходя из физической природы, выразите силы через величины, от которых они зависят.
   

• 
  Если тело материальная точка, то его можно изобразить в виде прямоугольника или окружности, а все силы – выходящими из его центра;
  
• 
  если тело нельзя представить в виде материальной точки, то изображайте его, сохраняя форму, а силы изображайте с учетом точек их приложения.
  
• 
  При решении задач на движение тел под действием силы трения, часто необходимо использовать кинематические формулы.
  
• 
  При прямолинейном движении ускорение при торможении направлено против скорости;
  
• 
  при остановке конечная скорость равна нулю.
  
• 
  При равномерном движении по окружности тело движется с центростремительным ускорением, направленным к центру окружности и равным  ac=υ2R=ω2R .
  
• 
  Если в условии задачи говорится о системе материальных тел, то необходимо записывать уравнение второго закона Ньютона для каждого тела системы в отдельности.
  
• 
  Можно выбирать разные системы координат для разных тел.
  
• 
  Систему, изображенную на рис. 6 а, называют коническим маятником; на рис. 6 б – математическим маятником
  

аб

Рис. 6

• 
  Скорость конического маятника не меняется по величине, поэтому ускорение груза равно центростремительному ускорению, направленному к центру окружности.
  
• 
  Скорость математического маятника изменяется по величине, поэтому ускорение груза  a=a2c+a2τ−−−−−−√ , где а_c – центростремительное ускорение, направленное к центру окружности (вдоль подвеса); а_τ – тангенциальное ускорение, направленное также как и скорость (по касательной), если скорость увеличивается, и в противоположную сторону, если скорость уменьшается.
  
• 
  Если тело находится в системе, которая движется с ускорением, то можно применять несколько способ решения задач:
  

1 способ. Второй закон Ньютона записать в следующем виде

 ma⃗ t=F⃗ 1+F⃗ 2+…

, где  a⃗ t=a⃗ c+a⃗ t/c – ускорение тела относительно неподвижной системы (Земли),  a⃗ c – ускорение системы, в которой находится тело,  a⃗ t/c – ускорение тела относительно движущейся системы.

2 способ. Перейти в НИСО, тогда второй закон Ньютона будет иметь вид  ma⃗ t/c=F⃗ in+F⃗ 1+F⃗ 2+… , где  a⃗ t/c – ускорение тела относительно движущейся системы,  F⃗ in – сила инерции, которая направлена против ускорения системы а_c, а по величине равна F_in = m∙а_c,  a⃗ c – ускорение системы.