Задач. Задачи по статистике решённые. Пример задания 1
 Скачать 1.07 Mb.
|
|
По наименьшему расстоянию формируем два кластера 1,2,3 и 4,5,6.Таким образом, процесс кластерного анализа закончен. Выделено два кластера. Дендрограмма результатов кластерного анализа изображена на рис. 5.5.1. 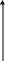  14 Расстояние  13,60 12 . . . . . . . . .     4 2  1 2 3 4 5 6 Номера объектов Рис. 5.5.1 Дендрограмма, представленная на рис 5.5.1, отличается от дендрограммы, представленной на рис. 5.1.5. Все остальные результаты примера 5.1 и примера 5.5 одинаковы. Повторим их с изменением номеров таблиц. Представим результаты кластерного анализа в виде совокупности двух матриц: расстояний между объектами (таблица 5.5.5) и символов Кронекера (таблица 5.5.6). Таблица 5.5.5
Таблица 5.5.6
Подсчитаем сумму расстояний между объектами:  0+2,83+3,16+10,19+12,17+13,60+0+ 0+ 3,16+ 8,94+10,77+12,53+ 0+ 0+ 0+ 7,07+ 9,06+10,44+ 0+ 0+ 0+ 0+ 2+ 3,61+ 0+ 0+ 0+ 0+ 0+ 2,24 =111,77. Среднее расстояние = 111,77/15=7,45. Сумма расстояний между объектами, вошедшими в кластеры:  1∙2,83+1∙3,16+1∙3,16+1∙2,00+1∙3,61+1∙2,24=17,00.Среднее расстояние между объектами в кластерах = 17,00/6=2,83. Сумма расстояний между объектами, находящимися в разных кластерах:  (1-0)∙10,19+(1-0)∙12,17+(1-0)∙13,60++(1-0)∙8,94+(1-0)∙10,77+(1-0)∙12,53+ +(1-0)∙7,07+(1-0)∙9,06+ (1-0)∙10,44= 94,77. Среднее расстояние между объектами, находящимися в разных кластерах =94,77/9=10,53. Таким образом, мы убедились, что условия постановки задачи выполнены, т.е. среднее расстояние между элементами в кластерах более, чем в два с половиной раза меньше чем среднее расстояние между объектами: 7,45/2,83=2,63; а расстояние между объектами, находящимися в различных кластерах почти в полтора раза превышает среднее расстояние между объектами 10,53/7,45=1,41. Пример 5.6 Расстояние Хемминга. Ближайший сосед Требуется разделить шесть объектов на два кластера. Объекты – информационные системы характеризуются двумя признаками: Х1-среднее время решения одной задачи в минутах; Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы. Значения признаков Х1 и Х2 для шести объектов представлены в таблице 5.6.1. Таблица 5.6.1
Вычислены расстояния между объектами по формуле Хемминга по двум признакам. Проведение вычислений для второго и пятого объектов пояснено рис.5.6.1 и для второго и шестого объектов рис 5.6.2. Результаты вычислений расстояний по Хеммингу представлены в таблице 5.6.2.     10 Х2 8        6 4 d15 =|2-14|+|8-6|=14  2  2 4 6 8 10 12 14 Х1 Рис.5.6.1   10 Х2 8 6  4 2 d26 =|4-15|+|10-4|=17 2 4 6 8 10 12 14 Х1 Рис.5.6.2 Таблица 5.6.2
|