Задач. Задачи по статистике решённые. Пример задания 1
 Скачать 1.07 Mb.
|
|
c2 при которых гипотеза о подчинении исходных случайных чисел равномерному закону не отвергается, т.е. соблюдается условие: 0.1≤рр≤0.9. Таблица 2.1
Задание 1.3 Провести аппроксимацию пяти пар случайных чисел, представленных в таблице 3.1, линейной зависимостью  .Таблица 3.1
Экспериментальные точки, координаты которых представлены в таблице 3.1, представим в системе координат на рис.3.1.  у   9 • 7 • 4 • 2 • 1 • 1 2 3 4 5 х Рис.3.1 Для проведения аппроксимации проведём предварительные вычисления.             Вычислим коэффициент линейной корреляции.  По статистическим таблицам найдём критическое значение критерия Стьюдента tкрит=3,1814 при n-2=5-2=3 степенях свободы и рекомендуемому уровню значимости α=0,05. 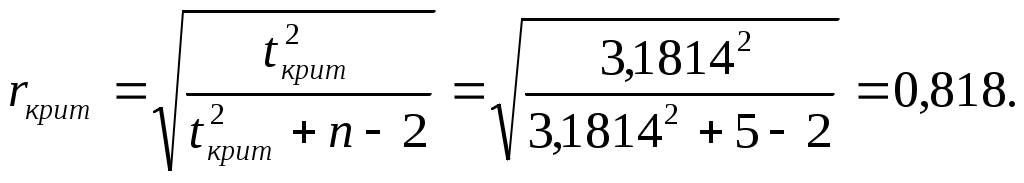 Ввиду того, что  делаем заключение, что корреляционная связь между переменными х и у является существенной и она может быть линейной.Вычислим коэффициенты линейной зависимости по формулам: 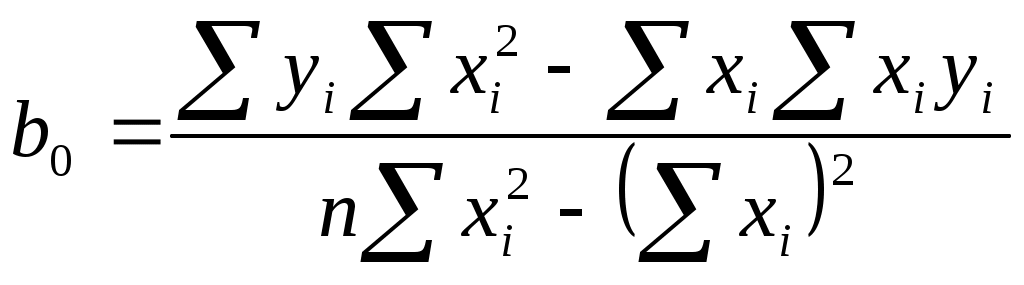 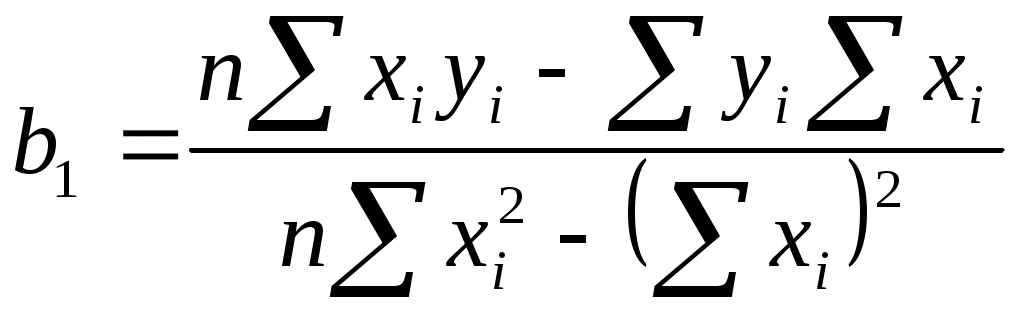   Таким образом, получили линейное уравнение регрессии:  По уравнению регрессии по двум точкам построим функцию в системе координат на рис.3.1 и вычислим значения функции по экспериментальным значениям аргумента х и разницу между экспериментальными и вычисленными значениями функции, которые представим в таблице 3.2. Таблица 3.2
Вычислим стандартную ошибку и отношение стандартной ошибки к среднему значению: 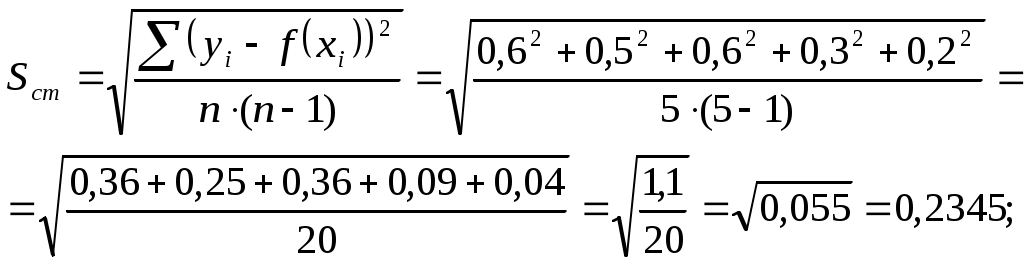  По отношению стандартной ошибки к среднему значению получен удовлетворительный результат, так как не превышено значение в 0.05. Проведём оценку уровня значимости коэффициентов уравнения регрессии по критерию Стьюдента: 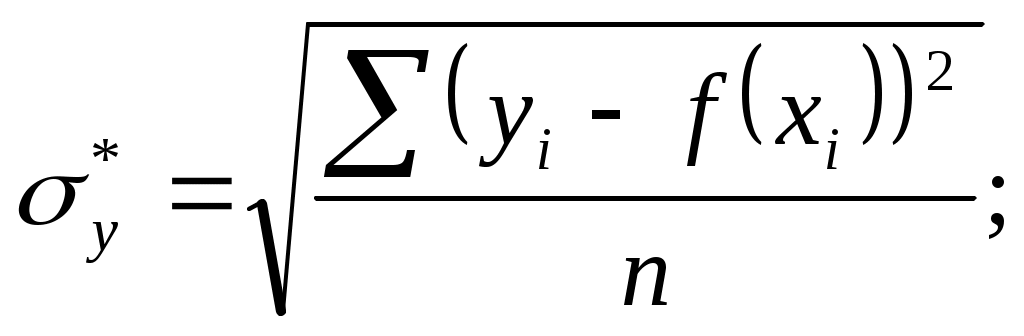  где      По статистической таблице находим критическое значение критерия Стьюдента tкрит=3,183 для  3 степеней свободы и рекомендуемого уровня значимости  =0,05. Отметим, что по уровню значимости для коэффици-ентов  и  получен удовлетворительный результат, так как они по асолютному значению превышают критическое значение.Проведём оценку качества полученного уравнения регрессии по показателям, вычисляемым на основе дисперсионного анализа:         Проверка:  Результат проверки – положительный, что свидетельствует о корректности проведённых вычислений. Вычислим критерий Фишера:  при двух степенях свободы:   По статистическим таблицам находим критическое значение критерия Фишера для рекомендуемого уровня значимости α=0.05  Так как вычисленное значение критерия Фишера превосходит критическое, то будем считать уровень значимости по критерию Фишера удовлетворительным.Вычислим коэффициент множественной детерминации:  для двух степеней свободы   По статистической таблице для уровня значимости 0,05 находим критическое значение коэффициента множественной детерминации:  Так как вычисленное значение коэффициента множественной детерминации превышает критическое значениe, то полученный результат по данному показателю будем считать удовлетворительным. Таким образом, все полученные расчётные показатели по оценке качества уравнения регрессии являются удовлетворительными, поэтому будем считать результаты аппроксимации приемлемыми. Задание 1.4 Пример 1.4.1 Провести оптимизацию графическим методом. 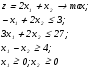 Приравняем целевую функцию нулю, неравенства заменим равенствами и затем представим их функциями х2отх1. х2=-2х1; х2= 1,5+0,5х1; х2=13,5-1,5х1; х2=-4+х1 и представим в системе координат на рис.4.1.  у (2)      9 8  (3)   6 4   2 ОДР    1 2 3 4 5 6 7 8 9 х Целевая функция Рис.4.1 Область допустимых решений (ОДР) ограничивается осью координат х1, ограничением (2) и ограничением (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (4;0) а последняя – максимума (9;0). В точке минимума z =8,в точке максимума z=18. Проверим выполнение всех ограничений в найденных точках. Для точки минимума -4+0<3 выполняется; 3·4+0<27 выполняется; 4-0=4 выполняется как равенство. Для точки максимума -9+0<3 выполняется; 3·9+0=27 выполняется как равенство; 9-0>4 выполняется. Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным. Отметим, что если какая-то проверяемая точка превращает неравенство в равенство, то данная точка принадлежит прямой линии, представляющей данное неравенство. В процессе оптимизации может оказаться, что какая-то точка лежит на пересечении двух, или большего количества прямых, то её координаты можно найти решением системы уравнений. Пример 1.4.2 Если в условиях примера 1.4.1 изменить третье неравенство на х1+х2≤4 то постановка задачи примет следующий вид: 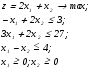 В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.2. у (2)       9 8 (3) 6  4    2 ОДРОДР  1 2 3 4 5 6 7 8 9 х Целевая функция Рис.4.2 Область допустимых решений (ОДР) ограничивается осью координат х1 и тремя ограничениями (1), (2) и (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (0;0) а последняя – точкой максимума (7;3). В точке минимума z =0,в точке максимума z=17. Проверим выполнение всех ограничений в найденных точках. Для точки минимума -0+0<3 выполняется; 0+0<27 выполняется; 0-0<4 выполняется. Для точки максимума -7+2·3<3 выполняется; 3·7+2·3=27 выполняется как равенство; 7-3=4 выполняется как равенство. Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным. Отметим, что если какая-то проверяемая точка превращает неравенство в равенство, то данная точка принадлежит прямой линии, представляющей данное неравенство. В процессе оптимизации может оказаться, что какая-то точка лежит на пересечении двух, или большего количества прямых, то её координаты можно найти решением системы уравнений. В нашем случае точка максимума лежит на пересечении ограничений (2) и (3). Покажем, что в данном случае её координаты можно найти решением уравнения х2=13,5-1,5·х1=-4+х1; откуда 2,5·х1=17,5; х1=17,5/2,5=7; х2=-4+7=3. Пример 1.4.3 В условиях примера 1.4.2 произведём преобразование, изменив ограничение (2). Тогда постановка задачи оптимизации примет следующий вид: 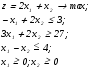 В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.3. у (2)      9  8 (3)   6 (1)    4 ОДР 2  1 2 3 4 5 6 7 8 9 10 11 х Целевая функция Рис.4.3 Область допустимых решений (ОДР) определяется тремя ограничениями (1), (2) и (3). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (6;4,5) а последняя – точкой максимума (11;7). В точке минимума z =16,5,в точке максимума z=28. Проверим выполнение всех ограничений в найденных точках. Для точки минимума -6+2·45=3 выполняется как равенство; 3·6+2·4,5=27 выполняется как равенство; 6-4.5<4 выполняется. Для точки максимума -11+2·7=3 выполняется как равенство; 3·11+2·7>27 выполняется; 11-7=4 выполняется как равенство. Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным. Пример 1.4.4 Изменим постановку задачи примера 1.4.1, изменив ограничения (1) и (3). 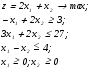 В этом случае произойдёт перемещение области допустимых решений как это показано на рис.4.4.  у     14 (2)  12 10  8 (3) 6 ОДР 4      2 1 2 3 4 5 6 7 8 9 х Целевая функция Рис.4.4 Область допустимых решений (ОДР) ограничивается осью координат у1, ограничением (1) и ограничением (2). Мысленно направим целевую функцию к ОДР, тогда первая точка их пересечения будет являться точкой минимума (0;1,5) а последняя – точкой максимума (6;4,5). В точке минимума z =3,в точке максимума z=16,5. Проверим выполнение всех ограничений в найденных точках. Для точки минимума 0+2·1,5=3 выполняется как равенство; 3·0+2·1,5<27 выполняется; 0-1,5<4 выполняется. Для точки максимума -6+2·4,5=3 выполняется как равенство; 3·6+2·4,5=27 выполняется как равенство; 6-4,5<4 выполняется. Таким образом, в точке минимума значение целевой функции меньше чем в точке максимума и все ограничения выполняются поэтому решение будем считать корректным. Отметим, что решение четырёх примеров позволило найти минимумы и максимумы целевой функции в четырёх различных ОДР, определяемых задаваемыми ограничениями. В остальных областях координатного пространства могут быть найдены только точки минимумов целевой функции, то есть решение будет неполным, ввиду того что области для поиска точек максимума являются расходящимися. Задание 1.5 Пример 1.5.1 Евклидово расстояние. Наиболее близкий сосед Требуется разделить шесть объектов на два кластера. Объекты – информационные системы характеризуются двумя признаками: Х1-среднее время решения одной задачи в минутах; Х2-количество задач, в решении которых было отказано ввиду перегрузки информационной системы. Значения признаков Х1 и Х2 для шести вариантов информационной системы представлены в таблице 5.1.1. Таблица 5.1.1
|
