Неопределенность на входе. Принятие решений при неопределённости и риске введение
 Скачать 165.09 Kb. Скачать 165.09 Kb.
|
|
1.1.2. Матрица потерь. Для того, чтобы попытаться ответить на вопрос, какие реше-ния всё же должны приниматься ЛПР в той или иной игре с природой (принятием реше-ния в условиях неопределенности), нам потребуется ещё одна матрица, называемая мат-рицей потерь (часто называемая также матрицей рисков и матрицейсожалений). Однако построение матрицы потерь значительно проще, чем построение платежной матрицы. Собственно говоря, она и строится непосредственно по платежной матрице. Рассмотрим ту же самую задачу продавца напитков, что и выше. Выберем в каждом столбце платеж-ной матрицы (см. Табл. 1.1) максимальный платеж. В первом столбце максимальный пла-теж равен 100, во втором столбце 420, в третьем 1000 и в четвертом 1340 (знаки доллара здесь опущены). Максимальное значение платежа при данном состоянии природы соответствует опти-мальному решению, если бы каким-то образом стало точно известным состояние приро-ды. Если бы было точно известно, что реализуется состояние природы С1, оптимальным было бы решение А1, если состояние С2 – также решение А1, если состояние С3 – решение А2, и если состояние С4 – решение А3. Действительно, если бы было точно известно, что в августе действительно будет холодно, то наилучшим решением в данной ситуации было бы закупить 1000 л напитков. И хотя получаемая при этом прибыль невелика и составляет всего $ 100, однако принятие других решений А2 и А3 приведет вообще к потерям (–$ 200 и –$ 500 соответственно) и мы сожалели бы о том, что не приняли решения А1. А если бы точно было известно, что в августе будет прохладно, оптимальным будет также решение А1 – закупить 1000 л напитков, потому что получаемая при этом прибыль ($ 420) выше прибыли $ 120 для решения А2, не говоря уже об убытках при принятии решения А3 (–$ 180). Точно также, если в действительности реализуется теплая погода, то оптимальным решением будет закупить партию объемом 2000 л, как приносящую наибольшую прибыль $ 1000, а если жаркая, то оптимальным решением (А3) будет закупить партию в 3000 л и получить максимальную прибыль $ 1340. Если же мы принимаем другие решения, то нам остаётся только сожалеть о том, что мы не приняли оптимального. Какое именно состояние природы реализуется в будущем, предсказать в точности не-возможно, однако для каждого из них можно найти оптимальное решение и вычислить, насколько оно будет отличаться от любого другого, неоптимального решения. Отличие оптимального решения от любого другого определяется величиной потерь от принятия неоптимального решения. Чем эта величина больше, тем больше наши потерянные воз-можности. Составим матрицу с теми же строчками и столбцами, что и в платежной матрице, т. е. как и выше, строки матрицы соответствуют решениям продавца, а столбцы – состояниям природы (см. Табл. 1.3). Для того, чтобы численно оценить потери для каждого решения, целесообразно рассмотреть отклонения получившихся доходов от максимально возмож-ного при данном состоянии природы. Поэтому в первый столбец запишем разницу в дохо-дах, получаемую между оптимальным (при данном состоянии природы) решением и теми доходами, которые продавец получит при других решениях. Поэтому при выборе альтер-нативы А2 отклонение составит 100 ‒ (‒200) = 300, а при выборе альтернативы А3 откло-нение составит 100 ‒ (‒500) = 600. Именно этих сумм продавец недосчитается по сравне-нию с оптимальным (в данном случае) решением А1 и именно об их потере он и будет сожалеть. Аналогично заполняются и другие столбцы, в которые вписываются разницы между доходами при оптимальном решении и остальными решениями. Таблица 1.3. Матрица потерь продавца прохладительных напитков
Легко понять, что все числа в матрице потерь неотрицательны и что в каждом столбце хотя бы один элемент равен 0. Этот ноль располагается в строке, которая соответствует оптимальному при данном состоянии природы решению. Вообще говоря, таких решений может быть несколько, однако в рассматриваемой ситуации все оптимальные решения единственны. В общем случае матрица потерь строится по платежной матрице (см. Табл. 1.2) аналогично. Она представляется следующим образом: Таблица 1.4. Общий вид матрицы потерь
Элементы rij матрицы потерь r определяются по элементам aij исходной платежной матрицы а по формулам aj= 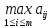 (j = 1, …, n), (1.2) (j = 1, …, n), (1.2)rij = aj ‒ aij (i = 1, …, m; j = 1, …, n). (1.3) Прежде чем переходить непосредственно к выбору оптимальной альтернативы в той или иной задаче вида, надо вычислить (найти, построить, определить) обе матрицы. 1.2. Основные методы принятия решений в условиях неопределённости Рассмотрим несколько методов принятия решений в условиях неопределенности, различающихся критериями, по которым определяются наилучшие решения: максиминный критерий (критерий Вальда); критерий минимаксного сожаления (критерий Сэвиджа); критерий Лапласа; максимаксный критерий. Изложение, как и в разделе 1.1, будем сопровождать тем же самым примером с про-давцом прохладительных напитков. Платежная матрица и матрица потерь для этой задачи уже известны. Они приведены в Табл. 1.1 и 1.3. 1.2.1. Максиминный критерий (критерий Вальда). Критерий Вальда называют еще критерием пессимизма, потому что он ориентируется при выборе решения на наступление наихудших условии. Критерий позволяет принимать такое решение, которое гарантирует некоторый выигрыш даже при наступлении самого неблагоприятного состояния природы, так что при реализации более благоприятных состояний природы ЛПР получит больший выигрыш. Применение максиминного критерия оправдано для осторожного, не склонного к риску ЛПР, а также в ситуациях, в которых получение отрицательного результата недо-пустимо, например, когда речь идет о безопасности людей и их здоровье. Другое хорошо известное название максиминного критерия – принцип гарантированного результата, так-же выражающее его суть. Приведем для удобства еще раз матрицу платежей для задачи продавца напитков (см. Табл. 1.1): Таблица 1.1. Платежная матрица продавца прохладительных напитков
Суть дела при максиминном критерии такова. Рассмотрим 1-ую альтернативу А1 и пос-мотрим, каков худший результат при этой стратегии. Худшим является случай состояния природы С1. Доход продавца составляет $ 100. При других состояниях природы его доход превосходит $ 100. Табл. 1.1 также ясно показывает, что худший результат при альтерна-тиве А2 равен $ ‒200, при альтернативе А3 он равен $ ‒500. Максиминный критерий рекомендует выбрать альтернативу А1, при которой результат при самом неблагоприят-ном стечении обстоятельств (состоянии природы) будет лучше, чем при выборе любых других альтернатив. При любом другом состоянии природы доход продавца не может быть меньшим, чем $ 100, если он выбрал альтернативу А1. Именно поэтому максимин-ный критерий часто называется принципом гарантированного результата. В общем случае определение наилучшего решения по критерию Вальда состоит из следующих этапов: построить платежную матрицу; в каждой строке платежной матрицы (см. Табл. 1.2), соответствующей определенному возможному решению Аi, выбрать минимальную величину платежа vi = 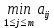 (i = 1, …, m); (i = 1, …, m); из всех найденных минимальных платежей vi (i = 1, 2, …, т) выбрать максималь-ное значение vmax = max1≤ i ≤ m vi; решение, которому соответствует найденная на предыдущем этапе величина vmax, и будет наилучшим. 1.2.2. Критерий минимаксных потерь (критерий Сэвиджа). Критерий Сэвиджа, как и критерий Вальда, относится к пессимистичным критериям. ЛПР, применяющий критерий Сэвиджа, исходит того, что всегда следует ожидать наступление наихудшего состояния природы, или хотя бы готовиться к нему. Однако в отличие от критерия Вальда, в котором по платежной матрице сначала ищется минимальный платеж, а среди них ‒ максимальный, критерий Сэвиджа оперирует матрицей потерь и в ней сначала определя-ется максимальная потеря, а среди них ‒ минимальная. Наилучшее решение по критерию Сэвиджа гарантирует получение наименьших потерь в наихудших условиях. Другими сло-вами, критерий Сэвиджа выбирает то решение, при котором минимизируются потери при возможном наступлении наихудших состояний природы Приведем для удобства еще раз матрицу потерь для задачи продавца напитков: Таблица 1.3. Матрица потерь продавца прохладительных напитков
Суть дела при критерии Сэвиджа такова. Рассмотрим альтернативу А1 и посмотрим, како-ва максимальная потеря при этой альтернативе. Максимальной ($ 840) оказывается потеря при состоянии природы С4. При альтернативе А2 максимальная потеря равна 340. При альтернативе А3 максимальная потеря равна 600. Напомним, что потеря – это разность между максимальным доходом при некотором состоянии природы и реальным доходом, полученным при использовании некоторой альтернативы. Из трёх потерь: $ 840, $ 340 и $ 600 ‒ минимальной является потеря $ 340 при выборе альтернативы А2. Процедура применения минимаксного критерия Сэвиджа содержит следующие шаги: построить платежную матрицу; по платежной матрице построить матрицу потерь; в каждой строке матрицы потерь, соответствующей определенному возможному решению Аi, выбрать максимальную величину потери vi = 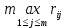 (i = 1, …, n); (i = 1, …, n); из всех найденных максимальных потерь vi (i = 1, 2, …, т) выбрать минимальное значение vmin = min1≤i≤mvi; решение, которому соответствует найденная на предыдущем этапе величина vmax, и будет наилучшим. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
