Неопределенность на входе. Принятие решений при неопределённости и риске введение
 Скачать 165.09 Kb. Скачать 165.09 Kb.
|
|
1.4. Теорема о минимаксе и седловые точки В этом разделе мы вернёмся к исходной постановке задачи оптимизации в условиях неопределённости, выраженной формулой (В2) f(u,) → 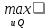 (1.6) (1.6)Для удобства чтения эта формула повторена здесь. В ней заранее неизвестное воздейс-твие, принадлежащее некоторому множеству G, которое во многих случаях можно считать известным (в отличие от его конкретного элемента ). Именно такая постановка была рассмотрена выше в разделах 1.1 – 1.4. Для продавца прохладительных напитков в качестве множества G выступает множество возможных состояний погоды в августе {холодно, прохладно, тепло, жарко}. Рассмотрим общий случай. Выбирая произвольно uQ, получаем выигрыш x = f(u,), где может быть любым значением неконтролируемой переменной. Самое меньшее, что мы можем при этом получить – это зависящий только от u выигрыш x(u) = 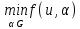 . (1.7) . (1.7)Обозначим через u* то значение контролируемой переменной u, при котором левая часть (1.7) x(u) достигает максимума, а само это значение xобозначим через x*: x* = x(u*) = 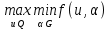 . (1.8) . (1.8)Вход u* в пункте 1.2 назван гарантирующей стратегией*, а соответствующее максимальное значение x* = x(u*) гарантированным результатом. Смысл этих названий состоит в следующем: выбор u = u* при любом значении неконтролируемого входа гарантирует значение целевой функции f(u,), не меньшее, чем x*. Для получения гарантирующей стратегии и гарантированного результата надо сделать следующее. 1. Вычислить x(u) = 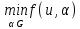 (см. (1.7)) для любого uQ. (см. (1.7)) для любого uQ. 2. Вычислить x* = 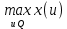 (cм. (1.8)). (cм. (1.8)). Так, x* является гарантированным результатом, а то значение контролируемой переменной u, на котором достигается максимум в (1.8), является гарантирующей стратегией u*. Как видим, необходимо решить не одну оптимизационную задачу, а целое семейство таких задач. Это естественная расплата за неопределённость и, к сожалению, далеко не единственная. Главный же недостаток гарантированного результата это его неоптимальность. Грубо говоря, при получении оценки x* (см. формулы (1.7) и (1.8)) мы «закладывались» на самый худший случай (брали в (1.7) минимум функции по ). Житейский опыт подсказывает, что такое поведение, как правило, далеко не оптимально. А что же будет, если рискнуть и выбрать u≠ u*? Может ведь случиться и так, что неконтролируемое значение окажется как раз таким, которое минимизирует f(u,), и при этом мы получим результат x(u), ещё худший, чем x*. Все эти рассуждения можно подытожить пессимистической пословицей: кто не рискует, тот не ужинает с коньячком, а кто рискует, тот совсем не ужинает. То, что мы перешли от формальной постановки к содержательным рассуждениям, т.е. то, что в условиях неопределённости задача оптимизации (1.6) по существу перестает быть формальной, связано с более глубокими причинами, о которых будет сказано в части 4. Слегка видоизменим постановку. Пусть (как это действительно иногда бывает) мы можем принять решение, предварительно выяснив ситуацию. Формально это означает, что мы выбираем u, уже зная . Естественно, u выбирается из условия x() = 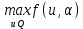 . (1.9) . (1.9)То значение u, на котором достигается максимум в правой части (1.9), обозначим через u(); соответствующее значение x обозначено в (1.9) через x(). Можно считать, что x() это наилучший результат, которого мы можем достичь, если неконтролируемый фактор принимает некоторое значение G. При этом в худшем случае мы получим x0 = 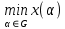 = = 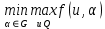 . (1.10) . (1.10)В этой ситуации гарантирующей является уже не одна стратегия u, а вся функция u(), поскольку управление u() обеспечивает наилучший результат при каждом значении . Оказывается, что в рассматриваемой ситуации, когда известно заранее, выигрыш всегда не меньше, чем тогда, когда заранее неизвестно. Формально это означает, что x0 = 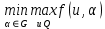 ≥ ≥ 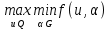 = x*. (1.11) = x*. (1.11) Имеет место Утверждение 1. (Теорема о минимаксе). Пусть A и B два множества, F(x,y) – любая функция от двух переменных, определённая при всех xA и yB. Тогда 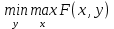 ≥ ≥ 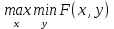 . (1.12) . (1.12)Доказательство. Пусть (x, y) произвольная пара переменных. Ясно, что 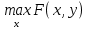 ≥ F(x, y). (1.13) ≥ F(x, y). (1.13)Левая и правая части (1.13) при фиксированном xявляются функциями от y. Обозначим их через φ1(y) и φ2(y). Ясно, что из φ1(y) ≥ φ2(y) следует, что 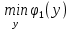 ≥ ≥ 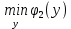 откуда с учётом определения φ1(y) и φ2(y) получаем 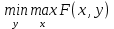 ≥ ≥ 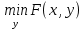 . (1.14) . (1.14) Неравенство (1.14) верно при любых x, причем его левая часть от x не зависит. Поэтому оно остаётся верным, если в правую часть подставить то значение x, которое её максимизирует, т.е. 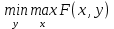 ≥ ≥ 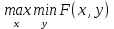 , что совпадает с (1.12). , что совпадает с (1.12). В доказательстве предполагалось, что все максимумы и минимумы достигаются. Это не очень существенное ограничение, учитывая, что на компактном (замкнутом и ограниченном) множестве любая непрерывная функция достигает максимального и минимального значений. Однако оно останется верным для произвольных функций, если минимум заменить на инфинум, а максимум – на супремум. Неравенство (1.12) очевидно, эквивалентно (1.11) при F(x,y) = f(u,), x = u, y = , A = Q и B = G. Разница x0 x* это и есть наша плата за незнание ситуации. Именно ради этой разницы и работают все разведки мира. Подчеркнём ещё раз выгоду (и иногда ог-ромную) приносит только знание о неконтролируемых факторах, даже без малейшей возможности влиять на них. «Знал бы прикуп, жил бы в Сочи». Пример 1.2. Пусть f(u, α) = –(u – α)2, множества возможных значений Q и G – множества всех действительных чисел от –∞ до ∞. Найдём для этой функции 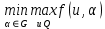 и и 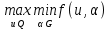 . .1. При любом α выражение –(u – α)2 достигает максимума, равного 0, при u = α. Поэтому 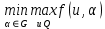 = minα 0 = 0. = minα 0 = 0.2. При любом uвыражение –(u – α)2 может быть сколь угодно большим по модулю отрицательным числом. Можно считать, что при любом u 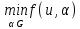 = –∞, откуда = –∞, откуда 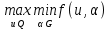 = –∞. = –∞.Пример 1.3. Пусть теперь f(u, α) = (u – α)2 при Q = [0, 100], G = [0, 100]. Найдём для этой функции 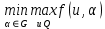 и и 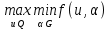 . .1. Определим максимум выражения (u – α)2 в зависимости от α. Легко видеть, что u(α) = 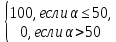 , откуда , откуда 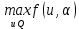 = =  . .Поэтому 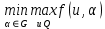 достигается при α = 50, т.е. достигается при α = 50, т.е. 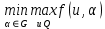 = 502 = 2500. = 502 = 2500.2. Определим минимум выражения (u – α)2 в зависимости от u. При любом uминимум (u – α)2 достигается при α= u; он равен 0. Ясно, что 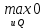 = 0, т.е. = 0, т.е. 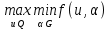 = 0. = 0. Пример 1.4. Попытаемся найти гарантирующую стратегию и гарантированный ре-зультат для функции f(u, α) из примера 1.2. В данном случае f(u, α) = –(u – α)2, множества возможных значений Q и G – множества всех действительных чисел от –∞ до ∞. В соот-ветствии с описанным выше методом находим x(u) = 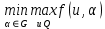 = = 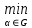 –(u – α)2 = –∞. –(u – α)2 = –∞.Поэтому в данном случае гарантирующая стратегия и гарантированный результат не опре-делены. Пример 1.5. Найдём гарантирующую стратегию и гарантированный результат для функции f(u, α) из примера 1.3. В соответствии с описанным выше методом находим x(u) = 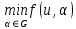 = = 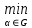 (u – α)2 = 0 (при α= u). (u – α)2 = 0 (при α= u).Ясно, что гарантирующей является любая стратегия u, поскольку гарантированный результат 0 обеспечивается при любом u. 1.4.1. Седловые точки. Пусть для некоторой функции f(x, y) от двух переменных в формуле (1.12) имеет место равенство:  f(x, y) = f(x, y) =  f(x, y). (1.15) f(x, y). (1.15)Это значит, что в некоторой точке (x*, y*), где x*A, y*B  f(x, y) = f(x*, y*) = f(x, y) = f(x*, y*) =  f(x, y). (1.16) f(x, y). (1.16)Точки (x*, y*), удовлетворяющие условию (1.16), называются седловыми точками. Это название связано с их геометрической интерпретацией: поверхность функции z= y2 – x2, для которой точка (0, 0) удовлетворяет условиям (1.16), напоминает седло (см. рис. 1). 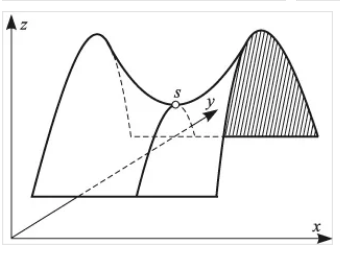 Рис. 1. Седловая точка Имеют место следующие утверждения. Утверждение 2а. Пусть для некоторых множеств X и Y и некоторой функции f(x, y), определённой при всех xX и yY, точки (x1, y1) и (x2, y2) являются седловыми, т.е. удовлетворяют условиям (1.16). Тогда f (x1, y1) =f(x2, y2), (1.17) т.е. значения функции во всех седловых точках (если их больше одной) совпадают. Утверждение 2б. Пусть (x1, y1) и (x2, y2) – две седловые точки. Тогда (x1, y2) и (x2, y1) также являются седловыми точками. Утверждение 2в. Для любой седловой точки (x*, y*), любого xX и любого yY имеют место неравенства f(x, y*) ≤ f(x*, y*) ≤ f(x*, y). (1.18) Утверждение 2г. Пусть для некоторых множеств Xи Yи некоторой функции f(x, y), определённой при всех xX и yY, существует точка (x*,y*), для которой при любом xX и любом yY выполнено (1.18). Тогда для этой функции f(x, y) и точки (x*,y*) выполнено равенство (1.16), т.е. точка (x*, y*) является седловой точкой. Пример 1.6. Нахождение минимакса и максимина. Продемонстрируем вычисление  f(x,y) и f(x,y) и  f(x,y). Сначала введём некоторые необходимые понятия и обозначения. Будем рассматривать функции f(x, y), такие, что f(x,y) = φ(z), где z = |x–y|, φ(z) – непрерывная монотонно возрастающая функция, определённая при всех z ≥ 0, и φ(0) = 0, Например, к таким функциям относятся f(x,y) = (x– y)2, f(x, y) = f(x,y). Сначала введём некоторые необходимые понятия и обозначения. Будем рассматривать функции f(x, y), такие, что f(x,y) = φ(z), где z = |x–y|, φ(z) – непрерывная монотонно возрастающая функция, определённая при всех z ≥ 0, и φ(0) = 0, Например, к таким функциям относятся f(x,y) = (x– y)2, f(x, y) =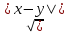 , f(x, y) = arctg(|x–y|), и пр. , f(x, y) = arctg(|x–y|), и пр.Далее, будем предполагать, что оба множества Xи Y являются отрезками на числовой оси: X = [a, b], Y = [c, d]. Величины  f(x, y) и f(x, y) и  f(x, y) существенно зависят от взаимного расположения этих отрезков. Далее рассматриваются два случая с номерами 2 и 3. Нумерация охватывает все случаи взаимного расположения двух отрезков. Она начинается со случая a<b≤ c<d(отрезок Y = [c, d] расположен справа от отрезка X = [a, b]). Заканчивается нумерация случаем c<d≤ a<b, когда отрезок Y = [c, d] расположен слева от отрезка X = [a, b]. f(x, y) существенно зависят от взаимного расположения этих отрезков. Далее рассматриваются два случая с номерами 2 и 3. Нумерация охватывает все случаи взаимного расположения двух отрезков. Она начинается со случая a<b≤ c<d(отрезок Y = [c, d] расположен справа от отрезка X = [a, b]). Заканчивается нумерация случаем c<d≤ a<b, когда отрезок Y = [c, d] расположен слева от отрезка X = [a, b].Случай 2: a< 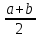 ≤ c< b< d; отрезки [a, b] и [c, d] пересекаются и общими точками являются все точки отрезка [c, ≤ c< b< d; отрезки [a, b] и [c, d] пересекаются и общими точками являются все точки отрезка [c, 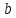 ], но при этом середина ], но при этом середина 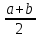 отрезка [a, b] не является внутренней точкой отрезка [с, b], т.е. не принадлежит ему или совпадает с концом с. отрезка [a, b] не является внутренней точкой отрезка [с, b], т.е. не принадлежит ему или совпадает с концом с.1) g(x) = 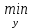 f(x,y) = f(x,y) = 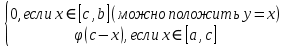 . .Далее,  f(x,y) = f(x,y) = 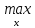 g(x) = φ(c–a). Гарантирующей стратегией является a, гаранти-рованным результатом φ(c– a). g(x) = φ(c–a). Гарантирующей стратегией является a, гаранти-рованным результатом φ(c– a).2) h(y) = 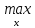 f(x,y) = φ(y–a) (a– самая далёкая от любой точки y[c, d] точка на [a, b]). f(x,y) = φ(y–a) (a– самая далёкая от любой точки y[c, d] точка на [a, b]).Далее,  f(x,y) = f(x,y) = 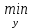 h(y) = h(y) = 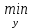 φ(y– a) = φ(c– a). φ(y– a) = φ(c– a).Сравнение. В данном случае  f(x,y) = φ(c–a) = φ(a–c) = f(x,y) = φ(c–a) = φ(a–c) = f(x,y). Поэтому седловой точкой будет точка (a, c). f(x,y). Поэтому седловой точкой будет точка (a, c).Случай 3: a< c< 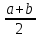 < b< d; отрезки [a, b] и [c, d] пересекаются и общими точками являются все точки отрезка [c, b], но при этом середина < b< d; отрезки [a, b] и [c, d] пересекаются и общими точками являются все точки отрезка [c, b], но при этом середина 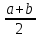 отрезка [a, b] принадлежит пересечению [c, b] и является его внутренней точкой (в отличие от случая 2). отрезка [a, b] принадлежит пересечению [c, b] и является его внутренней точкой (в отличие от случая 2). 1) g(x) = 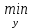 f(x, y) = f(x, y) = 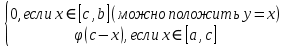 Далее,  f(x, y) = f(x, y) = 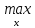 g(x) = φ(с–a). Гарантирующей стратегией является a, гаранти-рованным результатом φ(c– a). g(x) = φ(с–a). Гарантирующей стратегией является a, гаранти-рованным результатом φ(c– a).2) h(y) = 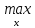 f(x, y) = f(x, y) = 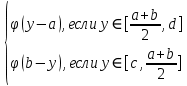 . . Далее,  f(x, y) = f(x, y) = 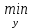 h(y) = φ( h(y) = φ( 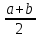 – a) = φ( – a) = φ(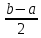 ). ).Сравнение. В данном случае  f(x,y) = φ(c–a), f(x,y) = φ(c–a),  f(x,y) = φ( f(x,y) = φ(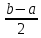 ) = φ(b – ) = φ(b – 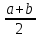 ). Так как в данном случае ). Так как в данном случае 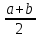 > c, то b–c < b – > c, то b–c < b – 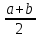 , откуда φ(b–c) < φ(b – , откуда φ(b–c) < φ(b – 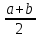 ) и ) и  f(x, y)< f(x, y)< f(x, y). Таким образом, седловой точки в данном случае нет. f(x, y). Таким образом, седловой точки в данном случае нет. |
