|
|
Неопределенность на входе. Принятие решений при неопределённости и риске введение
1.5. Задания
1. Задачи оптимизации заданы платежными матрицами, а различные сценарии соот-ветствуют различным состояниям природы. Найти решения, используя 4 метода, описан-ные в разделе 1.2. Данные в таблицах даны в тысячах долларов. Номера вариантов напи-саны в левом верхнем углу таблиц. Для образца см. раздел 1.2.
01
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
–11
|
18
|
14
|
26
|
2
|
27
|
10
|
–12
|
13
|
3
|
13
|
–21
|
35
|
23
|
02
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
8
|
–15
|
20
|
30
|
2
|
24
|
22
|
–18
|
65
|
3
|
–21
|
30
|
25
|
15
|
03
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
11
|
12
|
23
|
27
|
2
|
–28
|
25
|
20
|
14
|
3
|
22
|
17
|
19
|
–10
|
04
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
25
|
19
|
21
|
14
|
2
|
–18
|
–30
|
19
|
–15
|
3
|
30
|
25
|
30
|
15
|
05
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
–10
|
27
|
37
|
14
|
2
|
12
|
–14
|
27
|
–12
|
3
|
16
|
24
|
–14
|
25
|
06
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
8
|
–13
|
24
|
24
|
2
|
30
|
15
|
–27
|
26
|
3
|
–22
|
22
|
31
|
13
|
07
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
15
|
24
|
234
|
–23
|
2
|
–22
|
26
|
22
|
15
|
3
|
0
|
–13
|
24
|
22
|
08
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
–12
|
14
|
25
|
8
|
2
|
25
|
10
|
–27
|
20
|
3
|
18
|
–12
|
14
|
17
|
09
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
19
|
–16
|
25
|
19
|
2
|
10
|
8
|
18
|
30
|
3
|
–20
|
30
|
15
|
21
|
10
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
15
|
20
|
25
|
–19
|
2
|
15
|
21
|
–18
|
30
|
3
|
27
|
–10
|
19
|
20
|
11
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
8
|
15
|
20
|
30
|
2
|
24
|
22
|
18
|
–96
|
3
|
21
|
–30
|
25
|
15
|
12
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
25
|
15
|
–25
|
10
|
2
|
–20
|
9
|
27
|
14
|
3
|
20
|
–19
|
19
|
15
|
13
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
25
|
19
|
21
|
–14
|
2
|
18
|
30
|
19
|
15
|
3
|
30
|
–25
|
30
|
15
|
14
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
16
|
30
|
25
|
18
|
2
|
18
|
15
|
24
|
15
|
3
|
–27
|
26
|
6
|
–90
|
15
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
–13
|
24
|
24
|
16
|
2
|
15
|
27
|
–26
|
8
|
3
|
22
|
31
|
13
|
30
|
16
|
Стратегия
|
Сценарий 1
|
Сценарий 2
|
Сценарий 3
|
Сценарий 4
|
1
|
27
|
–15
|
34
|
21
|
2
|
–15
|
30
|
20
|
15
|
3
|
25
|
23
|
–13
|
29
|
2. Нахождение минимакса и максимина. Эта задание является продолжением при-мера 1.6. В тех же условиях надо найти  f(x,y) и f(x,y) и  f(x,y) при всех расположе-ниях отрезков X = [a, b], Y = [c, d]. Результаты надо занести в строки таблицы, которые соответствуют всем расположениям отрезков. Ситуации в строках 2 и 3 были проанализи-зированы в примере 5. Несколько неравенств в строках 6 – 9 означают их одновременное выполнение. f(x,y) при всех расположе-ниях отрезков X = [a, b], Y = [c, d]. Результаты надо занести в строки таблицы, которые соответствуют всем расположениям отрезков. Ситуации в строках 2 и 3 были проанализи-зированы в примере 5. Несколько неравенств в строках 6 – 9 означают их одновременное выполнение.
№№
п.п.
|
Расположение
отрезков
|
Maximin
|
Minimax
|
Оптимальные
значения x*, у*
|
1
|
a<b≤ c<d
|
|
|
|
2
|
a<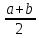 ≤ c<b <d ≤ c<b <d
|
φ(c– a)
|
φ(c– a)
|
a, c, +
|
3
|
a<c<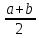 <b <d <b <d
|
φ(c– a)
|
φ(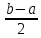 ) )
|
a,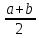 , – , –
|
4
|
c≤ a, b≤ d
|
|
|
|
5
|
a=с, b = d
|
|
|
|
6
|
a≤ с, d≤b;
c–a ≥ b–d;
с ≤ 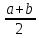 ≤d ≤d
|
|
|
|
7
|
a≤ с, d≤b;
c–a≤b–d;
с ≤ 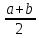 ≤d ≤d
|
|
|
|
8
|
a≤ с, d≤b;
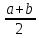 ≤c ≤c
|
|
|
|
9
|
a≤ с, d≤b;
d≤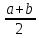
|
|
|
|
10
|
c<a<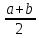 <d<b <d<b
|
|
|
|
11
|
c<a<d ≤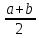 <b <b
|
|
|
|
12
|
c<d≤a<b
|
|
|
|
Знак + в последнем столбце ставится тогда и только тогда, когда имеется седловая точка. Её компоненты указываются в этом же столбце. При отсутствии седловой точки там записаны значения, на которых достигаются внешние экстремумы в формулах для максимина и минимакса.
2. Теоретические задачи
1. Доказать утверждение 2а
2. Доказать утверждение 2б
3. Доказать утверждение 2в
4. Доказать утверждение 2г
5. Может ли у функции быть ровно три седловых точки? Доказать или привести пример.
6. Есть ли седловая точка у функции x2y2 ?
7. Есть ли седловая точка у функции y2x 2 ?
8. В каком месте доказательства утверждения 1 используется то, что функция F(x,y) определена при всех xA и yB?
9. Остаётся ли верным утверждение 1, если функция F(x,y) определена на произвольном подмножестве множества AB? Доказать или привести пример.
1. Рубчинский А.А. Методы и модели принятия управленческих решений. – М. Юрайт, 2014. 526 стр.
|
|
|
 Скачать 165.09 Kb.
Скачать 165.09 Kb. f(x,y) и
f(x,y) и  f(x,y) при всех расположе-ниях отрезков X = [a, b], Y = [c, d]. Результаты надо занести в строки таблицы, которые соответствуют всем расположениям отрезков. Ситуации в строках 2 и 3 были проанализи-зированы в примере 5. Несколько неравенств в строках 6 – 9 означают их одновременное выполнение.
f(x,y) при всех расположе-ниях отрезков X = [a, b], Y = [c, d]. Результаты надо занести в строки таблицы, которые соответствуют всем расположениям отрезков. Ситуации в строках 2 и 3 были проанализи-зированы в примере 5. Несколько неравенств в строках 6 – 9 означают их одновременное выполнение.
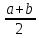 ≤ c<b <d
≤ c<b <d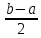 )
)