Неопределенность на входе. Принятие решений при неопределённости и риске введение
 Скачать 165.09 Kb. Скачать 165.09 Kb.
|
|
приНЯТИЕ РЕШЕНИЙ ПРИ НЕОПРЕДЕЛЁННОСТИ И РИСКЕ Введение В книге Герба Коэна «Обо всём можно договориться» утверждается: «Успешный под-ход к переговорам заключается в выяснении того, что в действительности необходимо противной стороне, и в доведении до её сознания того, каким образом она могла бы до-биться желаемого, не мешая мне получить свое». Эта цитата определяет очень разумный подход к взаимодействию участников с несовпадающими интересами, фокусирующийся на сотрудничестве, а не на соперничестве. Мы видим, что взаимодействия самого различ-ного рода, в которых в той или иной степени присутствуют и конфликты, и сотрудничест-во, встречаются постоянно. Они случаются и в нашей повседневной жизни, и в професси-ональной деятельности, и в окружающей нас действительности. Деление наследства или имущества при разводе, согласование различных точек зрения при принятии решений, спортивные соревнования и творческие конкурсы, выделение квот партиям или регионам в выборном органе, распределение различных видов работ между сотрудниками, доступ к компьютерным ресурсам при работе операционных систем и пользовательских программ, борьба за существование между хищниками и жертвами, переговоры о разоружении меж-ду супердержавами – всё это примеры взаимодействий, естественно сочетающих кон-фликты и сотрудничество. Важность и распространенность таких взаимодействий уже с давних пор привлекали внимание представителей различных видов профессиональной деятельности – математи-ков, управленцев, психологов, политологов, социологов, военных и других специалистов. На многочисленные ситуации такого типа естественно смотреть с двух разных точек зре-ния, которые условно можно назвать внутренней и внешней. С внутреннейточки зрения мы ассоциируем себя с одним из участников взаимодействия (или же на самом деле являемся им), пытаясь добиться наилучших для этого участника результатов, при том, что действия других участников (также преследующих свои цели) от нас не зависят. В силу такой точки зрения эта проблематика ориентирована больше на конфликты, чем на сот-рудничество. Она относится к теории игр, хорошо и подробно исследована, имеет много-численные приложения в самых разных реальных ситуациях. С внешнейточки зрения мы ассоциируем себя не с одним из участников взаимодействия, а с людьми и (или) ведомст-вами, организующими такое взаимодействие и разрабатывающими правила, в рамках ко-торых оно и проистекает. При этом предполагается, что результат взаимодействия всех участников, преследующих свои индивидуальные цели, будет достаточно разумным с более общей точки зрения, которая больше ориентирована на сотрудничество, чем на кон-фликт. Люди и организации, заинтересованные в результатах подобных взаимодействий и разрабатывающие их правила, иногда называются метаигроками, что подчеркивает их особую – по сравнению с остальными участниками – роль. В отличие от теории игр, общей теории взаимодействия с указанной точки зрения нет, однако есть важные результаты, полученные в рамках отдельных направлений. Достаточ-но известным примером такого рода постановок служит синтез механизмов в институцио-нальной экономике, когда игроками выступают экономические агенты, а в роли метаигро-ка, определяющего правила их взаимодействия, – государство (в лице соответствующих властных структур). Однако с такой точки зрения можно рассмотреть и многие другие процессы и явления в самых различных сферах. Примеры такой постановки – выработка правил агрегации индивидуальных предпочтений, разработка систем пропорционального представительства, правила справедливого дележа, алгоритмы предоставления вычисли-тельных ресурсов процессам в современных ЭВМ и многие другие ситуации, связанные с разработкой оптимальных или хотя бы разумных правил взаимодействия участников. Некоторые из этих вопросов наряду с более традиционными постановками теории игр и составляют материал данного небольшого пособия. Остановимся кратко на формальном описании рассматриваемой проблематики. В хорошо известной задаче оптимизации числовой функции f(u) → maxuQ, (В1) значение целевой функции f(u) однозначно определяется по любому варианту u из мно-жества Q допустимых вариантов. Однако во многих реальных ситуациях это предположе-ние не выполняется, и выход системы существенно зависит не только от воздействия u, контролируемого лицом, принимающим решения (далее для краткости ЛПР), но и от не-контролируемых факторов. Для ситуаций описанного типа уже довольно давно разработа-на формальная модель. Именно, целевую функцию записывают в виде x = f(u,), где некоторое воздействие (или набор воздействий), которое заранее неизвестно и не может быть контролируемым. Однако от этого воздействия , которое мы не контролируем, существенно зависит результат f(u,) наших контролируемых действий u. При этом исходная задача (В1) превращается в другую задачу: f(u,) → maxuQ, (В2) где заранее неизвестное воздействие. Различия между задачами (В1) и (В2) очень существенны. В первую очередь бросается в глаза, что задача (В2) не является формально поставленной. Действительно, как можно оптимизировать функцию, когда нам неизвестны значения части переменных? Поэтому предлагаются более конкретные постановки, предположения о неконтролиру-емых факторах и определения оптимальности. Эти предположения приводят к различным классам задач, относящихся к широко распространенным ситуациям подобного типа. Материал пособия структурирован в соответствие с рассматриваемыми классами за-дач. В 1-ой главе «Оптимизация в условиях неопределённости и риска» рассмотрены зада-чи вида (В2), в которых либо не делается совсем никаких предположений о неконтролиру-емых факторах , либо делаются предположения об их стохастическом характере. Пере-ход к формальному анализу ситуаций достигается путём различных расширений самого понятия оптимальности в задачах вида (В2). Во 2-ой главе «Элементы теории игр» предполагается, что исходная ситуация описы-вается уже не одной функцией, а семейством функций, соответствующим различным ЛПР. Каждый из них стремится максимизировать «свою» целевую функцию Fi(u1, u2, …, un) → 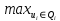 (i = 1, 2, …, n), (В3) (i = 1, 2, …, n), (В3)где n – общее число ЛПР, Qi – множество возможных действий i-го ЛПР, а каждая из функций Fi зависит, вообще говоря, от действий всех ЛПР, а не только от действий од-ного из них. В подобных ситуациях ЛПР называются игроками, элементы множества Qi – стратегиями i-го игрока, а целевые функции Fi– его функциями выигрыша. Поведение игроков при заданных множествах стратегий Qi и функциях выигрыша Fi (i = 1, 2, …, n) хорошо исследовано в рамках теории игр. Эта же терминология часто используется при описании задачи оптимизации (В2), рассмотренной в 1-ой главе. Она называется «игрой с природой», тем самым подчеркивая наличие только одного ЛПР, стремящегося к достижению своей цели. У природы цели нет! В 3-ей главе «Организация коллективного взаимодействия» представлены результаты анализа взаимодействия участников с вышеупомянутой внешней точки зрения в несколь-ких достаточно известных и практически интересных ситуациях принятия коллективных решений. Последний термин используется, чтобы подчеркнуть наличие нескольких ЛПР, принимающих решения хотя и независимо друг от друга, но с учетом действий остальных участников (игроков). Глава 1. Оптимизация в условиях неопределённости и риска 1.1. Формализация задачи. Платежная матрица и матрица потерь. 1.2. Основные методы принятия решений в условиях неопределённости 1.2.1. Максиминный критерий (критерий Вальда) 1.2.2. Критерий минимаксного риска (критерий Сэвиджа) 1.2.3. Критерий Лапласа 1.2.4. Максимаксный критерий 1.3. Принятие решений в условиях риска 1.4. Теорема о минимаксе 1.4. Задания В 1944 году уже не очень молодой и не слишком известный бизнесмен Пол Гетти взял концессию на кусок побережья Персидского залива в Саудовской Аравии. Он наде-ялся найти крупное месторождение нефти. Надежды были не безосновательны: в этом районе уже нашли нефть, и по мнению Пола Гетти, который получил геологическое обра-зование, нефть должна была найтись и на его участке. Он развернул разведочное бурение. Прошло несколько месяцев, было пробурено несколько десятков скважин, почти все имев-шиеся у Гетти деньги были потрачены, а нефти всё не было. Казалось, что надо немедлен-но прекратить все работы, чтобы избежать полного банкротства и спасти хоть какие-то деньги. Но Гетти упрямо продолжал работы. И этот риск оправдал себя. Когда денег оста-валось только на две недели, из очередной скважины хлынул фонтан нефти. Через несколько лет Пол Гетти стал самым богатым человеком на Земле. Когда один журналист сказал ему, что если разделить все его деньги между жителями нашей планеты, то у каждого будет по 100 долларов, Гетти ответил, что к концу того же дня все эти деньги перейдут от тех, кто беднее, к тем, кто богаче, т.е. это практически не улучшит жизнь лю-дей. Это и есть социальная ответственность бизнеса!3,, Описанная абзацем выше ситуация и есть игра с природой – в прямом смысле. Ре-шением Гетти был выбор места для бурения. А результат – наличие или отсутствие нефти в данной скважине – зависел от природы, т.е. от не контролируемой единственным игро-ком субстанции. Такого рода ситуациям и посвящена настоящая глава. Напомним (см. введение) рассматриваемую формальную модель. Целевую функцию записывают в виде x = f(u,), где некоторое воздействие (или набор воздействий), которое заранее неизвестно и не может быть контролируемым. Однако от этого воздейст-вия , которое мы не контролируем, существенно зависит результат f(u,) наших контро-лируемых действий u. Приведём для удобства читателей ещё раз обычно используемое обозначение для задачи оптимизации при неопределённости и риске: f(u,) → maxuQ, (1.1) Ещё раз напомним, что в этих условиях рационального партнёра ∕ противника нет, и, значит, нет никакой другой функции выигрыша, кроме исходной функции f(u,), которую желательно максимизировать. При этом нет почти никаких оснований предполагать хоть что-то о независящих от нас значениях . Известным можно считать лишь множество всех возможных значений этого фактора. Однако можно делать предположения об отно-шении единственного игрока ЛПР, выбирающего управление uQ, к неопределеннос-ти и риску. Различные предположения такого рода и определяемые ими решения и рас-смотрены в разделах настоящей главы. В 1-ом разделе вводятся необходимые для даль-нейшего формальные понятия и обозначения, самыми важными из которых являются пла-тежная матрица и матрица потерь. Во 2-ом разделе рассматриваются основные правила принятия решения (т.е. выбора управления uQ), отражающие представления и характер ЛПР. Наконец, 3-ий раздел посвящён задачам оптимизации при известных вероятност-ных характеристиках неконтролируемых факторов. Последние имеют специальное фор-мальное название – оптимизации в условиях риска, хотя про риск в содержательном смыс-ле говорится и при отсутствии каких бы то ни было вероятностных характеристик у не-контролируемых факторов. Примерами неопределенностей, для которых практически ничего нельзя сказать о бу-дущих «состояниях природы», могут служить: спрос и объемы продаж на действительно новую продукцию, которой ранее на рынке не было; состояние фондового рынка, рынка товаров и услуг, и вообще экономики в буду-щем (через месяц, год, несколько лет и т. д.); успех или неуспех новой книги, нового фильма, телепередачи и т. п.; возникновение природных, социальных и экономических катаклизмов; молодежные музыкальные течения, и вообще состояние культуры через несколько лет; любые творческие процессы в будущем, например в науке, литературе, кино, теат-ре и др.; спортивные результаты в предстоящих олимпийских играх, и множество других примеров, не говоря уже о том, что «нам не дано предугадать как наше слово отзо-вется». Однако и в условиях полной неопределенности, теория принятия решений помогает структурировать проблему и предоставить ЛПР достаточно обоснованные рекомендации. При принятии решений в условиях неопределенности выбор метода принятия наилучшего решения, также как и выбор окончательного решения, полностью зависят от вкусовых пристрастий и целей ЛПР, поэтому говорить об объективной оптимальности не приходит-ся. В главе использованы материалы из книг [1]. В ней можно найти дополнительные упражнения по данной теме. 1. 1. Формализация задачи. Платежная матрица и матрица потерь Обозначим множество всех возможных значений неконтролируемых факторов через G. Заметим, что элементами множества G могут быть любые формальные объекты, в том числе векторы, функции, таблицы, графы и пр. Множество возможных управлений выше уже было обозначено через Q; оно также может состоять из объектов любой природы, а не только из чисел. Гораздо важнее для нас будет предположение о том, что оба множества – G и Q – будут предполагаться конечными. Хотя почти все дальнейшие выводы справедливы и для бесконечных множеств, это предположение практически не ограничивает круг рассматриваемых ситуаций, в то же время значительно упрощая необ-ходимые формальные рассуждения. Следуя руководству [2], будем сопровождать изложение простым содержательным примером. Пример 1.1. Сезонный торговец прохладительными напитками продает напитки в сезон (в августе), а заказать их поставку от оптовика и оплатить заказ он должен уже в марте. Оптовик поставляет прохладительные напитки только малыми (1000 л), средними (2000 л) или крупными (3000 л) партиями. Торговец закупает напитки в марте по цене $ 1 за 1 л, продает их в августе по цене $ 1,5 за 1 л, а если к концу сезона (к сентябрю) у него остаются нераспроданные напитки, он возвращает их оптовику, но уже по цене $ 0,7 за 1 л. По своему прошлому опыту торговец знает, что объемы продаж прохладительных напитков зависят от состояния погоды в августе. Так, если в августе будет холодно, то объём продаж составит скорей всего 500 л, если прохладно – 900 л, если тепло – 2000 л и если жарко – 2800 л. Торговцу необходимо принять решение о том, какую партию прохладительных напит-ков ему следует заказать у оптовика в марте, чтобы получить наибольшую прибыль от их продажи в августе. Обсуждение. Торговец вынужден принимать решение об объёме закупаемой партии напитков в марте, ничего не зная о том, какая погода будет в действительности в августе, в сезон его продаж. От состояния погоды в августе зависит спрос на напитки и объемы продаж и, следовательно, объем закупаемых в марте напитков. Если торговец закупит в марте крупную партию напитков, а в августе будет холодно, то покупателей будет мало, объем продаж будет низким и он понесет убытки, если же будет закуплена малая партия, а в августе будет жарко, то он не сможет удовлетворить весь спрос и, следовательно, упус-тит свою выгоду. 1.1.1. Матрица платежей. Платежи представляют собой зависящие от решений про-давца (в марте) и погоды (в августе) прибыли или убытки (которые удобно считать отрицательными прибылями). Для построения матрицы платежей необходимо определить природу, перечислить все её состояния, выработать возможные решения продавца по объему закупаемой партии напитков, определить формулу для расчета платежей и вычис-лить их для всех сочетаний состояний природы и возможных решений. Природой является состояние погоды в августе. Поскольку между состояниями пого-ды и спросом на напитки существует тесная связь, то под природой можно понимать как состояние погоды, так и спрос на напитки. Торговец выделяет четыре состояния приро-ды – холодно (С1), прохладно (С2), тепло (С3) и жарко (С4), что соответствует четырем уровням спроса на напитки – низкий (500 л), средний (900 л), хороший (2000 л) и отличный (2800 л). Возможные решения А1, А2, А3, которые может принять торговец – это выбрать объём партии напитков, которые он может закупить у оптовика: 1000 л (А1), 2000 л (А2) или 3000 л (А3). Платежи торговца представляют собой возможные прибыли или убытки и вычисля-ются по формуле: Платеж = Прибыль = Доход от продажи в августе + Выручка от возврата нераспроданных напитков оптовику ‒ Затраты на покупку в марте. Матрица платежей строится с учетом конкретных условий последовательно для каж-дого возможного решения, начиная с первого и просматривая все состояния природы. При вычислениях прибыли необходимо понимать, что спрос ‒ это возможное количество напитков, которое может быть куплено потребителями, а объем продаж ‒ это минимум из двух величин: спроса и предложения. Если спрос в сезон больше предложения продавца (т. е. объема закупленной им партии напитков), то продавец реально сможет продать только то, что он имеет в наличии, упустив свою выгоду, если же предложение превышает спрос, то у продавца останется нереализованная часть напитков. Покажем, как вычисляется прибыль, если продавец примет решение А1 ‒ закупить партию напитков в размере 1000 л. В этом случае затраты составят $ 1 × 1000 л = $ 1000. Далее последовательно просматриваются все состояния природы, начиная с первого (см. перечень состояний природы выше). Если в августе будет холодно, предложение продавца (1000 л), равное объему закуп-ленной партии напитков, превысит спрос (500 л) на 500 л, поэтому у продавца останутся нераспроданными 500 л напитков, которые он будет вынужден вернуть оптовику по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 500 = $ 750, а выручка от возврата напитков $ 0,7 × 500 = $ 350. При рассматриваемом решении А1 расход на покупку в марте составляет $ 1000. В результате продавец получит прибыль: $ 750 + $ 350 ‒ $ 1000 = $ 100. Если в августе будет прохладно, предложение продавца (1000 л), равное объему за-купленной партии напитков, превысит спрос (900 л) на 100 л, поэтому у продавца останутся нераспроданными 100 л напитков, которые он будет вынужден вернуть оптови-ку по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам соста-вит $ 1,5 × 900 = $ 1350, а выручка от возврата напитков $ 0,7 × 100 = $ 70. При рассмат-риваемом решении А1 расход на покупку в марте составляет $ 1000. В результате про-давец получит прибыль: $ 1350 + $ 70 ‒ $ 1000 = $ 420. Если в августе будет тепло, предложение продавца (1000 л), равное объему закуплен-ной партии напитков, не покроет спрос (2000 л), поэтому у продавца не останется нерас-проданных напитков. Поэтому весь доход продавца составит выручка от продажи напитка клиентам $ 1,5 × 1000 = $ 1500. При рассматриваемом решении А1 расход на покупку в марте составляет $ 1000. В результате продавец получит прибыль: $ 1500 ‒ $ 1000 = $ 500. Наконец, если в августе будет жарко, предложение продавца (1000 л), равное объему закупленной партии напитков, не покроет спрос (2800 л), поэтому у продавца не останется нераспроданных напитков. Поэтому весь доход продавца составит выручка от продажи напитка клиентам $ 1,5 × 1000 = $ 1500. При рассматриваемом решении А1 расход на по-купку в марте составляет $ 1000. В результате продавец получит прибыль: $ 1500 ‒ $ 1000 = $ 500. Запишем найденные 4 числа: 100, 420, 500, 500 в верхнюю строку табл. 1.1, соответст-вующую решению А1 продавца. Аналогично подсчитаем платежи продавца, которые он может получить при различ-ных состояниях природы, если он примет решение А2 закупить партию напитка в 2000 л: Если в августе будет холодно, предложение продавца (2000 л), равное объему закуп-ленной партии напитков, превысит спрос (500 л) на 1500 л, поэтому у продавца останутся нераспроданными 1500 л напитков, которые он будет вынужден вернуть оптовику по бо-лее низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 500 = $ 750, а выручка от возврата напитков $ 0,7 × 1500 = $ 1050. При рассматриваемом решении А2 расход на покупку в марте составляет $ 2000. В результате продавец получит прибыль (точнее, убыток): $ 750 + $ 1050 ‒ $ 2000 = ‒$ 200. Если в августе будет прохладно, предложение продавца (2000 л), равное объему за-купленной партии напитков, превысит спрос (900 л) на 1100 л, поэтому у продавца оста-нутся нераспроданными 1100 л напитков, которые он будет вынужден вернуть оптовику по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 900 = $ 1350, а выручка от возврата напитков $ 0,7 × 1100 = $ 770. При рассматри-ваемом решении А2 расход на покупку в марте составляет $ 2000. В результате продавец получит прибыль: $ 1350 + $ 770 ‒ $ 2000 = $ 120. Если в августе будет тепло, предложение продавца (2000 л), равное объему закуплен-ной партии напитков, совпадёт со спросом (2000 л), поэтому у продавца не останется нераспроданных напитков. Поэтому весь доход продавца составит выручка от продажи напитка клиентам $ 1,5 × 2000 = $ 3000. При рассматриваемом решении А2 расход на покупку в марте составляет $ 2000. В результате продавец получит прибыль: $ 3000 ‒ $ 2000 = $ 1000. Наконец, если в августе будет жарко, предложение продавца (2000 л), равное объему закупленной партии напитков, не покроет спрос (2800 л), поэтому у продавца не останется нераспроданных напитков. Поэтому весь доход продавца составит выручка от продажи напитка клиентам $ 1,5 × 2000 = $ 3000. При рассматриваемом решении А2 расход на по-купку в марте составляет $ 2000. В результате продавец получит прибыль: $ 3000 ‒ $ 2000 = $ 1000. Запишем найденные 4 числа: ‒200, 120, 1000, 1000 во вторую строку табл. 1.1, соответствующую решению А2 продавца. Наконец, подсчитаем платежи продавца, которые он может получить при различных состояниях природы, если он примет решение А3 закупить партию напитка в 3000 л: Если в августе будет холодно, предложение продавца (3000 л), равное объему закуп-ленной партии напитков, превысит спрос (500 л) на 2500 л. Поэтому у продавца останутся нераспроданными 2500 л напитков, которые он будет вынужден вернуть оптовику по бо-лее низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 500 = $ 750, а выручка от возврата напитков $ 0,7 × 2500 = $ 1750. При рассматриваемом решении А3 расход на покупку в марте составляет $ 3000. В результате продавец получит прибыль (точнее, убыток): $ 750 + $ 1750 ‒ $ 3000 = ‒$ 500. Если в августе будет прохладно, предложение продавца (3000 л), равное объему за-купленной партии напитков, превысит спрос (900 л) на 2100 л, поэтому у продавца оста-нутся нераспроданными 2100 л напитков, которые он будет вынужден вернуть оптовику по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 900 = $ 1350, а выручка от возврата напитков $ 0,7 × 2100 = $ 1470. При рассматри-ваемом решении А3 расход на покупку в марте составляет $ 3000. В результате продавец получит прибыль (точнее, убыток): $ 1350 + $ 1470 ‒ $ 3000 = ‒$ 180. Если в августе будет тепло, предложение продавца (3000 л), равное объему закуплен-ной партии превысит спрос (2000 л), поэтому у продавца останутся нераспроданными 1000 л напитков, которые он будет вынужден вернуть оптовику по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 2000 = $ 3000, а вы-ручка от возврата напитков $ 0,7 × 1000 = $ 700. При рассматриваемом решении А3 расход на покупку в марте составляет $ 3000. В результате продавец получит прибыль: $ 3000 + $ 700 ‒ $ 3000 = $ 700. Наконец, если в августе будет жарко, предложение продавца (3000 л), равное объему закупленной партии напитков, покроет спрос (2800 л), поэтому у продавца останутся не-распроданными 200 л напитков, которые он будет вынужден вернуть оптовику по более низкой цене $ 0,7 за 1 л. Доход продавца от продажи напитка клиентам составит $ 1,5 × 2800 = $ 4200, а выручка от возврата напитков $ 0,7 × 200 = $ 140. При рассматриваемом решении А3 расход на покупку в марте составляет $ 3000. В результате продавец получит прибыль: $ 4200 +$ 140‒ $ 3000 = $ 1340. Запишем найденные 4 числа: ‒500, ‒180, 700, 1340 в третью строку табл. 1.1, соответ-ствующую решению А3 продавца. Таблица 1.1. Платежная матрица продавца прохладительных напитков
В клетки таблицы 1.1 записаны платежи (положительные или отрицательные), которые получает продавец в зависимости от своих решений и состояний природы. В общем случае аналогичная платёжная таблица составляется по задаче (2) с конечн-ым множеством Q альтернатив (решений ЛПР) и конечным множеством G состояний природы. Строки таблицы соответствуют решениям из Q, столбцы – состояниям природы из G. В клетку таблицы на пересечении i-ой строки и j-го столбца записывается платёж aij, получаемый ЛПР при выборе альтернативы ui, если неконтролируемое состояние приро-ды равно j. Платёжные матрицы будут представляться в следующем виде: Таблица 1.2. Общий вид платежной матрицы
Следует иметь в виду, что вычисление платежей в реальных ситуациях далеко не всег-да является столь же элементарной задачей, как в рассмотренном примере. Однако в рам-ках данного пособия мы будем предполагать, что все платежи aij из платёжной матрицы известны или хотя бы могут быть найдены без особых проблем. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
