Неопределенность на входе. Принятие решений при неопределённости и риске введение
 Скачать 165.09 Kb.
|
|
1.2.3. Критерий Лапласа. Поскольку нам неизвестно, каким будет состояние приро-ды, то есть смысл выбрать ту альтернативу, при которой сумма платежей по всем состоя-ниям природы будет максимальной. Применительно к задаче продавца напитков, платеж-ная матрица которого приведена в Табл. 1.1, имеем: при выборе альтернативы А1 сумма всех платежей равна $ 1520; при выборе альтернативы А2 сумма всех платежей равна $ 1920; при выборе альтернативы А3 сумма всех платежей равна $ 1360. Таким образом, в соответствии с критерием Лапласа выбирается альтернатива А2. В общем случае процедура применения критерия Лапласа очень проста: выбирается та альтернатива, для которой сумма элементов соответствующей строки платежной матрицы максимальна. 1.2.4. Максимаксный критерий. Этот критерий настолько же оптимистичен, насколько критерий Вальда пессимистичен. ЛПР, применяющий максимаксный критерий, склонен к риску и верит, что наступит такое состояние природы, при котором его выигрыш будет наибольшим. Для такого ЛПР выигрыш имеет большую значимость, чем проигрыш (выигрыш ‒ все, проигрыш ‒ ничто). Применительно к задаче продавца напитков, платежная матрица которого приведена в Табл. 1.1, имеем: при выборе альтернативы А1 максимальный платёж равен $ 500; при выборе альтернативы А2 максимальный платёж равен $ 1000; при выборе альтернативы А3 максимальный платёж равен $ 1340. Таким образом, в соответствии с максимаксным критерием выбирается альтернатива А3. В общем случае процедура применения максимаксного критерия очень проста: выби-рается та альтернатива, для которой максимальный элементв соответствующей строки платежной матрицы максимален. Главный вывод из материала данного раздела состоит в следующем. Разные правила принятия решений приводят к выбору разных альтернатив даже в очень простых ситуаци-ях. Наличие некоторых других правил, которые здесь не рассматриваются, никак не меня-ют данного, возможно, не слишком приятного, вывода. Это соответствует одному из давно и хорошо известных в околонаучной литературе законов О’Мёрфи: «Есть правила для принятия решений, но нет правила для выбора этих правил». 1.3. Принятие решений в условиях риска Задачи принятия решений в условиях риска характеризуются наличием нескольких альтернатив, нескольких состояний природы и, главное, тем, что состояния природы носят случайный характер, т.е. их можно рассматривать как случайные события. Сам случайный характер состояний природы является существенной характеристикой моделей принятия решений в условиях риска, так как далеко не всякую неопределенность можно трактовать как случайное явление. Перечень примеров, когда такое рассмотрение практически невоз-можно, приведён выше (непосредственно перед разделом 1.1). Случайная природа состоя-ний природы в условиях риска позволяет изучать их методами теории вероятностей и ма-тематической статистики (ТВМС) и оценивать значения вероятностей наступления тех или иных состояний. Здесь следует указать на достаточно распространённую ошибку, ког-да при анализе различных сложных систем явно – а чаще неявно – неопределённость трак-туется как случайность и, как следствие, методы ТВМС применяются безо всякого обос-нования. Один из примеров такой ошибки приведён в §15.3 учебника [1], при описании прихода танкеров на нефтяной терминал, когда этот процесс трактовался как случайный (простейший поток событий). Наличие принципиальной возможности определения вероятностей состояний приро-ды позволяет отнести модели принятия решений в условиях риска к моделям с неполной неопределенностью. В отличие от последних, в рассмотренных выше задачах принятия решений в условиях полной неопределенности состояния природы нельзя рассматривать как случайные события, даже располагая релевантным статистическим материалом. Так, будущий успех (или провал) нового спектакля, является полностью неопределенным и не-предсказуемым событием, несмотря на имеющуюся статистику по прошлым спектаклям в том же театре и у тех же режиссёров. Напомним два понятия ТВМС: полная группа наступления состояний природы и ожи-даемое значение случайной величины. Полная группа состояний природы. Состояния природы С1, С2, ..., Сn в моделях принятия решений в условиях риска являются случайными явлениями. Будем считать, что они образуют полную группу несовместных событий. Это означает, что какое-либо од-но состояние природы обязательно реализуется в действительности и, кроме того, никакие два состояния природы не могут появится одновременно. В этом случае вероятности нас-тупления состояний природы р1, р2, ..., рn должны удовлетворять равенству: р1 + р2 +...+ рn = 1. Пусть, например, нас интересует, будет ли дождь в следующее воскресенье. Приро-дой здесь является погода в интересующий нас день, и мы рассматриваем два состояния природы – С1 (дождь есть) и С2 (дождя нет). Поскольку хотя бы одно из событий – дождь есть, дождя нет, – обязательно наступит, и при этом наступит только одно из них, то состояния природы Cl и С2 образуют полную группу несовместных событий. Вероятность дождя p1 может быть оценена на основании многолетних наблюдений за погодой. Так, если за сто последних лет дождь в этот день наблюдался 30 раз, то вероятность дождя p1 будет равна 30 ∕ 100 = 0,3; при этом вероятность отсутствия дождя p2 будет равна 1 – p1 = 1 – 0,3 = 0,7. Ожидаемое значение случайной величины. Ожидаемое значение случайной вели-чины, называемое еще математическим ожиданием или просто средним значением слу-чайной величины, определяется следующим образом. Если некоторая случайная величина х может принимать одно из своих возможных значений x1, x2, ..., xn с соответствующими вероятностями р1, р2, ..., рn, то ожидаемое значение  случайной величины х определяется как сумма произведений всех её возможных значений на их вероятности, т. е. = р1x1+ р2x2 +...+ рnxn.Можно сказать, что ожидаемое значение случайной величины является взвешенным средним всех возможных значений случайной величины с весами, равными вероятностям этих значений. В моделях принятия решений в условиях риска для выбора наилучшего решения используются два критерия (или метода, основанного на критериях): критерий максимального ожидаемого платежа (выигрыша), критерий минимальной ожидаемой потери. 1.3.1. Критерий максимального ожидаемого платежа. Принятие решений по крите-рию максимального ожидаемого платежа основывается на представлении операции в виде платежной матрицы, а выбор наилучшего решения осуществляется по максимальному значению ожидаемого платежа среди ожидаемых платежей для всех возможных решений. Построим платежную матрицу для принятия решений в условиях риска (Табл. 1.5). В ней представлены альтернативы A1, А2, ..., Аm, состояния природы С1, С2, ..., Сn и вероятнос-ти их наступления р1, р2, ..., рn. Каждому возможному состоянию природы и каждому принятому решению соответствует значение платежа. Поскольку состояния природы являются случайными событиями, то платежи для каждого принятого решения можно трак-товать как возможные значения случайной величины платежа, которые реализуются при наступлении данного состояния природы. Другими словами, если принято i-ое решение Аi, то возможные значения платежей аi1, аi2, ..., ain при различных состояниях природы являются реализациями случайной величины платежа, принимающей свои значения аi1, аi2, ..., ain с вероятностями р1, р2, ..., рn. 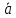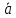В соответствии с этим, значение ожидаемого платежа  iдля принятого решения Аi вычисляется как i= р1аi1+ р2аi2 +...+ рnain (i = 1, …, m). (1.4)Выбор наилучшего решения в условиях риска основывается на выборе максимального значения ожидаемого платежа, вычисленного для всех возможных решений. Другими сло-вами, решение будет оптимальным, если оно соответствует максимальной величине ожи-даемого платежа  .среди ожидаемых платежей. Вернёмся к задаче торговца прохладительными напитками, представленной в пункте 1.1.1 платёжной матрицей из Табл. 1.1. В отличие от рассмотренной ранее ситуации, здесь предполагается, что известны вероятности р1 = 0,1; р2 = 0,2; р3 = 0,4; р4 = 0,3 холодной, прохладной, тёплой и жаркой погоды в августе. Для принятия наилучшего решения торговец вычисляет ожидаемые платежи для каждого возможного решения: для решения А1 (закупить 1000 л) 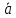1= 100•0,1 + 420•0,2 + 500•0,4 + 500•0,3 = 444;для решения А2 (закупить 2000 л) 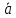2 = (‒200)•0,1 + 120•0,2 + 1000•0,4 + 1000•0,3 = 704; для решения А3 (закупить 3000 л) 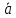3 = (‒500)•0,1 + (‒180)•0,2 + 700•0,4 + 1340•0,3 = 596. Среди найденных значений выбирается максимальное значение 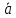2=704. Оно соответству-ет решению А2. Таким образом, согласно критерию максимального ожидаемого платежа оптимальным для торговца решением будет решение закупить у оптовика 2000 л прох-ладительных напитков. Все данные, включая посчитанные ожидаемые платежи, представлены в Табл. 1.5. Таблица 1.5. Платежная матрица торговца прохладительными напитками для принятия наилучшего решения по критерию максимального ожидаемого платежа
1.3.2. Критерий минимальных ожидаемых потерь. Данный метод принятия наилучшего решения основывается на матрице потерь и величине ожидаемых потерь, вычисляемых для каждого решения. Как и величины платежей, значения потерь для каждого возможного решения можно трактовать как отдельные реализации случайной величины потерь при наступлении различных состояний природы. Поэтому можно говорить об ожидаемой величине потерь, которая для каждого возможного решения Аi (i = 1,2, ..., т)рассчитывается по формуле:  i= р1ri1+ р2ri2 +...+ рnrin (i = 1, …, m). (1.5)Оптимальное решение соответствует минимальному значению ожидаемых потерь, выбранному из ожидаемых потерь i, вычисленных для всех возможных решений, т. е. минимальной величине ожидаемых потерь min1 ≤ i≤ m i.Вернёмся ещё раз к задаче торговца прохладительными напитками, представленной в пункте 1.1.2 матрицей из Табл. 1.3. Вероятности состояний природы р1 = 0,1; р2 = 0,2; р3 = 0,4; р4 = 0,3 холодной, прохладной, тёплой и жаркой погоды в августе те же самые, что в предыдущем пункте 1.3.1. Для принятия наилучшего решения торговец вычисляет ожидаемые потери для каждого возможного решения: для решения А1 (закупить 1000 л) 1= 0•0,1 + 0•0,2 + 500•0,4 + 840•0,3 = 452;для решения А2 (закупить 2000 л) 2 = (300)•0,1 + 300•0,2 + 0•0,4 + 340•0,3 = 192; для решения А3 (закупить 3000 л) 3 = (600)•0,1 + (600)•0,2 + 300•0,4 + 0•0,3 = 300.Среди найденных значений выбирается минимальное значение 2 = 192. Оно соответствуетрешению А2. Таким образом, согласно критерию минимальных ожидаемых потерь опти-мальным для торговца решением будет решение закупить у оптовика 2000 л прохлади-тельных напитков. Все данные, включая посчитанные ожидаемые потери, представлены в Табл. 1.6. Таблица 1.6. Матрица торговца прохладительными напитками для принятия наилучшего решения по критерию минимальных ожидаемых потерь
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||