Конспект лекций для студентов специальности 050716 Приборостроение вскемен УстьКаменогорск 2008 содержание X, 7
 Скачать 282.51 Kb. Скачать 282.51 Kb.
|
     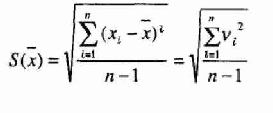   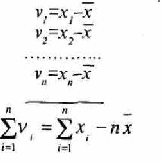   Министерство образования и науки Республики Казахстан Министерство образования и науки Республики КазахстанВОСТОЧНО-КАЗАХСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Д. Серикбаева Л.А. Проходова ОСНОВЫ ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫХ ТЕХНОЛОГИЙ Конспект лекций для студентов специальности 050716 Приборостроение вскемен Усть-Каменогорск 2008 СОДЕРЖАНИЕ X, 7 У oJb ' 12 Жх)=(х1-а?Р1+(хг-а)2Рг+...+(х„-а)2Р„='£8!Р,=о2, 14 ул 14 ВВЕДЕНИЕ Правильное и эффективное ведение технологических процессов немыс лимо без контроля за целым рядом технологических параметров, характери зующих процесс. Контроль тесно связан с измерением технологических пара метров, осуществляемым с помощью специальных технических средств. Сово купность технических средств, служащих для выполнения измерений, методов и приемов проведения измерений и интерпретации их результатов, принято оп ределять понятием измерительная техника. В промышленности измерительная техника является неотъемлемой частью технологических процессов, так как ис пользуется для получения информации о многочисленных режимных парамет рах, определяющих ход процесса. Область измерительной техники, объеди няющую измерительные устройства и методы измерений, используемые в тех нологических процессах, принято определять понятием технологические изме рения. Набор измеряемых параметров, включаемых в технологические измере ния, весьма различен для разных отраслей промышленности и во многом зави сит от специфики технологических процессов. Измерения давления, температу ры, расхода и уровня принято называть теплотехническими измерениями; из мерения состава и физико-химических свойств вещества - физико-химическими измерениями, а измерения электрических величин - электрическими измере ниями.
Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств. Для проведения измерения необходимо наличие:
Цель измерения - получение значения физической величины в форме, наиболее удобной для пользования. Что понимают под физической величиной, значение которой находят опытным путем? Физическая величина, как уже отмечалось выше, - это характеристика физического объекта (физической системы, явления или процесса), общая в ка чественном отношении для многих физизических объектов, но в количествен ном отношении индивидуальная для каждого из них. Индивидуальность понимается в том смысле, что свойство может для од ного объекта в определенное число раз быть больше или меньше, чем для дру гого объекта. Примерами физических величин могут служить плотность, тем пература плавления, показатель преломления света и многие другие. Физическая величина характеризуется размером, значением, числовым значением, истинным и действительным значениями. Размер физической величины - количественная определенность физиче ской величины, присущая конкретному материальному объекту, системе, явле нию или процессу. Значение физической величины - выражение размера физической вели чины в виде некоторого числа принятых для нее единиц. Числовое значение физической величины - отвлеченное число, входящее в значение величины. «Величина» - многовидовое понятие. Но термином «величина» часто вы ражают размер конкретной физической величины. Неправильно говорить «ве личина скорости», «величина напряжения», так как и скорость, и напряжение являются величинами. Между размером и значением величины есть разница. Размер величины существует реально. Выразить размер величины можно любой из единиц дан ной величины при помощи числового значения. Числовое значение изменяется в зависимости от выбранных единиц, тогда как физический размер величины остается- неизменным. Единица физической величины - физическая величина фиксированного размера, которой условно присвоено числовое значение, равное 1. Физическую величину характеризует ее истинное значение, которое идеальным образом отражает в качественном и количественном отношении со ответствующее свойство объекта. Действительным называют значение физической величины, найденное экспериментальным путем и настолько приближенное к истинному значению, что для данной цели может быть использовано вместо него.
По способу получения числового значения измеряемой величины все измерения делятся на четыре основных вида: прямые, косвенные, совокупные и совместные. Прямыми называются измерения, при которых искомое значение физи ческой величины получают непосредственно из опытных данных (например, измерение массы на весах, длины детали микрометром). Строго говоря, измерение всегда прямое и рассматривается как сравнение величины с ее единицей. В этом случае лучше применять термин «прямой ме тод измерения». Косвенные измерения- определение искомого значения физической ве личины на основании результатов прямых измерений других физических вели чин, функционально связанных с искомой величиной. Косвенные измерения проводятся в тех случаях, когда:
Уравнение косвенных измерений: у = f (х1, х2,... хп), где у - искомая вели чина, являющаяся функцией аргументов х1, х2,..., хп, полученных прямыми из мерениями. Примером косвенных измерений является определение твердости (НВ) металлов путем вдавливания стального шарика определенного диаметра (D) с определенной нагрузкой (Р) и получения при этом определенной глубины от печатка (h): НВ = Р /(П) Совокупными называются проводимые одновременно измерения не скольких одноименных величин, при которых значения искомых величин нахо дят решением системы уравнений, получаемых при прямых измерениях. Например измерения, при которых массы отдельных гирь набора находят по известной массе одной из них и по результатам прямых сравнений масс раз личных сочетаний гирь. Совместные измерения - это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения функциональ ной зависимости между ними. Например, определения зависимости длины тела от температуры, температур кипения и плавления от давления и т.д. Измерения могут быть классифицированы: а) по характеристике точности - равноточные (ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерения и в одних и тех же условиях) и неравноточные (ряд измерений какой-либо вели чины, выполненных несколькими различными по точности средствами измере ния и (или) в нескольких разных условиях); б) по числу измерений в ряду измерений - однократные и многократ ные; в) по отношению к изменению измеряемой величины - статические (из мерение неизмененной во времени физической величины, например, измерение длины детали при нормальной температуре или измерение размеров земельного участка) и динамические (измерение изменяющейся по размеру физической величины, например, измерение переменного напряжения электрического тока, измерение расстояния до уровня земли со снижающегося самолета); г) по выражению результата измерения - абсолютные (измерение, осно ванное на прямых измерениях величин и (или) использовании значений физи ческих констант, например, измерение силы F основано на измерении основной величины массы m и использовании физической постоянной - ускорения сво бодного падения g) и относительные (измерение отношения величины к од ноименной величине, выполняющей роль единицы). Измерить состав или свойство веществ или измерить физическую вели чину можно, используя тот или иной метод измерения. Метод измерения - это прием или совокупность приемов сравнения изме ряемого состава или свойства вещества или измеряемой физической величины с известным составом или свойством вещества или с единицей физической ве личины в соответствии с реализованным принципом измерений. Принцип измерений - это явление или эффект, положенные в основу из мерений. Рассмотрим некоторые принципы, которые положены в основу измере ний. Если нагревать места спая двух электродов из разнообразных материалов, то возникает ЭДС. Указанное явление положено в основу измерения темпера туры с высокой точностью (термопары). При нагревании электрических проводников и полупроводников изменя ется их сопротивление. Это явление позволяет получать высокую точность из мерения температуры, особенно с применением платины. Применение полу проводников дает возможность измерять малые интервалы температур и тем пературу тел, имеющих очень малые объемы. При растяжении или сжатии некоторых материалов изменяется их элек трическое сопротивление, что положено в основу измерения малых деформа ций тел, а также высокого и сверхвысокого давлений. На границе металла и полупроводника при освещении возникает ЭДС, так называемый фотоэлектрический эффект. На использовании фотоэффекта основаны фотоэлементы, которые применяются во многих средствах измере ний. Яркость свечения тела зависит от температуры, которая, в свою очередь, зависит от силы тока, накаливающего тело. На этом явлении основан бескон тактный метод измерения температуры (оптический пирометр). Каждую величину можно измерить различными методами.
По общим приемам получения результатов измерений различают: 1) пря ной метод измерений; 2) косвенный метод измерений. Первый метод реали зуется при прямом измерении, второй - при косвенном измерении, которые описаны выше. По условиям измерения различают: 1) контактный и 2) бесконтактный методы измерений. Контактный метод измерений основан на том, что чувствительный элемент средства измерений приводится в контакт с объектом измерения (из мерение температуры тела термометром). Бесконтактный метод измерений основан на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения (измерение расстояния до объекта радиолокатором, измерение температуры в доменной печи пирометром). Исходя из способа сравнения измеряемой величины с ее единицей, разли чают: 1) метод непосредственной оценки и 2) метод сравнения с мерой. Метод непосредственной оценки - метод, при котором значение вели чины определяют непосредственно по показанию средства измерений (термо метра, вольтметра). Этот метод обеспечивает быстроту процесса измерений, но точность измерения ограничена. В случае выполнения особо точных измерений применяется метод срав нения с мерой, в котором измеряемую величину сравнивают с величиной, вос производимой мерой. Например, измерение напряжения постоянного тока с помощью компенсатора сравнения с ЭДС нормального элемента. К разновидностям метода сравнения с мерой относят метод противопос тавления, дифференциальный (разностный) метод, нулевой метод, метод совпа дений и метод замещения. Метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами, называется методом противопоставления. Этим методом взвешивают груз на равноплечих весах, уравновешивая его гирями. Дифференциальный (разностный) метод характеризуется измерением разности между значениями измеряемой величины и величины, воспроизводи мой мерой. Например, измерения путем сравнения мер длины с эталонной ме рой на компараторе. Дифференциальный метод позволяет получать результаты с высокой точ ностью даже при применении средств измерений с невысокой точностью, но при условии воспроизведения известной величины с большой точностью.
на простом примере. Необходимо произвести измерение длины X с использованием меры дли ной L. Мера воспроизводит длину L с высокой точностью. Измерение Х1 определяется как Х1 ± А, где А - абсолютная погрешность, обеспечиваемая погрешностью в основном применяемого средства измерений. X=L + (Xt±A) = (L + XiUl±—^—), Lt Л | где - это относительная погрешность измерения длины X. Так как L значительно больше X1, то относительная погрешность измере ния X значительно меньше относительной погрешности измерения Хь L+X, Я, Например, измеряется длина X = 505 мм, мера L = 500 мм, Xi = 5 мм. Относительная погрешность измерения Xi равна — = 0,05 (1%), X, Д - 0,05 = 0,0001 (0,01%). 505 Следовательно, для достижения высокой точности можно воспользовать ся дифференциальным методом, применяя для измерения разности между из меряемой величиной и величиной, воспроизводимой мерой, более грубый при бор, что не внесет значительной погрешности, как показано на приведенном примере. Это дешевле, чем изготавливать средство измерений высокой точно сти для измерения всей величины в целом. Нулевой метод - метод сравнения с мерой, при котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Примером нулевого метода является взвешивание грузов на рычажных весах, измерение электрического сопротивления мостом с полным его уравно вешиванием. Если при дифференциальном методе необходимо иметь меру, значение которой близко к значению измеряемой величины, то преимущество нулевого метода в том, что можно применять меры во много раз меньше измеряемой ве личины. Например, в рычажных весах гирей в 1 кг можно уравновешивать мас сы взвешиваемых грузов в 100, 1000 и более килограммов. Метод совпадений - метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют по сов падению отметок шкал или периодических сигналов. Принцип совпадений заложен в основу построения нониуса штангенцир куля. Метод совпадений применяется при приеме сигналов времени, при ис пользовании биения, интерференции, стробоскопического эффекта. Метод замещения - это метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой (метод взве шивания на одном плече). Измерения - это процесс, завершающим этапом которого является «ре зультат измерения». За результатом измерений обязательно следуют действия. Можно выделить следующие основные функции измерений:
Перед измерениями ставится какая-то задача, цель и полученные резуль таты обязывают или к действиям, или к бездействию. Если результаты измере ний показывают соответствие выпускаемой продукции требованиям норматив ных документов, то продолжается выпуск продукции без каких-либо корректи рующих действий. В одних случаях результат измерений имеет небольшое значение, в дру гих от результата измерений могут зависеть открытие в науке, жизнь человека и т.д. Диапазон значимости целей, ради которых проводятся измерения, опре деляет диапазон требований, предъявляемых к результатам измерений и каче ству этих результатов. Основой любой формы управления (анализа, прогнозирования, планиро вания, контроля, регулирования) предприятием или отраслью является досто верная информация о количестве и качестве сырья, полуфабрикатов, готовой продукции, о ходе каждой технологической операции и всего производственно го цикла. Информация основывается на полученных результатах измерений. Информация будет достоверной, если она использует достоверные результаты измерений.
Основными характеристиками качества результата измерения являются:
Точность - это качество измерений, отражающее близость их результа тов к истинному значению измеряемой величины. Высокая точность измерений характеризуется малыми систематическими и случайными погрешностями. Точность оценивается обратной величиной модуля относительной погрешно сти. 3 3 Если погрешность измерения 10 , то его точность будет равна 10 . Пути повышения точности очень сложны, дорогостоящи, трудоемки. Но зачастую высокая точность нецелесообразна. В каждом конкретном случае не обходимо разбираться в требуемой точности измерений. Достоверность результата измерений - это степень доверия к резуль тату измерений. Как бы тщательно ни проводились измерения, какие бы высо коточные средства и методы ни использовались, никогда нельзя узнать истин ного значения измеряемой величины. При проведении повторных измерений одной и той же величины мы получаем, как правило, различные результаты. Каждый результат содержит какую-то погрешность Aj. = С! • С, где Ai. - погрешность i-ro результата измерений; Q - i-ый результат измерений; С - ис тинное значение измеряемой величины. Истинное значение неизвестно, следовательно, и Ai. неизвестна. Теория вероятности дала метод оценки степени приближения результата измерений к истинному значению измеряемой величины и научила оценивать вероятные границы погрешностей, за пределы которых они не выходят. Оценка дается с меньшей, чем 100%, достоверностью. Под правильностью измерений понимается качество измерений, отра жающее близость к нулю систематической составляющей погрешности измере ний. Сходимость - это качество измерений, отражающее близость друг к дру гу результатов измерений, полученных в одинаковых условиях. Сходимость характеризуется случайной составляющей погрешности результата измерений. Воспроизводимость - это такое качество измерений, которое отражает близость друг к другу результатов измерений, полученных в различных усло виях (разными методами и средствами измерений, в разных местах, в разное время).
Погрешность измерения - это отклонение результата измерения от ис тинного (действительного) значения измеряемой величины. Погрешность измерений представляет собой сумму целого ряда состав ляющих погрешностей, каждая из которых имеет свою причину. Погрешности результата измерения физической величины дают представление о том, какие цифры в его числовом значении являются сомнительными. Поэтому нет смысла выражать результат измерения большим числом цифр. Округлять числовое значение результата измерения следует в соответст вии с числовым разрядом значащих цифр погрешности, т.е. числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и зна чение погрешности. Лишние цифры в целых числах заменяются нулями, а в десятичных дро бях отбрасываются. Если десятичная дробь в числовом значении результата из мерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности. Погрешность результата измерений от неправильной установки средств измерений возникает у тех средств измерений, принцип действия кото рых связан с механическим равновесием, применением маятников, со строгим направлением вертикальной составляющей действующих сил и т.д. Внешние воздействия искажают результаты измерений. Например, при точных измерениях часто воспроизводят постоянные точки температурной шкалы (кипения, плавления, затвердевания), которые находятся в большой за висимости от атмосферного давления. Магнитное поле может влиять на пока зания любого средства измерений, имеющего подвижные части из магнитного материала. Заметное действие электромагнитное поле оказывает на показание средств измерений в области высоких частот. Влажность окружающего воздуха может быть причиной появления дополнительной погрешности в связи с гигро скопичностью материалов, которые изменяют свои геометрические размеры, электрическое сопротивление и другие свойства. Погрешности метода измерений - это теоретические погрешности, при чиной которых являются те или иные допущения и упрощения. Выявить источники и исключить методические погрешности - главное в технике эксперимента. Например, определить плотность р материала цилиндра можно по резуль татам измерения его геометрических размеров и массы т: m Р = D2 Т п L 4 В знаменателе - объем идеального цилиндра. В действительности же диа метр сечения цилиндра не является идеальной окружностью и по длине L име ется нарушение формы. «Неидеальность» формы и выбор величины, прини маемой за диаметр цилиндра, являются первым источником методической по грешности. Вторым источником погрешности являются непараллельность тор цов цилиндра и выбор величины, принимаемой за его длину. Третий источник погрешности - это округление числового коэффициента п. И наконец, четвер тым источником погрешности является масса как идеального по сплошности материала цилиндра, а в действительности внутри образца могут быть пустоты, пузырьки воздуха, попавшие при отливке. Субъективные погрешности являются следствием индивидуальных осо бенностей каждого человека:
По характеру проявления систематические погрешности подразделяются на постоянные, не изменяющие в течение всего времени ни значение, ни знак, и переменные, изменяющие в течение времени значение и (или) знак. Переменные погрешности могут быть:
К способам исключения систематических погрешностей измерений отно сятся (рисунок 11):
Случайная погрешность - составляющая погрешности измерений, изме няющаяся случайным образом при повторных измерениях одной и той же ве личины.
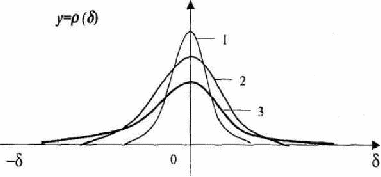
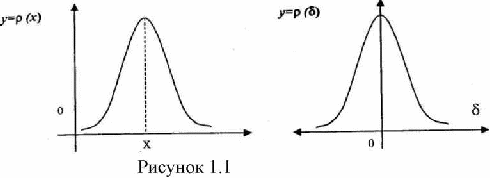
Случайные погрешности обусловливаются как случайным характером проявления физических процессов, происходящих в работающем приборе (тре ние, шум), так и случайными изменениями условий измерений, учет которых практически невозможен. В отличие от систематических погрешностей случайные погрешности нельзя исключить из результатов измерений путем введения поправок, даже ес ли известны причины и источники, их вызывающие. Однако их влияние на ре зультаты измерений может быть уменьшено увеличением числа измерений. Основной характеристикой любого случайного события, величины явля ется вероятность их появления, которая определяется как отношение числа случаев, благоприятствующих появлению данного события (значения величи ны), к общему числу всех возможных случаев, т.е. вероятность Р(А) какого-то случайного события А будет равна: Р( A) = —, N где nA - число случаев, благоприятствующих событию А; N - число всех возможных случаев. Если все N случаев благоприятствуют появлению события А, т.е. nA = N, то такое событие считается достоверным и его вероятность равна 1. Если же во всех N случаях нет ни одного, который бы благоприятствовал появлению собы тия А, т.е. nA = 0, то такое событие считается невозможным и его вероятность равна 0. Случайные величины и их вероятности изучают статистическим методом, проводя для этой цели большое число наблюдений. Для большого числа встре чающихся на практике случайных величин можно ожидать распределение по функции нормального распределения (закон Г аусса). Плотность нормального распределения для любой случайной величины описывается уравнением: у = ——е г°2 У oJb ' где у = р (х) - плотность вероятности (функции х); х - значение случайной величины, для которой определяется у; е=2,7183 - основание натурального логарифма; а = М(х) и о - параметры нормального распределения; М (х) - математическое ожидание случайной величины; о - среднее квадратическое отклонение. Если на оси абсцисс отложить результаты наблюдений над некоторой вели чиной, содержащей случайные погрешности, а по оси ординат - плотности веро ятности их появления, то получим график нормального распределения: Если систематические погрешности полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию результатов наблюдений. Абсцисса, соответствующая математическому ожиданию, называ ется центром распределения. Если по оси абсцисс откладывать разность полученного и истинного значения (х-а), то у=р(5) можно рассматривать как кривую распределения слу чайных погрешностей. Случайные погрешности измерений чаще всего распределяются нормально. Из графика на рисунке 1.1 видно, что наибольшая плотность вероятности соответствует погрешности 5 = 0. При возрастании погрешности как в сторону положительных, так и в сторону отрицательных значений (±5) вероятность уменьшается, т.е. чем больше погрешность 5, тем меньше плотность вероятно сти ее появления (тем реже можно ожидать ее появление). Снижение кривой и приближение ее к оси абсцисс означает, что плотность вероятности появления очень больших погрешностей чрезвычайно мала. Из гра фика видно (он симметричен относительно оси у), что погрешности, одинаковые по значению, но противоположные по знаку, имеют одинаковую плотность веро ятности. Математическое ожидание случайной величины - это такое ее значе ние, вокруг которого группируются результаты отдельных наблюдений. Матема тическое ожидание дискретной (прерывистой) случайной величины М(х) опреде ляется как сумма произведений всех возможных значений случайной величины на вероятность этих значений М (х) = £ х{ р! Для непрерывных случайных величин прибегают к интегрированию, для чего необходимо знать зависимость плотности вероятности от х, т.е. р(х), тогда: М{х) J xp{x)dx -■« Это означает, что математическое ожидание равно сумме бесконечно боль шого числа произведений всех возможных значений случайных величин х на бесконечно малые площади p(x)dx, где р(х) -ординаты для каждого х; dx - эле ментарные отрезки оси абсцисс. Если построить кривые нормального распределения случайных погрешно стей, то они могут иметь различный вид, как представлено в приведенном ниже графике. Рисунок 1.2 Площадь, расположенная под кривой распределения, для любой кривой со ответствует единице, поскольку кривая охватывает все значения случайной вели чины, т.е. все результаты наблюдений, а сумма вероятностей появления любого из возможных результатов равна единице. Из всего этого следует, что если при измере нии будет получен какой-то результат, то он будет достоверным. Для кривой 1 вся площадь сосредоточена вблизи у. Это означает, что большинство результатов мало отличается от математического ожидания, т.е. от нуля. В этом случае разброс результатов наблюдений (рассеяние) невелико и су ществует большая вероятность появления значений, близких к математическому ожиданию. Распределение по кривой 2 характеризуется значительным рассеянием. Вероятность появления больших погрешностей увеличилась, но и уменьшилась вероятность появления погрешностей, близких к нулю. Рассеяние по кривой 3 еще больше; заметно выше вероятность появления больших погрешностей. Мерой рассеяния значений случайной величины служит дисперсия Д (х), равная о2. Для дискретных распределений Жх)=(х1-а?Р1+(хг-а)2Рг+...+(х„-а)2Р„='£8!Р,=о2, f=) для непрерывных распределении ДМ - _[(*; - a)1 p{x)dx - о2.
Проведя ряд наблюдений, получаем числовые значения измеряемой вели чины. Вычислим среднее арифметическое значение: П ул
У _ 1 г «. _ 1=1 " " (1) где n - число наблюдений; _ х - среднее значение; хг результат i-го наблюдения. Результаты наблюдений свободны от систематической погрешности. Если расписать каждый результат наблюдений как истинное значение плюс погрешность и применить теорию вероятности, получим следующее вы ражение: | ||||||||||
