цйу. Документ Microsoft Word (2). Программа дисциплины Статистика
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
|
Пример 3. Рассчитаем среднее линейное отклонение по данным о производительности труда работников одной смены по данным таблицы 29. Таблица 29. Производительность труда работников I смены бригады рабочих на предприятии
Для нахождения средней арифметической вначале были рассчитаны середины каждого интервала и записаны в графу 3. Эти значения показывают, сколько в среднем деталей обрабатывает за смену один работник по каждой группе производительности труда. Данные значения мы обозначаем как Хi и будем использовать для дальнейших расчетов. Средняя производительность труда одного рабочего данной смены составляет 235 : 5 = 47 деталей: Индивидуальные отклонения от средней (без учета знака) указаны в графе 5. Взвешенные отклонения – в графе 6, их сумма составляет 20 единиц. Следовательно: 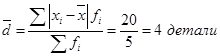 . .Это значит, что в среднем каждый работник данной смены обрабатывает за рабочее время на 4 детали меньше или больше, чем средний уровень производительности по смене, составляющий 47 деталей. Несмотря на то, что среднее линейное отклонение учитывает колеблемость всех значений признака, при его расчете в некотором смысле нарушается элементарное правило математики, так как отклонения от среднего значения суммируются без учета знаков. Избежать указанного недочета позволяет возведение каждого индивидуального отклонения от средней в квадрат. Рассчитав среднюю величину из возведенных в квадрат отклонений, можно вернуться к исходному порядку данных путем извлечения квадратного корня. Найденное число будет также характеризовать типичное отклонение вариантов признака от средней величины в данной совокупности. На практике квадратические оценки признаются более состоятельными, поскольку они не нарушают математических правил, а размер погрешности от возведения в квадрат является минимальным. Это объясняется вторым свойством средней арифметической величины (см. тему 5), согласно которому сумма квадратов отклонений от средней всегда меньше, чем аналогичная величина, рассчитанная от любого другого числа. Основными показателями вариации, для расчета которых используются квадратические оценки, являются дисперсия и среднее квадратическое отклонение. Дисперсия – это средняя арифметическая из квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается . В зависимости от исходных данных дисперсия может вычисляться как средняя арифметическая простая или взвешенная. Если каждый вариант признака повторяется только один раз, используют простую (невзвешенную) формулу: 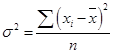 (36) (36)Если варианты признака повторяются неодинаковое количество раз, используют взвешенную формулу: 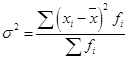 (37) (37)Среднее квадратическое отклонение (в литературе также часто используется термин «стандартное отклонение») представляет собой квадратный корень из дисперсии и обозначается . Формулы для его расчета следующие: · среднее квадратическое отклонение невзвешенное: 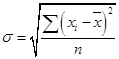 (38) (38)· среднее квадратическое отклонение взвешенное: 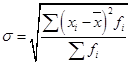 (39) (39)Математические преобразования формул (38) и (39) приводят к упрощенному виду формулы, которая часто оказывается более удобной на практике, особенно при расчете sпо несгруппированным данным: где 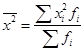 (41) (41)Среднее квадратическое отклонение является обобщающей характеристикой абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и показывает, насколько в среднем отличается значение каждого варианта признака от среднего значения для данной совокупности. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется соотношение: Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность. Для вычисления среднего квадратического отклонения необходимо рассчитать дисперсию. Порядок расчета дисперсии по взвешенной формуле: 1) определяют среднюю арифметическую взвешенную; 2) рассчитывают отклонения вариантов от средней: ; 3) возводят в квадрат отклонение каждого варианта от средней: 4) умножают квадраты отклонений на веса (частоты): 5) суммируют полученные произведения: 6) полученную сумму делят на сумму весов: 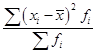 . .Пример 4. Найдем дисперсию и среднее квадратическое отклонение по данным о размере квартальной премии сотрудников одного из отдела фирмы (табл. 30). Таблица 30. Размер квартальной премии сотрудников отдела обслуживания фирмы
Исчислим среднюю арифметическую взвешенную: 500 : 50 = 10 тыс. руб. Значения отклонений от средней и их квадратов представлены в таблице 30 в графах 4 и 5. Определим дисперсию: 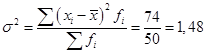 . .Среднее квадратическое отклонение будет равно: 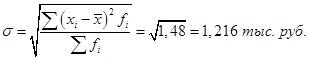 Это значит, что размер премии каждого сотрудника отдела обслуживания отличается от среднеквартальной величины премии по отделу, равной 10 тыс. руб., на 1 216 руб. Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить средины каждого интервала, и далее рассчитывать показатели вариации аналогичным образом. Пример 5. Рассчитаем дисперсию и среднее квадратическое отклонение по данным о распределении ценных бумаг по уровню доходности (табл. 31). Таблица 31. Распределение ценных бумаг по уровню доходности, %
Средняя доходность одной ценной бумаги равна: 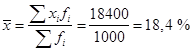 Исчислим дисперсию: 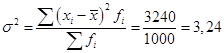 . .Среднее квадратическое отклонение составит: Следовательно, с каждой ценной бумаги владелец может получить в среднем на 1,8 % больше или меньше, чем величина средней доходности – 18,4 %. Для характеристики меры вариации изучаемого признака исчисляются показатели в относительных величинах. Они позволяют сравнивать характер вариации признака в разных совокупностях. Относительные показатели вариации рассчитывают как отношение типичного отклонения к средней величине, умножаемое на 100 %. Линейный коэффициент вариации характеризует долю среднего линейного отклонения от общего размера средней величины и рассчитывается по формуле: Коэффициент вариации рассчитывается как отношение среднего квадратического отклонения к средней величине: Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем, используемым для оценки типичности средних величин. Если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33,3 %. Пример 6. По данным таблицы 31 рассчитаем коэффициент вариации. Это означает, что ценные бумаги однородны по проценту доходности (т.к. V = 9,78 % < 33 %). Следует отметить, что коэффициент вариации может быть более 100 %, что бывает при наличии значений, сильно отличающихся от средней величины, например, отрицательных значений или аномально больших или малых значений отдельных вариантов. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине и для более качественного ее исследования необходимо разбить ее на более однородные части или с помощью специальных методов исключить влияние на среднюю аномальных вариантов. Вопрос 3. Математические свойства показателей вариации. На практике часто возникают ситуации, которые системно оказывают влияние на все значения исследуемого признака. Например, при системном сокращении или повышении расценок, переходе к использованию для расчетов условных единиц, переходе с одной валюты на другую (с доллара США к евро или фунтам стерлингов), при изменении шкалы измерений. Такие изменения отражаются в систематическом увеличении или уменьшении каждого значения показателя на некоторые фиксированные величины или в несколько раз. При таких изменениях необходимости в перерасчете всех показателей вариации не возникает, так как они обладают рядом математических свойств, зная которые, можно легко определить их величину по совокупности обновленных данных. Рассмотрим основные свойства на примере данных о затратах на производство единицы продукции трех отделений корпорации, каждое из которых в среднем ежемесячно производит 2 тыс. единиц продукции (табл. 32). Таблица 32. Затраты на производство единицы продукции по корпорации
Так как каждое отделение производит одинаковое количество продукции, для расчета обобщающих показателей – средней, дисперсии, среднего квадратического отклонения – можно воспользоваться невзвешенной формулой. Промежуточные расчеты показателей представлены в таблице 33. Таблица 33. Затраты на производство единицы продукции по корпорации
Средние затраты на единицу продукции корпорации составляют 12 руб. Риск превышения затрат на единицу продукции составляет 1,632 руб. – величину среднего квадратического отклонения. Общие производственные затраты в месяц составляют в среднем: 12 * 6000 = 72 000 руб. Свойство 1. Уменьшение или увеличение всех значений признака на одинаковую величину не меняет величины дисперсии, среднего квадратического отклонения и размаха вариации. Проверим, как повлияет на величину показателей вариации снижение затрат на единицу продукции на 2 руб. в результате оптимизации производственных процессов при неизменном объеме производства (табл. 34). Таблица 34. Затраты на производство единицы продукции по корпорации
Как мы видим, при снижении затрат на производство единицы продукции на 2 руб. риск превышения затрат на единицу продукции остался неизменным – 1,63 руб., также как и величины дисперсии, и размаха вариации. Но это не означает, что корпорации не нужно оптимизировать производство: за счет снижения затрат на единицу общие производственные затраты корпорации составили: 10 * 6000 = 60 000 руб., что на 12 тыс. руб. (или на 16,6 %) меньше, чем было до оптимизации – 72 000 руб. Свойство 2. Увеличение всех значений признака в k раз (k – любое число) увеличивает дисперсию в k2 раз, среднее квадратическое отклонение и размах – в k раз. (Если k<0, то коэффициент берется по модулю). Коэффициент вариации при этом не меняется. Предположим условную ситуацию, что все затраты на единицу продукции в результате двойного удорожания цен на сырье выросли в два раза. Как это (при неизменном объеме производства) отразится на риске увеличения затрат на единицу продукции по сравнению с исходным уровнем (по данным табл. 32)? Проверим расчеты (табл. 35). Таблица 35. Затраты на производство единицы продукции по корпорации
Как мы видим, при увеличении затрат на производство единицы продукции в 2 раза размах вариации вырос в 2 раза. Риск превышения затрат на единицу продукции составляет 3,266 руб., т.е. также в два раза больше, чем первоначальный 1,632 руб. (3,266 : 1,632 = 2). Соответственно, для получения оценки риска от увеличения затрат на единицу продукции в два раза достаточно исходное среднее квадратическое отклонение 1,632 умножить на 2. Размер дисперсии составил 10,6667. Это в 4 раза больше, т.е. в 22 раз, чем исходное значение (10,6667 : 2,6667 = 3,9999 ≈ 4 (из-за округлений)). Коэффициент вариации остался неизменным – 13,6 %, как и до двукратного увеличения затрат на единицу произведенной продукции. Свойство 3.Дисперсия отклонений значений признака от произвольного числа А (Xi– А)2 увеличивает дисперсию отклонений от средней Для иллюстрации свойства предположим, что руководство корпорации решило оценить уровень риска при условии, что средние затраты на единицу продукции в корпорации остались бы на уровне прошлого года – 15 руб. Проверим действие свойства, рассчитав отклонения затрат на единицу продукции от 15 (табл. 36). Таблица 36. Затраты на производство единицы продукции по корпорации
где Свойство подтверждено: 11,6667 - 2,6667 = 9 = (12 - 15)2 = (-3)2 Вопросы для самопроверки: 1. Что такое изменчивость, или вариация данных? 2. Какой показатель и почему используют для оценки изменчивости? 3. Что характеризует среднее квадратическое отклонение? В каких единицах оно измеряется? 4. В каких случаях для расчета показателей вариации используются взвешенные формулы? 5. Для чего применяется коэффициент вариации? В каких единицах он измеряется? 6. Как изменится дисперсия, если все значения признака увеличить на 100? 7. Как отразится на величине коэффициента вариации сокращение каждого значения признака в 4 раза? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006. 5. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания: Задание 1. По данным о ценах на финансовый актив нескольких компаний-конкурентов определите, является ли предлагаемая вашей компанией цена 24 тыс. руб. конкурентоспособной относительно цен конкурентов. Является ли отличие цены вашей компании от цен конкурентов типичным? Следует ли вашей компании каким-либо образом изменить установленную цену, если компания придерживается стратегии ценовой консолидации с конкурентами? Каким будет среднеквадратическое отклонение цены актива по всем конкурентам, если все компании решат увеличить первоначальную цену актива на 20 %?
Задание 2. Оцените однородность распределения строительных фирм по объему инвестиций по следующим данным:
Задание 3. Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя величина – 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
