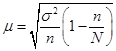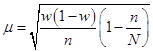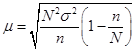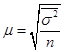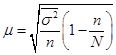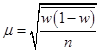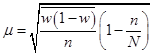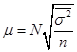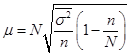цйу. Документ Microsoft Word (2). Программа дисциплины Статистика
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
|
Тема 7. Выборочный метод наблюдения в статистических исследованиях Цель изучениятемы состоитв формировании системы знаний и компетенций о видах выборочного наблюдения, применяемого в статистических исследованиях, его преимуществах, основных показателях и способах их расчета. В результате успешного освоения темы Вы: Узнаете: · какие виды выборочного наблюдения существуют и для чего они применяются; · основные задачи выборочного наблюдения и преимущества его применения; · какими показателями характеризуются результаты выборочного наблюдения; · что такое средняя и предельная ошибка выборки и каковы особенности их расчета для выборок различных видов. Приобретете компетенции: · владение методами количественного анализа и моделирования, теоретического и экспериментального исследования; · понимание роли и значения информации в развитии современного общества и экономических знаний; · владение основными методами, способами и средствами получения, хранения, переработки информации; · способность анализировать финансовую отчетность и принимать обоснованные решения; · умение применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели; · умение определять вид выборки и рассчитывать ее необходимый объем; · способность распространять результаты выборочного наблюдения на генеральную совокупность и формулировать выводы по полученным результатам. В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях: · выборочное наблюдение; · генеральная и выборочная совокупность; · повторный и бесповторный отбор; · собственно случайная выборка, таблица случайных чисел; · механическая (систематическая) выборка; · стратифицированная случайная выборка; · средняя ошибка выборки; · предельная ошибка выборки. Вопросы темы: 1. Теоретические основы выборочного наблюдения. 2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность. 3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли. 4. Определение объема выборочной совокупности. Теоретический материал по теме Вопрос 1. Теоретические основы выборочного наблюдения. Выборочным наблюдением называется такое несплошное обследование, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность. Полученные статистические характеристики сопровождаются указанием на точность оценивания, которая зависит от репрезентативности (представительности) выбранной совокупности, т.е. от того, насколько качественно она отражает закономерность генеральной совокупности. Генеральной совокупностью (основой выборки) называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Количество единиц генеральной совокупности обозначается через N. Выборочная совокупность – это небольшой набор объектов, извлеченных из генеральной совокупности по определенным правилам. Количество единиц выборочной совокупности обозначается через n. Доля выборочных единиц в объеме генеральной совокупности, выраженная в процентах, называется долей отбора (процентом выборки) и определяется следующим образом: Например, при объеме генеральной совокупности в 2 000 единиц и выборочной в 500 единиц, говорят о 25-процентной выборке. Единицами отбора называют элементы отбора при формировании выборочной совокупности. Единицей наблюдения выступает объект, признаки которого подлежат регистрации. Единица наблюдения может не совпадать с единицей отбора. Если исследуется количественный признак, то непосредственной задачей выборочного наблюдения выступает оценка среднего и суммарного значений. Генеральное среднее значение определяется по данным генеральной совокупности и обозначается через . Формула для его расчета имеет вид: 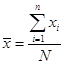 (49) (49)Выборочное среднее ( ) является оценкой генерального среднего и определяется по формуле: 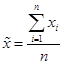 (50) (50)Генеральная дисперсия единиц количественного признака определяется по формуле: 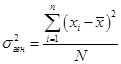 (51) (51)Так как генеральная дисперсия по большей части в ходе исследования остается неизвестной, то условно ее принимают равной дисперсии, рассчитываемой по выборочным данным: 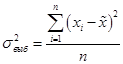 (52) (52)При малочисленных выборках (менее 30 объектов) в формулу необходимо внести поправку – уменьшить знаменатель на единицу: Помимо определения характеристик количественных признаков можно произвести оценку характеристик альтернативных показателей. Численность единиц, обладающих изучаемыми признаками в генеральной совокупности, обозначается через M, а в выборочной – через m. Тогда доля единиц, обладающих исследуемыми признаками в генеральной совокупности, определяется как: где М – численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака. В выборочной совокупности: где m – численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака. Генеральная дисперсия доли альтернативного признака рассчитывается по формуле: где p – генеральная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака во всей генеральной совокупности; q – доля единиц, не обладающих исследуемым признаком (q = 1– p). Выборочная дисперсия доли: где w – выборочная доля, то есть доля единиц, обладающих определенным вариантом или вариантами изучаемого признака в выборочной совокупности. Основные преимущества выборочного метода по сравнению со сплошным заключаются в следующем: 1. Быстрота получения результатов обследования за счет снижения объема наблюдаемой совокупности из-за отбора и обработки данных только по определенной части ее единиц. 2. Значительное снижение стоимости наблюдения. 3. Возможность лучшей организации проведения обследования за счет минимизации влияния ошибокрегистрации в силу меньшего количества обследуемых единиц генеральной совокупности. 4. Возможность расширения программы наблюдения в силу снижения численности наблюдаемых единиц и возможности включения в программу исследования более широкого круга регистрируемых признаков. 5. Возможность использования в случаях, когда проведение сплошного наблюдения методологически невозможно. Например, при статистическом исследовании качества продукции выборочное наблюдение становится единственно возможным, так как данные виды исследования связаны с порчей или уничтожением продукции. Если генеральная совокупность объектов изучения бесконечно велика и нет возможности обследовать каждую единицу, также используется выборочный метод наблюдения (например, маркетинговые обследования покупателей, изучение пассажиропотоков и т.п.). Наиболее существенным недостатком выборочного наблюдения является наличие ошибок репрезентативности – ситуаций, при которых выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Это может быть вызвано наличием как случайных, так и систематических ошибок репрезентативности,связанныхс нарушением принципов формирования выборочной совокупности. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Вопрос 2. Виды выборочного наблюдения. Способы и методы отбора единиц в выборочную совокупность. В зависимости от состава и структуры генеральной совокупности различают виды выборок и способы отбора единиц. Способ отбора единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. Число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется. На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности неизвестен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков. Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Так, например, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию. При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке. Различают следующие методы отбора единиц из генеральной совокупности: · метод индивидуального отбора, при котором в выборочную совокупность извлекаются отдельные единицы генеральной совокупности, например: при обследовании коммерческих банков – банки, при обследовании населения – конкретные люди и т.д. Применяется при организации собственно случайной, механической и типической выборок; · метод группового отбора предполагает извлечение единиц из генеральной совокупности группами, например, бригадами, микрорайонами и т.д. Такой отбор применяется при серийной выборке; · метод комбинированного отбора, при котором вначале отбираются группы единиц, а затем из них случайным образом извлекаются конкретные единицы совокупности. Каждый метод отбора может быть реализован как повторным, так и бесповторным способами. Выбор вида выборок определяется задачами исследования и, прежде всего, полнотой и особенностями информации, которой располагает исследователь об объекте наблюдения. Наиболее распространенными видами выборок, применяемыми на практике, являются: · собственно случайная выборка; · механическая (систематическая) выборка; · типическая (стратифицированная, расслоенная) выборка. Собственно случайная выборка заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков. Простая случайная выборка строится исходя из следующих правил: 1) каждый объект генеральной совокупности имеет одинаковую вероятность быть отобранным; 2) объекты отбираются независимо друг от друга. Одним из способов извлечения случайной выборки является применение таблицы случайных чисел для получения номера каждого отобранного объекта генеральной совокупности. Сам объект затем находят в основе выборки. Таблица случайных чисел представляет собой организованную в виде таблицы последовательность чисел, в которой каждая из цифр от 0 до 9 встречается независимо друг от друга с вероятностью 1/10. Составить таблицы случайных чисел можно, например, с помощью датчика случайных чисел. Его содержат все современные статистические пакеты, а также MS Excel («Вставка функций» – «Математические» – «Случайное число»). Для проведения отбора могут быть использованы цифры любого столбца данной таблицы, при этом необходимо учитывать объем генеральной совокупности. Для получения механической (систематической) выборки необходимо выбрать в основе выборки одну случайную начальную точку (за счет этого вносится в выборку элемент случайности) и затем производить отбор элементов в основе выборки с некоторым постоянным шагом. При таком способе отбора генеральная совокупность делится на столько групп, сколько единиц наблюдения должно войти в выборку, и из каждой группы отбирается одна единица. Единицы генеральной совокупности нумеруются числами от 1 до N, после чего отбираются каждые N/n-е объекты для выборки, находящиеся на равном расстоянии друг от друга (n – объем выборки, N – объем генеральной совокупности). Величина N/n называется шагом, или интервалом отбора между выбираемыми элементами. Например, если для 1000 единиц требуется создать 5-процентную выборочную совокупность, то объем выборки будет 50 единиц, интервал отбора составит 1000 / 50 = 20. Это значит, что в выборку попадет каждый 20-й элемент генеральной совокупности. Существуют два способа формирования основы механической выборки: по неранжированным (по отношению к изучаемым признакам) данным и по ранжированной генеральной совокупности. В первом случае результаты механического отбора будут являться реализацией случайного бесповторного отбора, так как единицы наблюдения располагаются в случайном порядке. Усилить данную случайность возможно выбором начальной точки отсчета случайным образом из интервала, соответствующего первому шагу отбора. Во втором случае единицы наблюдения определенным образом упорядочиваются по величине изучаемого признака и отбор осуществляется в соответствии с его шагом N/n, начиная с единицы, являющейся серединой первого интервала. Однако метод систематического отбора имеет серьезные недостатки из-за невозможности оценить точность получаемой выборки. Недопустимо использование систематической выборки в случае повторяемости некоторого ее фрагмента, который по размеру соответствует и интервалу отбора. Например, если во время упаковки на конвейере каждому 20-му изделию уделяют особое внимание и по воле случая при шаге выборки № 20 вы отберете в свою систематическую выборку именно эти изделия, то результаты систематической выборки будут полностью бесполезны в отношении репрезентативности качества других обычных изделий. Стратифицированную случайную выборку применяют, когда генеральная совокупность содержит ясные, известные, легко идентифицированные группы. Такие группы также называются слоями (стратами), в связи с чем типический отбор называют также стратифицированным, или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п. Стратифицированную выборку получают путем осуществления случайной выборки отдельно в каждой страте генеральной совокупности. Существуют следующие два вида организации отбора внутри типической группы: · пропорционально объему типических групп; · пропорционально степени колеблемости значений признака у единиц наблюдения в группах. При проведении отбора пропорционально объему типических групп число единиц, подлежащих отбору из каждой группы, определяется следующим образом: 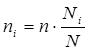 , (58) , (58)где ni – количество извлекаемых единиц для выборки из i-й типической группы; n – общий объем выборки; Ni – количество единиц генеральной совокупности, составивших i-ю типическую группу; N – общее количество единиц генеральной совокупности. Размеры выборки для каждой из страт могут быть разными. Для одних страт процесс отбора может быть сложнее и дороже, чем для других, и для этих страт используются меньшие по размеру выборки. Другие страты могут иметь большую изменчивость, и поэтому для них требуется использовать большие по размеру выборки. Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым. Вопрос 3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли. Из одной и той же генеральной совокупности объемом N единиц можно извлечь множество различных выборок заданного объема n. Тогда в каждом случае рассчитанные отклонения выборочных характеристик от генеральных будут различны. Если определить среднюю из ошибок всех возможных выборок заданного объема, то получим их обобщающую характеристику – среднюю ошибку выборки (μ), которая показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Ошибка выборки, или отклонение выборочной средней от средней генеральной, находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности и в обратной зависимости – от объема выборки. Таким образом, среднюю ошибку выборки можно представить как При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующая зависимость: В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки. При достаточно большом объеме выборки отношение близко к 1. При бесповторном отборе необходимо учитывать поправку на конечность совокупности При стратифицированной выборке в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, поэтому при типизации генеральной совокупности исключается влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий. Формулы для определения средней ошибки выборки индивидуальны для различных способов отбора (повторного и бесповторного), видов используемых выборок и оцениваемых статистических показателей (таблица 37). Таблица 37. Формулы для расчета средней ошибки выборки (μ)
Для определения возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки (Δ), которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы: (61) Уровень предельной ошибки выборки зависит от следующих факторов: · от степени вариации единиц генеральной совокупности; · от объема выборки; · от выбранных схем отбора – повторного и бесповторного; · от уровня доверительной вероятности. Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки при достаточно большом объеме выборочной совокупности подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа. Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках. Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента. При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Например, если при расчете предельной ошибки выборки мы используем значение t = 2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки. Построение доверительных интервалов для генеральной средней и доли осуществляется следующим образом: Определение границ генеральной средней и доли состоит из следующих этапов: · нахождение выборочного значения средней (или доли); · определение средней ошибки выборки в соответствии с выбранной схемой отбора и видом выборки; · задание доверительной вероятности Р и определение коэффициента доверия t; · вычисление предельной ошибки выборки ; · построение доверительного интервала для среднего (доли). Пример 1. Для изучения среднего размера расходов на стоматологическую страховку, которую готовы заплатить служащие банка в год, из 1350 банковских работников было обследовано 810 человек методом случайного повторного отбора. В результате были получены следующие данные (таблица 38). Таблица 38. Результаты выборочного обследования банковских служащих на предмет размера расходов на стоматологическую страховку
Определите с вероятностью 0,954: а) предельную ошибку выборки и границы для генеральной средней; б) в каких границах находится генеральная доля банковских служащих, готовых израсходовать на страховку не более 1000 долл. Решение: 1. По результатам выборочного обследования рассчитаем среднее значение и дисперсию выборочной совокупности, для чего необходимо рассчитать середины интервалов группировочного признака «размер расходов» (табл. 38). Для удобства расчетов построим вспомогательную таблицу 39. Таблица 39. Вспомогательная таблица для расчета среднего размера страховки и дисперсии
Выборочная средняя составит: Выборочная дисперсия изучаемого признака: 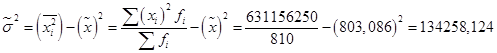 Выборочное среднеквадратическое отклонение составит: 2. Определим среднюю ошибку повторной случайной выборки: 3. Определим предельную ошибку выборки с заданной вероятностью. Для этого по таблице значений вероятности функции нормального распределения находим величину коэффициента доверия t, соответствующего вероятности 0,954. При F(t) = 0,954, t = 2. Предельная ошибка выборки с вероятностью 0,954 равна: Найдем доверительные границы для среднего значения размера страховки: 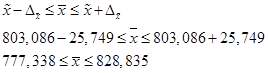 Таким образом, в 954 случаях из 1000 средний объем денежных средств, которые служащие готовы потратить на стоматологическую страховку в год, не будет превышать 828,8 долл. и не будет меньшим, чем 777,3 долл. Теперь определим, в каких границах в генеральной совокупности находится доля банковских служащих, готовых израсходовать на страховку не более 1000 долл. 4. Рассчитаем выборочную долю. Количество банковских работников, готовых потратить на страховку не более 1000 долл., в выборочной совокупности составляет 550 ед., следовательно: m = 550, n = 810, w = m / n= 550 / 810 = 0,679. 5. Рассчитаем выборочную дисперсию доли: 6. Средняя ошибка выборки при использовании повторной схемы отбора составит: Предположим, что была использована бесповторная схема отбора. Тогда средняя ошибка выборки с учетом поправки на конечность совокупности составит: 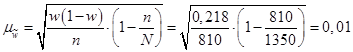 7. Определим предельную ошибку выборки. При значении вероятности р = 0,954 по таблице нормального распределения получаем значение коэффициента доверия t = 2. 8. Определим границы для генеральной доли с вероятностью 95,4 % для бесповторного отбора: 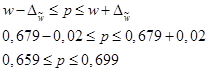 Следовательно, с вероятностью 0,954 можно утверждать, что в генеральной совокупности доля сотрудников, готовых израсходовать на стоматологическую страховку не более 1 000 долл. в год, не меньше 65,9 % и не больше 69,9 %. Пример 2. Руководстворегионально-распределенной корпорации дало поручение провести исследование частоты обращения сотрудников к недавно введенной в эксплуатацию корпоративной базе знаний, содержащей сведения об истории реализации корпорацией проектов, инструкции по действию и ответы на вопросы о действиях сотрудника в сложных производственных ситуациях, экспресс-курсы повышения квалификации и другую справочную информацию. Для этих целей была использована 15 % бесповторная типическая выборка, типические группы которой соответствуют региональному отделению. При отборе, пропорциональному объему типических групп, получены данные (таблица 40). Таблица 40. Результаты обследования сотрудников корпорации
Общий объем выборочной совокупности составит: Количество сотрудников, которое необходимо обследовать в каждом региональном отделении, определим согласно формуле: 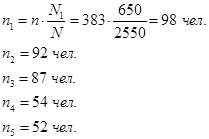 1. Выборочная средняя, основываясь на значениях средних типических групп, составит: 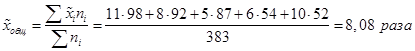 2. Средняя из внутригрупповых дисперсий равна: 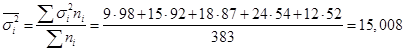 3. Средняя ошибка выборки: 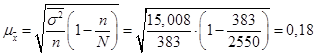 С вероятностью 0,954 находим предельную ошибку выборки: 4. Доверительные границы для среднего находятся в пределах: Вопрос 4. Определение объема выборочной совокупности. Важным вопросом, особенно на этапе проектирования выборочного наблюдения, является определение объема выборочной совокупности. Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Затраты всех ресурсов на 20–30 %-ное выборочное наблюдение уже сопоставимы с расходами на сплошное обследование. При этом не следует забывать, что статистические характеристики, полученные по выборочной совокупности, всегда имеют вероятностную основу и всегда будут уступать результатам сплошного наблюдения по точности и надежности. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности. Предельную ошибку повторной собственно случайной выборки можно записать через среднюю ошибку: Отсюда можно вывести формулу для определения необходимого объема собственно случайной повторной выборки: 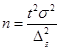 (64) (64)Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 598,1 единицы, то для достижения желаемого результата обследованием должны быть охвачены 599 единиц. Пример 3. Вам необходимо провести исследование с вероятностью 95,4 %, посвященное оценке удовлетворенности качеством работы менеджеров, отвечающих за поддержку клиентов по телефону. Качество обслуживания оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 5 %. Какое минимальное количество респондентов вам необходимо опросить в порядке собственно случайной повторной выборки для решения данной проблемы? Решение: Поскольку при вероятности 0,954 значение t = 2, находим необходимый объем выборки: Следовательно, обследованию необходимо подвергнуть не менее 400 респондентов на предмет оценки удовлетворенности качеством работы менеджеров из службы поддержки. В соответствии с формулой 16 необходимый объем выборки будет тем больше, чем выше заданный уровень вероятности и чем сильнее варьирует наблюдаемый признак. В то же время повышение допустимой предельной ошибки выборки приводит к снижению необходимого ее объема. При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение: Это значение подставляется в формулу 64 в качестве значения дисперсии. Необходимый объем собственно случайной бесповторной выборки определяется по следующей формуле: При этом важно помнить, что в процессе проведения вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц. Например, подставив в данную формулу общее количество заказов, выраженное в тысячах единиц, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах единиц, как это иногда бывает в других расчетах. Результат вычислений будет неверен. Пример 4. Требуется определить объем выборки для исследования удовлетворенности постоянных клиентов качеством работы персональных менеджеров с вероятностью 95,4 %. Качество работы оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 0,05. Какое минимальное количество постоянных клиентов вам необходимо опросить в порядке собственно случайной бесповторной выборки, если общий список постоянных клиентов компании составляет 1000 человек? Решение: Следовательно, для обеспечения репрезентативности данных исследования выборочному обследованию методом бесповторного отбора необходимо подвергнуть не менее 286 постоянных клиентов компании. Для определения численности механической выборки используют формулы, применяемые при собственно случайном бесповторном отборе. При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление в меньшую сторону для получения целочисленного интервала отбора. Пример 5. Вы контролируете работу 284 супермаркетов вашего района. Определим, сколько из них необходимо отобрать в порядке механического отбора для выявления нарушений политики вашей компании с ошибкой +/-2 нарушения и с вероятностью 0,95. По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение численности нарушений составляет 3 единицы. Решение: Расчет проведем, используя формулу 66: С учетом полученного необходимого объема выборки (9 супермаркетов) определим интервал отбора: 284 / 9 = 31,56. Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема. Следовательно, в нашем примере, из общего списка супермаркетов необходимо отобрать для обследования каждый 31-й магазин. При этом процент отбора составит 3,2 % (100 % / 31, или 9 / 284). Вопросы для самопроверки: 1. Какие преимущества и недостатки по сравнению со сплошным наблюдением имеет выборочное наблюдение? 2. В чем отличие бесповторного от повторного отбора? 3. Что показывает предельная ошибка выборки? От каких основных факторов зависит ее уровень? 4. Что показывает средняя ошибка выборки? 5. Что понимается под доверительной вероятностью и коэффициентом доверия? Какая существует между ними зависимость? 6. В чем отличие механического отбора от случайного? 7. Какие проблемы возникают при использовании систематической выборки? 8. Что представляет собой стратифицированная выборка? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006. 3. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 5. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания: Задание 1. Определите вид выборки – собственно случайная, механическая, стратифицированная – использованный при проведении исследования, указанного в таблице.
Задание 2. Определите необходимый объем выборки для обследования среднедушевых денежных доходов населения области методом собственно случайного повторного отбора, чтобы с вероятностью 0,997 предельная ошибка выборки не превышала 300 руб, если известно, что среднее квадратическое отклонение величины среднедушевого денежного дохода составляет 2783 руб. Задание 3. Количество корпоративных клиентов-юридических лиц банка составляет 750. Планируется проведение механического выборочного обследования с целью определения уровня удовлетворенности работой новой системы интернет-банкинга (в баллах по пятибалльной системе). Определите сколько и каких клиентов из общего списка необходимо опросить, чтобы с вероятностью 0,9545 предельная ошибка не превысила 0,3 балла, если известно, что дисперсия оценок системы интернет-банкинга клиентами составляет 3,85. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||