цйу. Документ Microsoft Word (2). Программа дисциплины Статистика
 Скачать 1.87 Mb.
|
|
=PEARSON(массив 1; массив 2) (75) Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение: Массив 1 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения факторного показателя x; Массив 2 – диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y. Вводить команду PEARSON можно в командной строке редактора или непосредственно в ячейке, в которой мы хотим получить значение коэффициента взаимосвязи. Проиллюстрируем использование MS Excel для расчета взаимосвязи показателей примера 1 (таблица 49). Исходные данные о товарообороте и количестве клиентов крупнейших туристических компаний РФ в 2011 г. оформлены в MS Excel в виде таблицы, представленной на рис. 29. 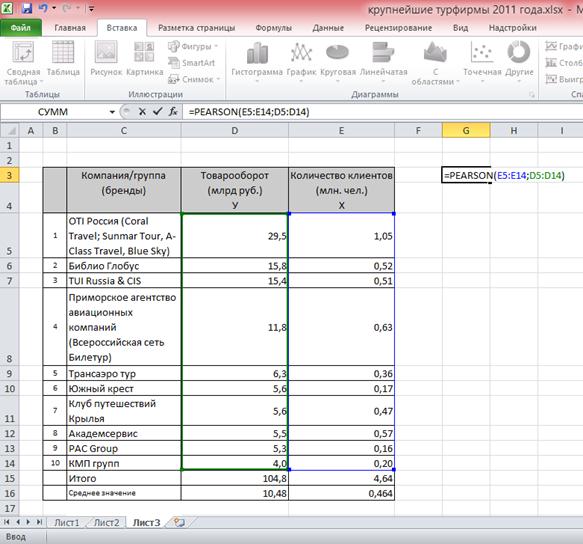 Рис. 29. Иллюстрация применения команды PEARSON в MS Excel В этой таблице в столбце Е, а именно в ячейках с Е5 по Е14, указаны данные о количестве клиентов компаний – показатель x, а в столбце D ячейки D5:D14 содержат данные о товарообороте туркомпаний – показатель y. Очень важно проверить, чтобы формат ячеек, содержащих данные, был именно числовым, а не текстовым, поскольку текстовые и пустые ячейки при расчете коэффициента корреляции Пирсона в MS Excel не учитываются, что искажает результат вычислений и не позволяет правильно оценить взаимосвязь между показателями! Установим курсор в ячейку G3 и воспользуемся командой PEARSON. Для этого в ячейку мы введем следующие символы: «=PEARSON(» (кавычки не вводятся!) (рис. 29). После ввода начальных символов команды MS Excel выведет на экран для подсказки внизу ячейки синтаксис формулы и будет ждать действий пользователя по заданию ее параметров. Далее произведем следующие действия: · для задания параметра «массив1» выделим курсором область ячеек от E5 до E14, которая содержит значения количества клиентов – факторного показателя x; · после этого наберем в нашей ячейке G3 или в командной строке MS Excel символ «;» (точка с запятой); · для задания параметра «массив2» выделим курсором область ячеек от D5 до D14, где указаны значения товарооборота туркомпаний – результативного показателя y. Если все действия были совершены верно, то подстрочная подсказка исчезнет, а в ячейке и в командной строке MS Excel отобразится функция PEARSON с введенными пользователем параметрами (рис. 29). Убедившись, что параметры команды заданы верно, нажмем на клавишу Enter и увидим (рис. 30), что в выбранной нами ячейке G3 указано значение 0,855074. 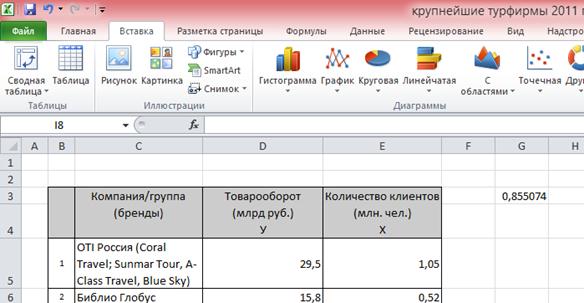 Рис. 30. Иллюстрация результата применения команды PEARSON в MS Excel Важный момент: если нажать клавишу Enter до момента ввода параметра «массив2» или допустить ошибку при указании диапазонов данных, так что массивы получатся не равными по количеству объектов (например, в параметре «массив1» указать (E5:E14), а в «массив2» – (D6:D13)), то MS Excel вместо результата выведет в выбранной вами ячейке значение «#Н/Д». Вопрос 2. Регрессионный анализ. Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (результативного признака) обусловлено влиянием одной или нескольких независимых величин (факторных признаков), и в выборе математической модели функции, при помощи которой эту взаимосвязь можно описать. Цель моделирования – получить аналитическое выражение взаимосвязи в виде математической функции, которая позволяет предсказывать значение одной переменной (признака) на основании другой. Математическую функцию, описывающую зависимость у от х, называют уравнением регрессии, а параметры этой модели – параметрами, или коэффициентами регрессии. Уравнение регрессии описывает теоретическую линию, вокруг которой концентрируются точки на диаграмме рассеяния и которая определяет основное направление взаимосвязи между признаками x и у. (рис. 31).  Рис. 31. Диаграмма рассеяния (поле корреляции) Для построения уравнения регрессии необходимо выполнение следующих требований: · факторный и результативный признаки должны иметь количественное выражение; · совокупность исходных данных должна быть однородной, значительной по объему и математически описываться непрерывной функцией; · взаимосвязи между явлениями должны описываться линейной или приводимой к линейной форме зависимостью. Соблюдение данных требований позволяет построить статистическую модель, наилучшим образом описывающую взаимосвязь между признаками. Парная линейная регрессия позволяет получить аналитическое выражение связи между двумя признаками – результативным и факторным, описываемое уравнением прямой линии. Уравнение парной линейной регрессии имеет вид:  , (76)где – расчетное значение результативного признака y при определенном значении факторного признака x; а0 показывает усредненное влияние на результативный признак не учтенных в уравнении факторных признаков; а1 – коэффициент регрессии, показывающий, насколько в среднем изменится значение результативного признака при изменении факторного на единицу собственного измерения. Определить тип уравнения можно, исследуя зависимость графически. Существуют другие способы, позволяющие определить вид уравнения связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, между ними существует линейная связь, а при обратной зависимости – гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая, или степенная регрессия. Оценка параметров уравнения регрессии a0 и a1 осуществляется методом наименьших квадратов. Этот метод позволяет найти такие параметры модели, при которых расчетные значения были бы максимально близки к исходным значениям у. Поскольку в статистке за меру отличия чаще всего принимается отклонение, то методом наименьших квадратов находятся параметры модели, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по линейному уравнению регрессии. Для нахождения параметров линейной парной регрессии методом наименьших квадратов необходимо решить систему нормальных уравнений, которая имеет следующий вид: 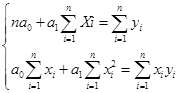 (78)где n – объем исследуемой совокупности (число единиц наблюдения); xi, уi – значения факторного и результативного признаков у i-й единицы. Рассчитать параметры линейного уравнения регрессии можно при помощи стандартного табличного редактора MS Excel. Для начала напомним, что с точки зрения математики линейная функция – это прямая линия, которая проходит в двумерной системе координат. Параметр a0 – это точка, в которой прямая линия пересекает ось y, т.е. в этой точке значение х = 0. За расположение прямой в системе координат отвечает угол наклона прямой линии (отношение величины подъема линии к ее длине), а именно – параметр a1: если наклон имеет знак «+», то линия поднимается слева на право, если наклон равен «0» – линия идет горизонтально оси х, а если знак «-», то линия опускается слева на право. В MS Excel существует встроенная функция «НАКЛОН», которая позволяет легко получить значение коэффициента a1 по исходным данным y и х методом наименьших квадратов. Синтаксис этой команды имеет следующий вид: =НАКЛОН(известные значения_y; известные значения_х) (79) Параметры команды, указанные в скобочках, задаются пользователем и имеют следующее значение: Известные значения_y– диапазон данных в исходной таблице, как правило, в столбце, в котором указаны значения результативного показателя y; Известные значения_х – диапазон данных в исходной таблице, как правило в столбце, в котором указаны значения факторного показателя x. Диапазоны данных задаются пользователем и очень важно сделать это правильно, поскольку, например, перепутав местами диапазоны х и y, Вы дадите программе команду вычислять коэффициент регрессии уже для другого случая взаимосвязи – исследования влияния значений y на значения х, что не входит в наши планы и неверно, поскольку y будет рассматриваться программой как факторный признак, а не как признак-результат. Расчет параметра a0 в среде MS Excel также упрощается. Для начала необходимо рассчитать средние значения показателей y и х, вычислить параметр a1, а затем произвести расчет параметра a0 по следующей формуле:  (80)Таким образом, расчет параметров уравнения регрессии при помощи MS Excel зависит от точности действий пользователя при вводе исходных данных и задании параметров специальной встроенной для этого команды-функции. Пример 2. Быстродействие компьютеров, объединенных в сеть, при возникновении перегрузок, как правило, снижается. Естественно, чем больше загрузка компьютера x, тем большим должно быть время реакции y. Под временем реакции понимается интервал с момента нажатия клавиши Enter до момента выдачи компьютером ответа на введенный вами запрос. Таблица 50. Показатели быстродействия компьютера
Предположим наличие линейной зависимости между рассматриваемыми показателями. Построим расчетную таблицу для определения параметров линейного уравнения регрессии времени реакции компьютера (табл. 51). Таблица 51. Расчетная таблица для определения параметров уравнения регрессии между временем реакции и процентом загрузки компьютера от полной мощности
Система нормальных уравнений для данного примера имеет вид: 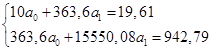 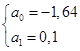 Следовательно,  .Значения в таблице 51 получены путем подстановки значений факторного признака хi(загрузка компьютера) в уравнение регрессии 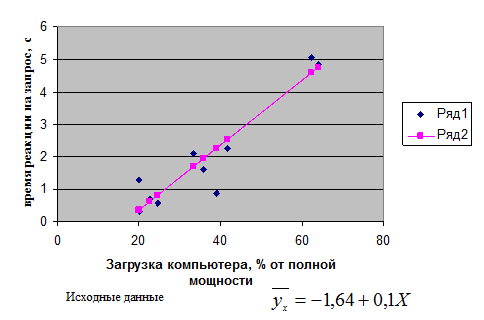. На рисунке 32 полученные нами расчетные значения нанесены на диаграмму рассеяния, соединены между собой и образуют прямую линию, обозначающую область концентрации облака точек, построенных по исходным значениям х и у. Рис. 32. Зависимость скорости реакции компьютера от состояния его загрузки Проиллюстрируем расчет параметров линейного уравнения регрессии при помощи МS Excel. 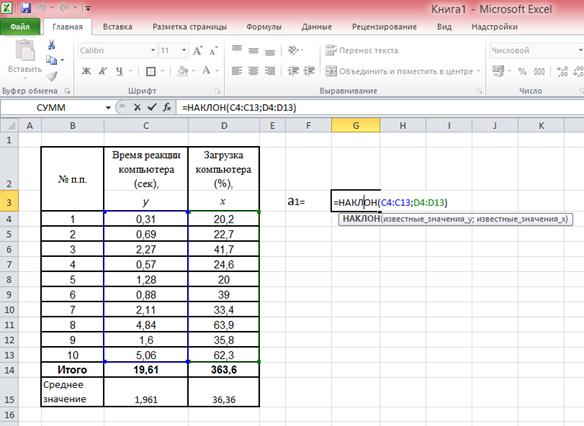 Рис. 33. Иллюстрация применения команды-функции «НАКЛОН» в MS Excel для расчета коэффициента регрессии а1 На рисунке 33 показано, что пользователь рассчитывает значение коэффициента регрессии а1 в ячейке G3. Для этого он предварительно ввел исходные данные в таблицу (столбцы С и D), затем кликнул на ячейку G3, ввел с клавиатуры «=НАКЛОН(», далее, следуя подсказкам Excel, указал известные значения y – это диапазон (С4:С13), затем указал известные значения x – диапазон (D4:D13), после этого ввел с клавиатуры символ «)» (чтобы соблюсти синтаксис команды). Ему остается только нажать клавишу Enter, чтобы увидеть на экране искомое значение коэффициента. На рис. 34, иллюстрирующем пример расчета коэффициента а0 в MS Excel, видно, что значение коэффициента регрессии а1 – содержимое ячейки G3 – составляет 0,10. 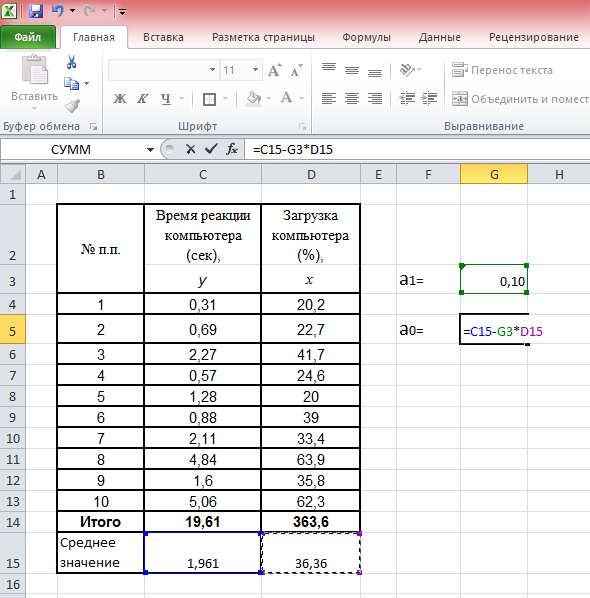 Рис. 34. Иллюстрация расчета параметра а0 в MS Excel после применения команды-функции «НАКЛОН» для расчета коэффициента регрессии а1 Величина а1 необходима для расчета параметра а0 по формуле . Из рисунка 34. видно, что пользователь предварительно рассчитал средние значения показателей y и х и перешел к расчету коэффициента а0 в ячейке G5. Он ввел в эту ячейку символ «=» и согласно формуле задал Excel последовательность действий: «возьми содержимое ячейки C15 (среднее значение y), вычти из него произведение ячейки G3 (коэффициент a1) на ячейку D15 (среднее значение х)». Значение коэффициента а0 составляет -1,64, следовательно:  Коэффициент регрессии a1 = 0,1 означает, что при увеличении загрузки компьютерных мощностей на 1 % время реакции компьютера повышается в среднем на 0,1 сек. Данную оценку связи можно использовать для прогнозирования времени реакции компьютерапри соответствующем проценте загрузке. Например, при загрузке компьютера на 50 % время его реакции составит  сек.Линейные модели являются основными при определении аналитического выражения связи. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т.д. Если связь между факторным и результативным признаками описывается уравнением параболы второго порядка вида:  , (81)то система нормальных уравнений имеет вид: 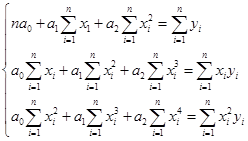 (82)Оценка обратной связи осуществляется на основании гиперболы вида:  (83)Система нормальных уравнений для нахождения параметров гиперболы: 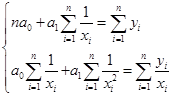 (84)При нелинейной зависимости между признаками для измерения тесноты связи между ними вычисляют теоретическое корреляционное отношение: 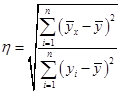 (85)Корреляционное отношение изменяется в пределах от 0 до 1  . Его величина интерпретируется по стандартным критериям оценки коэффициента корреляции.Пример 3. Рассмотрим данные об объеме производства вишни в фермерских хозяйствах и цене вишни. Таблица 52. Объем производства и фермерская цена вишни хозяйств области
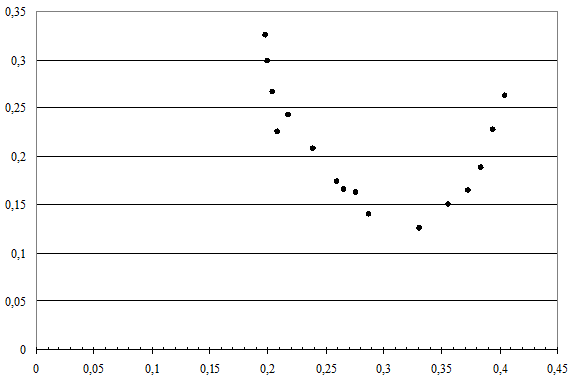 Рис. 35. Диаграмма рассеяния, характеризующая взаимосвязь между объемом производства вишни и фермерской ценой на нее Как правило, зависимость между производством и ценой товара нелинейная. Диаграмма рассеяния, представленная на рис. 35, иллюстрирует пример нелинейной взаимосвязи, выраженной уравнением параболы второго порядка. Построим расчетную таблицу для определения параметров нелинейного уравнения регрессии, выраженного параболической функцией (табл. 53). Таблица 53. Расчетная таблица для нахождения параметров уравнения регрессии
Система нормальных уравнений для данного примера имеет вид (согласно формуле 82): 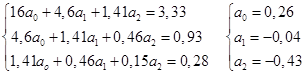 Следовательно,  .Значения в таблице 53 получены путем пошаговой подстановки значений факторного признака хi(объем производства вишни) в уравнение регрессии. Коэффициент регрессии a1 = -0,04 означает, что при увеличении объема производства вишни на 1 тыс. т фермерская цена будет в среднем снижаться на 0,04 тыс. долл. Определим тесноту связи между объемом производства и фермерской ценой вишни. Все расчеты представим во вспомогательной табл. 54. Таблица 54. Расчетная таблица для определения теоретического корреляционного отношения
Теоретическое корреляционное отношение согласно формуле 85 составит:  Таким образом, связь между объемом производства вишни и фермерской ценой можно признать умеренной. Невысокое значение теоретического корреляционного отношения в данном случае оправдано, поскольку кроме объема производства на устанавливаемую фермерами цену оказывают сильное влияние другие факторы (уровень производственных издержек, конъюнктура спроса, цены конкурентов и др.). Интерпретация моделей регрессии начинается со статистической оценки уравнения регрессии в целом и оценки входящего в модель факторного признака. Прежде всего, необходимо оценить коэффициенты регрессии. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если коэффициент регрессии при факторном признаке имеет знак «плюс», то с увеличением данного фактора результативный признак возрастает; если знак «минус», то с ростом значений этого факторного признака значения результативного признака уменьшаются. Если экономические процессы подсказывают, что факторный признак должен иметь положительное значение, а он имеет знак «минус», то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при вычислении. С целью расширения возможностей экономического анализа используются коэффициенты эластичности, определяемые по формуле:  , (86)где – среднее значение соответствующего факторного признака; – среднее значение результативного признака; a1 – коэффициент регрессии при соответствующем факторном признаке. Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1 %. Пример 4. Определим коэффициент эластичности по данным примера 73. 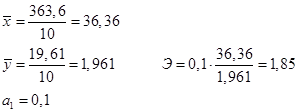 Таким образом, при увеличении загрузки мощности компьютера на 1 % время реакции соответственно увеличится на 1,85 %. Вопросы для самопроверки: 1. Что можно сказать о связи, если линейный коэффициент корреляции равен: а) нулю; б) единице; в) -0,15? 2. Если вы выявили сильную положительную корреляцию, говорит ли это о том, что большие значения факторного признака вызывают появление больших значений результативного? Если нет, какие еще возможны варианты? 3. Что представляют собой параметры «массив1» и «массив2» при расчете линейного коэффициента корреляции Пирсона в MS Excel? 4. Какие требования к исходным данным важно соблюдать, приступая к расчету коэффициента корреляции в MS Excel? 5. В чем состоят особенности применения регрессионного анализа? 6. Если результативный и факторный признак имеют тенденцию к стабильному росту, то какой аналитической функцией описывается взаимосвязь между ними? 7. Что характеризует коэффициент регрессии в уравнении связи и важно ли учитывать его знак? 8. Что показывает коэффициент эластичности? 9. Какой показатель используется для оценки тесноты связи между x и y при существовании между ними нелинейной зависимости? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания. Задание 1. Какой метод анализа – корреляционный или регрессионный – следует применить в каждой из описанных ниже ситуаций?
Задание 2. По данным авто.ru о предложении на продажу автомобиля с пробегом марки Volvo S60 c двигателем «турбодизель» определите, какой из показателей «срок эксплуатации» или «пробег» в большей степени оказывает влияние на цену продажи. Постройте уравнение регрессии между показателем «цена продажи» и наиболее сильно влияющим на него показателем. Интерпретируйте полученное значение коэффициента регрессии при факторном признаке.
Задание 3. Определите вид корреляционной зависимости, рассчитайте значение коэффициента корреляции, постройте уравнение регрессии между объемом реализованной продукции и балансовой прибылью 10 предприятий одной из отраслей промышленности. Интерпретируйте полученные значения показателей.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
