цйу. Документ Microsoft Word (2). Программа дисциплины Статистика
 Скачать 1.87 Mb. Скачать 1.87 Mb.
|
|
Базисные (по сравнению с 2007 г.): 2. Рассчитаем цепные (гр. 4) и базисные (гр. 5) темпы роста: Цепные (по сравнению с предшествующим годом): Базисные (по сравнению с 2007 годом): 3. Рассчитаем цепные (гр. 6) и базисные (гр. 7) темпы прироста: Цепные (по сравнению с предшествующим годом): Тпр08/07 = 133,33 % – 100 % = 33,33 % Тпр09/08 =63,75 % – 100 % = -36,25 % Тпр 10/09 =132,55 % – 100 % = 32,55 % Тпр 11/10 =129,59 % – 100 % = 29,59 % Базисные (по сравнению с 2007 годом): Тпр 08/07 = 133,33 % – 100 % = 33,33 % Тпр 09/07 =85,00 % – 100 % = -15,00 % Тпр 10/07 =112,67 % – 100 % = 12,67 % Тпр 11/07 =146,00 % – 100 % = 46,00 % 4. Рассчитаем абсолютное значение одного процента прироста (гр. 8): |%|2008 = у2007 * 0,01 =300,0 * 0,01 = 3,000 млрд долл. США |%|2009 = у 2008 * 0,01 =400,0 * 0,01 = 4,000 млрд долл. США |%|2010 = у 2009 * 0,01 =255,0 * 0,01 = 2,550 млрд долл. США |%|2011 = у 2010 * 0,01 =338,0 * 0,01 = 3,380 млрд долл. США 5. Рассчитаем среднегодовой объем экспорта РФ в страны дальнего зарубежья за 2007–2011 гг. Рассматриваемый ряд динамики является интервальным рядом с равноотстоящими уровнями, поэтому используем формулу средней арифметической простой: 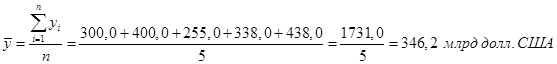 т.е. в среднем в период с 2007 по 2011 г. РФ ежегодно экспортировала в страны дальнего зарубежья товаров на сумму 346,2 млрд руб. 6. Определим средний абсолютный прирост объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. Он составит: Это означает, что в среднем за 2007–2011 гг. объем экспорта РФ в страны дальнего зарубежья ежегодно возрастал на 34,5 млрд долл. США. 7. Рассчитаем средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. Таким образом, в среднем объем экспорта РФ в страны дальнего зарубежья в период с 2007 по 2011 г. ежегодно возрастал в 1,0992 раза. 8. Найдем значение среднего темпа прироста. Поскольку средний темп роста объема экспорта РФ в страны дальнего зарубежья в 2007–2011 гг. составил 109,92 %, отсюда средний темп прироста будет равен: Соответственно, в течение 2007–20011 гг. объем экспорта РФ в страны дальнего зарубежья в среднем ежегодно возрастал на 9,92 %. Вопрос 3. Тенденция ряда динамики и методы ее выявления. Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Для выявления основной тенденции развития в статистике применяются две группы методов (рис. 38): 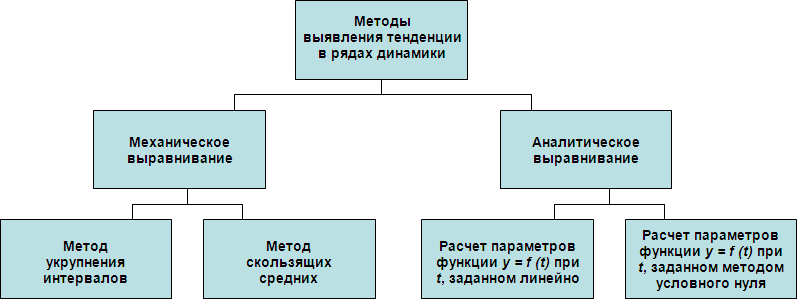 Рис. 38. Методы выявления тенденции в рядах динамики Аналитическое выравнивание основано на расчете теоретических значений уровня ряда по наиболее подходящей модели их изменения. Модель представляет собой уравнение функции, позволяющей получить значения уровней ряда на основании значений фактора времени y = f(t). График теоретических значений образует линию, проведенную между конкретными уровнями ряда таким образом, чтобы она отражала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний. Механическое выравнивание (сглаживание) уровней ряда динамики осуществляется с использованием фактических значений соседних уровней. В результате получается новый ряд динамики, в котором колебания уровней в значительной мере погашены и основная тенденция развития этого ряда проступает более наглядно. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни. Например, ряд недельных данных можно преобразовать в ряд помесячной динамики, ряд квартальных данных заменить годовыми уровнями. Уровни нового ряда могут быть получены путем суммирования уровней исходного ряда либо могут представлять средние значения, рассчитанные по соответствующим уровням. Метод скользящей средней. Выравнивание или сглаживание ряда динамики методом скользящих средних сводится к замене фактических уровней ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям, что способствует более четкому проявлению тенденции развития. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчете средних уровней они как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название – скользящая средняя. Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики нечетное. Нахождение скользящей средней по четному числу уровней ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимся в середине интервала сглаживания. Например, средняя, найденная для четырех первых уровней, относится к середине между вторым и третьим уровнями, средняя из значений показателя, стоящих в ряду динамики на втором, третьем, четвертом и пятом местах, придется на середину между третьим и четвертым уровнями, и так далее. Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. Для этого необходимо найти скользящие суммы, затем по этим суммам рассчитать скользящие средние нецентрированные и после этого произвести центрирование – последовательно найти средние арифметические значения из соседних нецентрированных скользящих средних. Пример 2. Покажем расчет скользящих средних за 3 и 4 месяца по данным, представленным в таблице 62. Таблица 62. Объем оказанных платных услуг населению региона за 2012 г.
В результате расчета трехуровневых скользящих средних получен новый ряд значений объема оказанных услуг (графа 3 табл. 62), представленный на рисунке 39 а). Поскольку рассчитанные трехуровневые средние значения возрастают, то ряд динамики объема оказанных платных услуг населению имеет общую тенденцию к росту. Тенденция к росту отчетливо видна также и на графике. 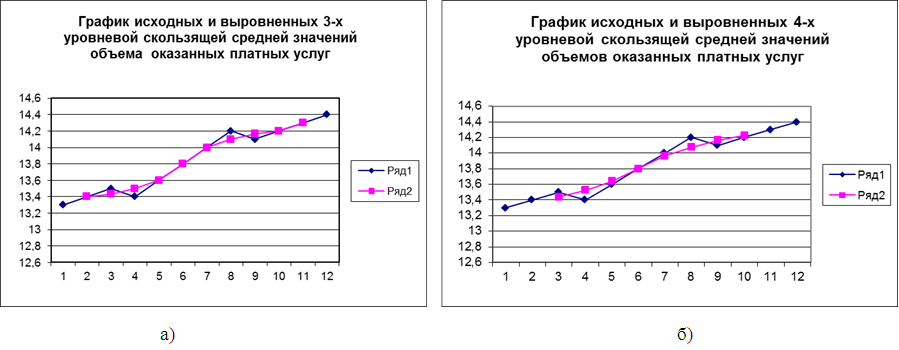 Рис. 39. Графики динамики исходных и выровненных 3- и 4-уровневой скользящими средними значений объема оказанных платных услуг населению региона по месяцам 2012 г. где Ряд 1 – исходные данные; Ряд 2 – значения соответствующих скользящих средних. Анализ значений четырехуровневых скользящих средних (графа 6 табл.62), изображенных на графике 39 б), также подтверждает наличие в ряду динамики объема оказанных платных услуг населению тенденции к росту. Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции. Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени: = f(t). При таком подходе изменение явления связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени. Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы разной степени, экспоненты, логистические кривые и другие виды. Полиномы имеют следующий вид: полином первой степени: полином второй степени: полином третьей степени: полином n-ой степени: Здесь a0; a1; a2; … an – параметры полиномов, t – условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, например, параметр a0 характеризует средние условия развития ряда динамики, параметр a1 – скорость роста, параметр a2 – ускорение роста, параметр а3 – изменение ускорения. Оценка параметров в моделях 87 находится методом наименьших квадратов. Как известно, суть его состоит в определении таких параметров (коэффициентов), при которых сумма квадратов отклонений расчетных значений уровней от фактических значений была бы минимальной. Таким образом, эти оценки находятся в результате минимизации выражения: где: yt – фактическое значение уровня ряда динамики; – расчетное значение; n – количество уровней в ряду динамики. Тогда система нормальных уравнений для оценивания параметров прямой 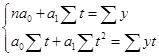 (89) (89)Для параболы второго порядка (yt = a0+ a1 t + a2 t2): 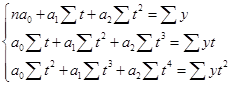 (90) (90)Закономерность, согласно которой изменяются значения уровней ряда динамики, в статистике принято называть трендом, а математическое выражение функции, описывающей это изменение – уравнением тренда. Так, например, рассчитав параметры прямой Для расчета параметров полиномов необходимо ввести в модель числовые значения для фактора времени t. Это можно сделать двумя способами. 1. Ввести фактор временилинейно, т.е. у первого уровня ряда t1 = 1, у второго t2 = 2, у третьего t3 = 3, у предпоследнего tn–1 = n – 1 и у последнего tn = n. 2. Другой подход заключается в обозначении фактора времени методом условного нуля. Для этого начало координат условно переносится в середину ряда динамики. Если в ряду нечетное количество уровней, то начало координат 0 совпадает с серединным уровнем ряда. Тогда для серединного уровня ряда ti будет равно 0, а у остальных уровнейti будет указываться со знаками «+» и «-», двигаясь в соответствующие стороны от 0 к крайним уровням ряда динамики. При четном числе уровней 0 попадает в интервал между серединными уровнями ряда. Строго следуя законам математики, серединным уровням следовало бы присвоить ti = -0,5 и ti = +0,5. Однако, пользуясь свойствами арифметической прогрессии и для упрощения числовых значений ti, серединным уровням присваивают ti= -1 (= -0,5 * 2) и ti= +1 (= 0,5 * 2), а для остальных уровней вводят ti c соответствующим знаком, сохраняя шаг прогрессии 2. Тогда, если до переноса начала координат ряд ti выглядел как 1, 2, 3, ..., n, то после переноса: · для нечетного числа уровней ряда ti = …; -3; -2; -1; 0; 1; 2; 3; · для четного числа уровней ряда ti = …; -5; -3; -1; 1; 3; 5. Следовательно, и все , у которых «р» - нечетное число, равны 0. Таким образом, все члены уравнений, содержащие с такими степенями, могут быть исключены. Системы нормальных уравнений теперь можно упростить. Для прямой при 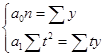 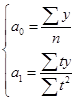 (91) (91)Для параболы второго порядка: 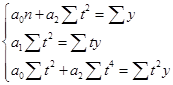 (92) (92)Решая системы (91) и (92), получим величины параметров соответствующих полиномов. Если в ряду динамики цепные абсолютные приросты примерно равны, то аналитическое выравнивание лучше проводить по модели прямой, если при расчете разностей между соседними цепными приростами (вторых разностей) получаются примерно одинаковые значения, то аналитическое выравнивание следует проводить по модели параболы. Пример 3. Определим основную тенденцию ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (табл. 63). Таблица 63. Исходные и расчетные данные аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (значения фактора времени t заданы методом условного нуля)
Для каждого уровня выравниваемого ряда динамики в графе 2 присваиваем обозначение фактора времени t методом условногонулятаким образом, чтобы 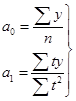 Затем в графах 3 и 4 проводим необходимые расчеты и находим: Отсюда: Уравнение прямой будет иметь вид: На основе этого уравнения находятся выровненные месячные уровни (графа 5 таблицы 63) путем подстановки в него соответствующих значений ti(из графы 2). Параметр а1 полученного уравнения показывает, что объем оказанных платных услуг населению региона в течение 2012 г. возрастал в среднем на 0,0535 млн руб. ежемесячно. Таким образом, величина параметра а1 в уравнении прямой показывает среднюю величину абсолютного прироста выровненного ряда динамики. Сумма уровней эмпирического ряда Результаты произведенного аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона и исходные данные отражены на рисунке 40. На этом рисунке Ряд 1 – исходные значения, а Ряд 2 – теоретические выровненные методом аналитического выравнивания значения, рассчитанные по уравнению тренда 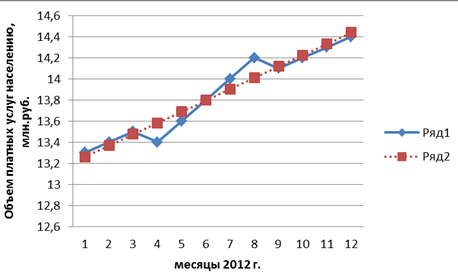 Рис. 40. Динамика объема оказанных платных услуг населению региона по месяцам 2012 г. Вопрос 4. Простейшие методы прогнозирования. Анализ динамики социально-экономических явлений, выявление и характеристика основной тенденции развития дают основание для прогнозирования – определения будущих размеров уровня экономического явления. Процесс прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой, а в прошлое – ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевают чаще всего перспективную экстраполяцию. К простейшим методам экстраполяции относятся: прогнозирование на основе среднего абсолютного прироста, прогнозирование на основе среднего темпа роста и экстраполяция на основе применения метода аналитического выравнивания. Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов). Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения прогнозного значения на k шагов вперед указанными методами необходимо использовать следующие формулы: Таблица 64. Формулы расчета прогнозных значений простейшими методами прогнозирования
Пример 4. По данным об объеме оказанных платных услуг населению региона (табл. 63) по месяцам 2012 г. построим помесячный прогноз на I квартал 2013 г. методом среднего абсолютного прироста и методом среднего темпа роста. Для наглядности расчетов представим начальные и конечные уровни, необходимые для расчета среднего абсолютного прироста и среднего темпа роста, в таблице 65. Таблица 65. Фрагмент ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (по данным табл.62)
Для получения прогнозных значений методом среднего абсолютного прироста: 1) определим средний абсолютный прирост: 2) по формуле 93 рассчитаем прогнозные значения для следующих трех периодов: 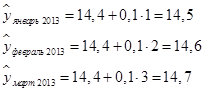 3) определим средний темп роста по формуле: 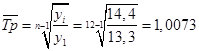 4) используя формулу 94, рассчитаем прогнозные значения для следующих трех периодов: 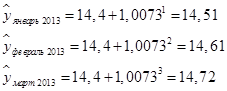 Для удобства сравнения объединим результаты прогнозирования в таблице 66. Таблица 66. Прогнозные значения объемов платных услуг населению региона по месяцам I квартала 2013 г. (млн руб.)
К недостаткам рассмотренных методов следует отнести то, что они учитывают лишь конечный и начальный уровни ряда, исключая влияние промежуточных уровней. Тем не менее методы среднего абсолютного прироста и среднего темпа роста имеют весьма широкую область применения, что объясняется простотой их вычисления. Наиболее распространенным методом прогнозирования является расчет прогнозных значений показателя на основе аналитического выражения тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения переменной времени (t). Как правило, для целей прогнозирования расчет параметров уравнения тренда осуществляют, вводя значения фактора времени (t) линейно. Пример 5. По данным о динамике объема оказанных населению платных услуг по месяцам 2012 г. (млн руб., табл. 67.) построим помесячный прогноз на 1 квартал 2013 г. методом экстраполяции тренда. Таблица 67. Таблица исходных и расчетных данных аналитического выравнивания ряда динамики объема оказанных платных услуг населению региона по месяцам 2012 г. (значения фактора времени t заданы линейно)
Построим линейную модель тренда вида: 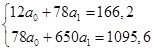 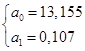 Следовательно, Для получения прогнозных значений методом аналитического выравнивания необходимо в полученную модель подставить значения фактора времени t для прогнозируемых месяцев. Продлевая ряд t, узнаем, что для января 2013 г. t = 13, для февраля 2013 г. t = 14, а для марта t = 15. Прогнозные значения представим в табл. 68. Таблица 68. Прогнозные значения объема платных услуг населению на I квартал 2013 г. (по месяцам, млн руб.)
Вопросы для самопроверки: 1. Что такое ряды динамики? Какие виды рядов динамики вы знаете? 2. Что означает несопоставимость уровней рядов динамики и из-за чего она возникает? 3. Что характеризует: абсолютный прирост, темп роста, темп прироста? В чем разница между этими показателями? 4. Какой показатель является обобщающим показателем абсолютной скорости изменения явления во времени? 5. Что такое тенденция ряда динамики? 6. Для чего применяют метод скользящих средних? В чем основные преимущества и недостатки его использования? 7. В чем состоят исходные предпосылки применения метода аналитического выравнивания? 8. Что такое тренд и уравнение тренда? 9. Какой прием используют для упрощения расчетов параметров уравнения тренда при аналитическом выравнивании ряда динамики? 10. Какие методы экстраполяции вам известны, как они реализуются? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания. Задание 1. Имеются следующие данные о размерах страховых выплат страховых организаций РФ за период 2005–2011 гг. (трлн руб.):
а) Рассчитайте значения индивидуальных аналитических показателей динамики. б) Рассчитайте значения среднего абсолютного прироста и среднего темпа роста. в) Рассчитайте прогнозные значения объема страховых выплат на 2012 и 2013 гг. методами среднего абсолютного прироста и среднего темпа роста и занесите их в соответствующие графы сводной таблицы, приведенной ниже:
Задание 2. По данным о динамике среднего размера вклада (депозита) физических лиц на рублевых счетах в Сбербанке РФ за 2005–2012 гг. (на начало года, тыс. руб.) произведите аналитическое выравнивание ряда и рассчитайте параметры линейного уравнения тренда. Для обозначения фактора времени при построении модели используйте метод условного нуля. Рассчитайте теоретические значения среднего размера вклада используя полученное уравнение тренда, и занесите их в соответствующую графу таблицы.
Задание 3. Вы решили изучить поквартальное количество посетителей своего ресторана, воспользовавшись методом анализа трендов. Линейный тренд описывается уравнением вида уt= 5423 + 408 * t, причем номер квартала начинается с единицы в I квартале 2009 г. и увеличивается на единицу для каждого последующего квартала. а) Найдите прогнозные значения для четырех кварталов 2013 г. б) Ваш стратегический бизнес-план развития ресторана включает проект значительного расширения бизнеса (количество посетителей ресторана должно достичь 60 000 за год). В каком году (в соответствии с вашим прогнозом) это должно произойти впервые? Подсказка: вычислите и сложите четыре прогнозных поквартальных значения, чтобы найти величину показателя за соответствующий год. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
