Вопросы по информатике. Программа это последовательность инструкций, предназначенных для выполнения компьютером
 Скачать 295.5 Kb. Скачать 295.5 Kb.
|
1 2
|
| 1 2 3 4 5 6 7 | public class Test { public static void main(String[] args){ double a = 20 + Math.random()*40; System.out.println(a); } } |
Как это работает?
Шаг №1: Диапазон [0;1) умножается на 40. Соответственно,
Нижняя граница: 0*40 = 0
Верхняя граница: 1*40 = 40
Получаем диапазон [0;40)
Шаг №2: К диапазону [0;40) прибавляем 20. Соответственно,
Нижняя граница: 0 + 20 = 20
Верхняя граница: 40 + 20 = 60
Получаем диапазон [20;60)
Если просто подставить в формулу, то получим:
( Math.random() * (60 - 20) ) + 20 => Math.random() * 40 + 20
№9 Форматный вывод. Форматная строка. Понятие и виды специфика-
торов формата. Форматирование целых чисел. Форматирование ве-
щественных чисел. Указание минимальной ширины поля. Примеры
Форматный вывод — вывод в различные потоки, значений различных типов, отформатированный по определенным правилам.
System.out.printf(“форматная строка“, список аргументов);
Спецификаторы форматного вывода начинаются с %
%a - шестнадцатеричное число с плавающей точкой
%b - булиан
%c - символ char
%e - научная нотация
%f - десятичное с плавающей точкой - float
%g - автоматически выбирает из double и float
%o - восьмеричное число. Автоматически переводит число в 8ую с/с.
%n - перевод строки
%s - строка
%x - шестнадцатеричное число. Автоматически переводит число в 16ую с/с.
%% - вставляет %
%d - десятичное число
#
n=10
System.out.printf(“6 + 4 = %d“, n); // 6+4=10



Спецификатор минимальной ширины – целое число, помещенное между символом % и кодом преобразования формата.
Спецификатор минимальной ширины дополняет вывод пробелами, обеспечивая заданную минимальную длину.
Если строка или число получаются короче, чем заданный минимум, то число выводится полностью. По умолчанию, дополнение осуществляется пробелами.

№ 10. Форматный вывод. Форматная строка. Понятие и виды специфика-
торов формата. Указание точности. Флаги формата. Использование
индекса аргументов. Примеры.
Чтобы дополнить число лидирующими нулями, нужно поместить 0 перед спецификатором ширины поля
System.out.printf ("%09d\n", x);
000001234
Спецификатор точности
может быть применен к спецификаторам формата %f, %e, %g и %s.
Спецификатор точности следует за спецификатором минимальной ширины поля (если таковой имеется) и состоит из точки с последующим целым числом. Спецификатор точности для данных с плавающей точкой (%f или %e) определяет количество отображаемых десятичных разрядов.
%10.4f – число в 10 символов шириной с 4 разрядами после запятой.
При использовании %g точность определяется количеством значащих десятичных разрядов.
Точность по умолчанию – 6 знаков после запятой
double x = 12345.6789;
System.out.printf ("%10.3f", x);
12345.678
Для строк спецификатор точности задает максимальную ширину поля. Если строка длиннее максимальной ширины, конечные символы усекаются.
Флаги формата
позволяют управлять различными аспектами преобразования.
Все флаги формата – одиночные символы, которые следуют за знаком % в спецификаторе формата.
| Флаг | Эффект |
| - | Выравнивание влево |
| 0 | Вывод дополняется нулями вместо пробелов |
| Пробел | Положительным числам предшествует пробел |
| + | Положительным числам предшествует знак + |
| , | Числовые значения, включающие групповые разделители |
| ( | Отрицательные числовые значения заключены в скобки |
По умолчанию весь вывод выравнивается вправо.
Для выравнивания по левому краю, нужно поставить знак минус после сразу после %.

12
Данные флаги работают со знаком числа:

Флаг запятая
При отображении больших чисел удобно использовать разделители групп. Например 1234567 читается легче в виде 1 234 567. Для добавления спецификаторов группирования служит флаг запятая.
System.out.printf ("%,.2f", 4356783497.34);
4 356 783 497.34
Использование индекса аргументов
Обычно все аргументы выводятся последовательно (то есть согласно порядку их добавления в команду). Но это можно изменить используя обращение к индексу аргумента.
Индекс аргумента следует за % в спецификаторе формата и имеет вид n$, где n – индекс нужного аргумента, начиная с 1.
System.out.printf("%3$d %1$d %2$d", 10, 20, 30);
Вывод: 30, 10, 20
Преимущество индексирования аргументов: повторное использование аргумента.
System.out.printf("%1$d в шестнадцатеричном формате это %1$X%n", 255);
255 в шестнадцатеричном формате это FF
№ 11. Логический тип данных. Логические операции. Замыкающие логические операции и их особенности. Применение замыкающих логических операций. Законы де Моргана
boolean — логический тип данных. Может принимать значения true и false (правда и лож)
Логические операции:
& – конъюнкция (И, логическое умножение)
| – дизъюнкция (ИЛИ)
^ – исключающее ИЛИ (XOR)
|| – замыкающее ИЛИ
&& – замыкающее И
! – отрицание
== – равно
!= – не равно
Замыкающиеся логические операции пренебрегают значением второго оператора, если можно дать ответ по значению первого.
# true | x = true
false & x = false
boolean a = del != 0 && n / del > 10;
Если del = 0, то вторая часть выражения не будет вычисляться
Закон Де Моргана
| Выражение | Отрицание выражения | Отрицание выражения |
| a && b | !(a && b) | !a || !b |
| a || b | !(a || b) | !a && !b |
№ 12. Разветвляющиеся алгоритмы. Полная и неполная формы ветвления.
Условный оператор и его особенности. Пример программы с блок-
схемой. Условные оператор и логические переменные. Тернарный
оператор. Примеры.
Условный оператор позволяет производить выбор для различных исходов выполнения условия:
#
if (условие){
Если условие верно
} else {
Иначе выполнится другой код
}
Если после условия выполняется только один оператор, то можно убрать фигурные скобки!
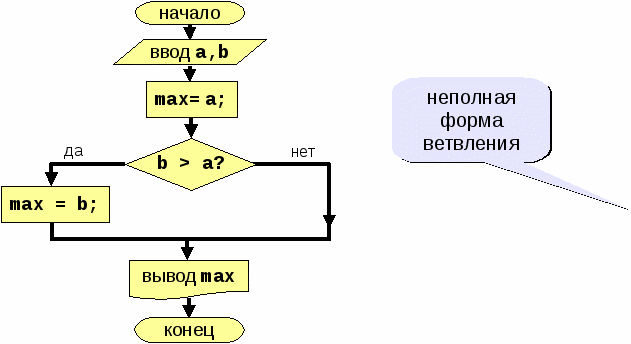
# if (b>a)
max=b
Пример неполного ветвление
Так же в конструкцию if можно класть бульку
cat = true;
if (cat){
Если cat = true
} esle {
Если cat = false
}
Тернарный оператор — позволяет заменить конструкцию if else.
# <Логическое выражение> ? <если истина, то выполнится это выражение> :
<если лож, то это выражение>
#
System.out.println((a < b) ? a : b);
Тернарный оператор обязательно должен что-то возвращать (равняться переменной) или выводить значение операции на экран
№13. Сложные условия. Порядок выполнения логических операций. При-
мер программы с блок-схемой
Сложное условие — это условие состоящие из нескольких простых условий, связанных с помощью логической операции
Логические операции
! - не (отрицание)
&& - и (логическое умножение)
|| - или (логическое сложение)
# Нужно найти сотрудника с возрастом от 25 до 45 лет
if (year >=25 && year <=45)
System.out.println(“Сотрудник подходит“);
else System.out.println(“Сотрудник не подходит“);
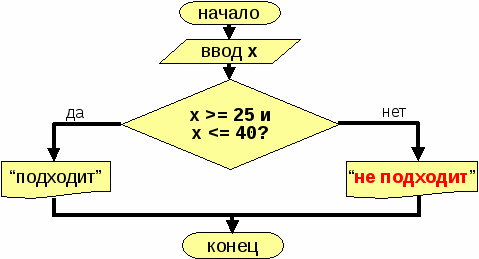
Порядок выполнения сложных условий
1) ! - не
2) <, <=, >, >=
3) ==, !=
4) &&
5) ||
№14. Оператор выбора. Порядок выполнения оператора выбора. Особенности оператора выбора. Вложенные операторы выбора.
Оператор выбора swift — является простым способом выбора из большого числа команд
switch (выражение){
case значение1:
//команды1;
break;
case значение2:
//команды2;
break;
case значение3: case значение4:
//команды3;
break;
default: выполняется если другие значения не сработали
}
Команда break прерывает выполнение swift после отработки блока кода
Пример
int i = in.nextInt(); // положительное
switch(i) {
case 0:
case 1:
case 2:
case 3:
System.out.println("i меньше 4");
break;
case 4:
case 5:
case 6:
case 7:
System.out.println("i меньше 8");
break;
default:
System.out.println ("i равно или больше 8");
Swift может быть вложен в другой Swift.
Данные оператор хорошо подходит для случаев, когда нужно проверить выражение на равенство
№15. Цикл с известным числом шагов и его особенности. Пример программы с блок-схемой. Приемы накопления суммы и произведения, комбинация приемов. Рекуррентные соотношения. Переменные-флаги.
Переменные-счетчики
Цикл с известным числом шагов необходим для более компактной записи повторяющихся фрагментов программы.
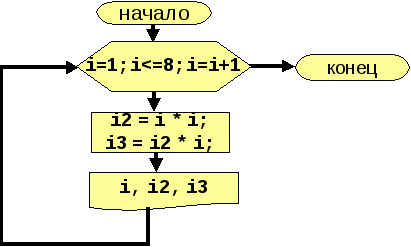
# Нужно вывести квадраты и кубы чисел от 1 до 8
for (i = 1; i <= 8; i++){
System.out.printf("i = %d", i);
System.out.printf("i*i = %d", i*i);
System.out.printf("i*i*i = %d", i*i*i);
}
Иногда в программе с циклом нужно найти сумму определенной последовательности чисел
# Например 1!+2!+3!+… + n!
Int p=1; sum = 0;
for (i = 1; i <= n; i++){
p = p*i; //Нахождения факториала следующего числа
sum = sum + p; //Сложение факториалов
}
В данном примере происходит одновременное накопление суммы и произведения
Примечание в цикле может быть несколько переменных или условий или различный шаг.
#Пример цикл который выводит четные числа последовательности
for (i = 0; i <= n; i +=2){
System.out.printf("i = %d", i);
}
Рекуррентное соотношение — это цикл, который периодически обращается и использует одну или несколько переменных последовательности
#
x=1;
for (i = 1; i <= 5; i++){
x = 2 — x*x;
}
Переменные флаги — это бульки, которые находясь в цикле позволяют опередить выполняется ли то или иное условие.
#Пример: узнать является ли последовательность упорядоченной по возрастанию
int x, x2;
boolean isGrowing = true; //изначальное положение - правда
x = in.nextInt(); //считываем новое целое число
for (int i = 2; i <= 10; i++) {
x2 = x;
x = in.nextInt(); //х — следующее число
isGrowing = isGrowing && (x > x2); //Если последовательность все еще правдивая, тогда узнаем является ли следующее число больше чем предыдущее. Если последовательность уже не равна правде, то сравнение не будет производиться
}
#Переменные счетчики — нужны для того, чтобы узнать, какое количество раз выполняется то или иное условие.
#Пример узнать сколько чисел из определенного диапазона делится на 3
for (int i=1; i <= 10; i++){
if (i%3 ==0) {
d++;
}
// int g = (i % 3 == 0) ? d++ : d;
}
№16. Цикл с условием и его особенности. Пример программы с блок-схемой.
Вычисления с заданной точностью. Цикл с постусловием и его особенности.
Цикл с условием необходим в том случае, когда мы не знаем сколько раз необходимо провести ту или иную операцию для получения необходимого результата.
#
While(условие){
тело цикла
}
Например нам нужно выводить все числа до тех пор пока не а меньше b.
Int a = 4, b =6;
while (a
a++
Цикл While может служить заменой для for
Так же циклы можно использовать для произведения вычислений последовательностей с заданной точностью
Пример: Синус можно разложить в так называемый ряд Тейлора:
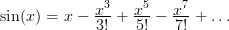
Чем большее количество членов ряда будет просуммировано, тем точнее будет вычислен синус. Пусть требуется вычислить до 5-го знака после запятой. То есть приемлемая погрешность 10-5 .
double eps = 1e-5; //необходимая точность
double x = in.nextDouble(); //считываем новое числа
double p = x, s = x;
int n = 2;
while (Math.abs(p) > eps) { //происходит сравнение числа с нобходимой точностью
p = -p * x * x / (n * (n + 1));
s = s + p;
n += 2;
}
System.out.printf("sin(x) = %f", s);
Цикл с постусловием — это цикл, проверка в котором выполняется в конце цикла.
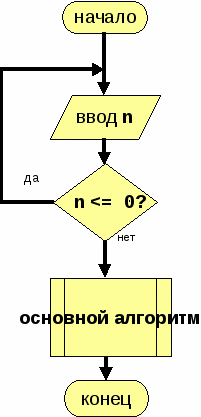
do{
System.out.printf("Введите положительное числа");
n = in.nextInt();
} while ( n <= 0); //условия продолжения цикла
... { основной алгоритм }
№17. Вложенные циклы. Примеры. Операторы перехода и их особенности:
break, continue,return. Варианты использования оператора break. Использование break в качестве оператора безусловного перехода.
В теле любого оператора цикла могут находиться другие операторы цикла. При этом цикл, содержащий в себе другой, называют внешним, а цикл, находящийся в теле первого — внутренним (вложенным). Правила организации внешнего и внутреннего циклов такие же, как и для простого цикла.
Пример:
for (int i = 1; i <= 5; i++) {
for (int j = 1; j <= 10; j++) {
System.out.print("*");
}
System.out.println();
}
Оператор break служит для завершения выполнения блока кода. (одного цикла). Так же break может служить как замена оператору goto:

Оператор continue применяется, когда в текущей итерации цикла необходимо пропустить все команды до конца тела цикла.
При этом сам цикл не прерывается, условия продолжения или выхода вычисляются обычным образом.
В циклах while и do-while оператор continue вызывает передачу управления управляющему условному выражению цикла.
В цикле for управление передается вначале итерационной части цикла for, а потом условному выражению

Вывод:

Return — завершает выполнение метода и возвращает значение.
№18. Применение циклов. Аналитическое и точное решение. Численные
методы, их достоинства и недостатки. Метод дихотомии для решения
уравнения и его программная реализация. Особенности метода.
Типы решения:
Аналитическое — это точный метод, в котором для решения используется конкретная формула.
Графический метод и численные методы — приближенное решение
Идея численного метода заключается в последовательном уточнении решения при помощи некоторого алгоритма.
Плюсы:
1) Можно найти хоть какое-то решение
2) Можно оценить ошибку (найти решение с заданной точность)
Минусы:
1) Нельзя найти точное решение
2) Невозможного исследовать решение при изменении параметров
3) Нет универсального метода.
Метод дихотомии — заключается в делении объекта исследования по полам с целью нахождения ответа.
Пример: в телефонном справочнике нужно найти человека с фамилией начинающейся на Р.
1) Открываем на середине справочник.
2) Проверяем с какой стороны находятся фамилии на букву Р.
3) Если справа, то берем правую сторону и вновь выполняем проверку
4) Если слева, то берем левую сторону и вновь выполняем проверку
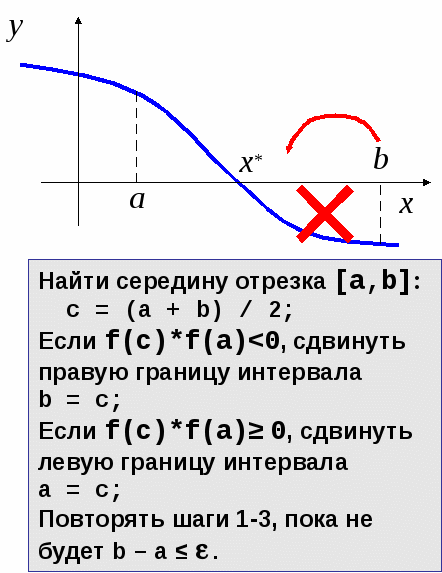
Программный пример
Дано уравнение
double a = 0, b = 10, c, eps = 1e-7;
int n = 0;
while (b - a > eps) { //Цикл работает до тех пор пока разность Левой и Правой границы > заданной разности
c = (a + b) / 2; //нахождение середины отрезка
if ((a*a + a - 6) * (c*c + c - 6) < 0) //Если произведение Ответа уравнения с параметрами с левой границы на произведение Ответа уравнения с середины отрезка < 0
b = c; //то смещаем левую границу
else
a = c; //Иначе смещаем правую границу
n++;
}
printf("x = %.16f, n = %d",(a + b ) / 2, n);
№19. Применение циклов. Аналитическое и точное решение. Численные
методы, их достоинства и недостатки. Численные методы вычисле-
ния площади криволинейной трапеции. Программная реализация од-
ного из методов.
Данный метод необходим для без интегрального вычисления площади криволинейной трапеции.
Вычислить её площадь можно разбив эту трапецию на участки и «заложив» эти участки прямоугольниками или трапеции. Далее нужно вычислить площади всех фигур лежащих внутри трапеции и просуммировать их.
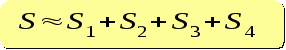
Пример: метод трапеции
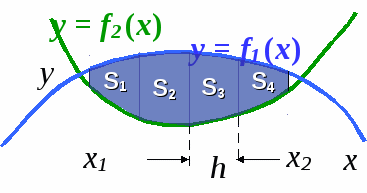
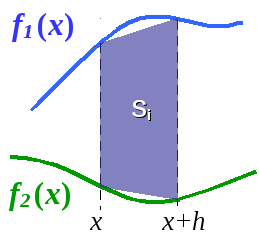
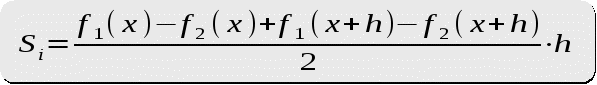
Формула для нахождения площади трапеции
for ( x = x1; x < x2; x += h ) //Цикл работает до тех пор пока левая граница не приблизится к правой
S += f1(x) – f2(x) +
f1(x+h) – f2(x+h);
S *= h/2 //Нахождение площади трапеции
Модифицированная версия алгоритма
for ( x = x1; x < x2; x += h ) //Цикл работает до тех пор пока левая граница не приблизится к правой
S =( f1(x1) - f2(x1) //Формула для нахождения средней линии трапеции
+ f1(x2) - f2(x2) )/2.;
for ( x = x1+h; x < x2; x += h ) //покоординатное умножение средней линии на высоту трапеции дает более точный результат
S += f1(x) – f2(x);
S *= h;
№20. Применение циклов. Аналитическое и точное решение. Численные
методы, их достоинства и недостатки. Численный метод вычисления
длины кривой и его программная реализация.
Численный метод для вычисления длины кривой нужен для приближенного и упрощенного вычисления длины кривой. Без использования интегралов
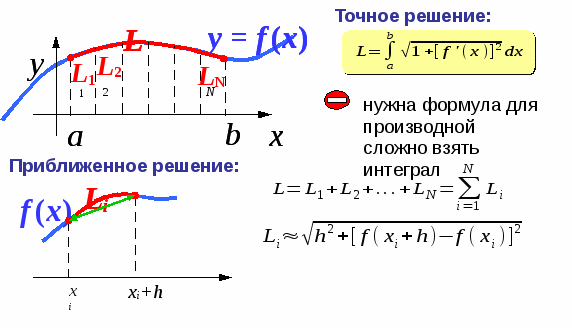
Численный метод для нахождения длины кривой, так же как и численный метод нахождения площади трапеции. Находит искомое значение из сумм значений полученный на различных интервалах.
Пример: Дана кривая y=x2. Найти длину кривой на отрезке от 0 до 4.
double a = 0, b = 4;
double x, dy, h = 1e-6;
double h2 = h * h;
double L = 0;
for (x = a; x < b; x += h) {
dy = (x + h)*(x + h) - x * x; // dy — правая точка отрезка. X — начальная точка; h — смещение по отрезку !НУЖНО ПОВТОРИТЬ
L += Math.sqrt(h*h+ dy * dy); //нахождение длины отрезка
}
System.out.printf("L = %.16f", L);
1) В данном алгоритме мы находим правую точку отрезка.
2) Вычисляем длину отрезка
3) Суммируем полученную длину с суммой уже имеющихся длин
4) Берем следующий отрезок и возвращаемся к шагу 1.
21. Статические методы. Понятие процедурной декомпозиции. Примеры
методов. Виды методов. Определение статического метода: составные части метода. Вызов статического метода. Статические методы, не возвращающие значения. Примеры.
Статические методы — позволяют избавить программный код от многократного повтора. И позволяют разложить код по разным функциональным блокам.
Процедурная декомпозиция — это представление программы в виде совокупности вызывающих друг друга подпрограмм.
Примеры статических методов — встроенные методы в java.
Например: Math.abs(); Math.random()
Методы могу возвращать и не возвращать данные.
public static void sum (int x, int y) { //Сначала описывается сигнатура метода
int z = x + y;
System.out.println(z);
}
void говорит о том, что данный метод не возвращает данные.
Int x и int y — входящие в метод параметры
22. Статические методы. Глобальные и локальные переменные. Формальные и фактические параметры. Статические методы, возвращающие значения, и их особенности. Логические методы. Примеры.
void говорит о том, что данный метод не возвращает данные.
Int x и int y — входящие в метод параметры. Формальные параметры
public static int sum (int x, int y) {
int z = x + y;
return z;
}
Данный метод будет возвращающим и вернет значение типа int
Метод может возвращать только одно значение!
Переменные объявленные внутри метода являются локальными и недоступны в других частях программы.
Для вызова статического метода необходимо написать его название и в скобках ввести входные данные:
#
public static int sum (int x, int y) { // x,y — формальные переменные
int z = x + y;
return z;
}
public static void main () {
x = nextInt();
y = nextInt();
System.out.println( sum(x,y) ); //вызовет метод sum и выведет его значение на экран x,y — фактические переменные
}
Логические методы — это методы которые на некоторый вопрос возвращают значение: true, false
Пример
//Функция для определения является ли число простым или нет
public static boolean isPrime ( int N )
{
int count = 0, i;
for (i = 2; i*i <= N; i++)
if (N % i == 0) count ++;
return (count == 0);
}
public statiс void main(String[] args)
{
int N;
N = in.nextInt();
if ( isPrime( N ) )
System.out.printf ("%d - простое число", N);
else System.out.println ("%d - составное число", N);
}
23. Сигнатура метода. Перегрузка методов. Примеры.
Перегрузка методов и операторов — это использование одного метода или оператора для разных целей:
Пример
public statiс void main(String[] args)
{
int a = 2, b = 3, c;
String r = «cat», h = «white»
c = a + b;
String f = r + « » + h;
}
В первом случае оператор + используется для суммирования двух целых чисел.
Во втором случае используется перегруженный метод оператора +. И он служит для СКЛЕЙКИ двух строк.
Итог: один метод/оператор — несколько предназначений
Сигнатура метода – совокупность его имени и набора формальных параметров.
Java позволяет создавать несколько методов с одинаковыми именами, но разными сигнатурами.
Создание метода с тем же именем, но с другим набором параметров называется перегрузкой.
Какой из перегруженных методов должен выполняться при вызове, Java определяет на основе фактических параметров.
Пример из презентации:

24. Использование класса Scanner для чтения данных из консоли, файла
и строки. Понятие лексемы. Процедура чтения данных из файла.
Методы класса Scanner. Примеры.
Scanner — класс, который умеет производить форматный ввод.
Данный класс может читать данный с клавиатуры и из файла.
Scanner in = new Scanner("10 99,88 сканирование это просто"); // in -это объект класса Scanner
int a = in.nextInt(); // 10
double b = in.nextDouble(); // 99.88
String s = in.next(); // "сканирование"
Так же класс Scanner может производить чтение данных заданного типа:
in.nextX(); / in- обращение к классу nextX — вызывает чтение данных нужного формата. Вместо X — нужно подставить необходимый формат данных.
Например Int, Double и т. д.
Чтение из файла:
Для начала нужно подключить пакет java.io.File; - Он позволяет работать с классом File.
Пример:
import java.io.File; //подключение чтения из файла
import java.io.FileNotFoundException; //обработчик ошибок
import java.util.Scanner; //Сканер
public class ScannFile2 {
public static void main(String[] args) throws FileNotFoundException {
File file = new File ("in.txt"); //Подключение нового файла
Scanner in= new Scanner(file, "cp1251"); // чтение данных из этого файла
}
throws FileNotFoundException - генерирует исключение ввода
Лексема — это порция входных данных, которую читает Scanner (обычно разделенная пробелом)
25. Класс PrintWriter. Методы класса PrintWriter. Примеры.
PrintWriter — класс, который применяется для записи файла.
Для данного класса так же нужно подключать пакет обработки файлов и обработчик ошибок.
import java.io.*;
public class Main {
public static void main(String[] args)
throws IOException {
PrintWriter out = new PrintWriter("out.txt"); //Создание тектового файла
out.print ("2 3,4 5 6 7,4 9,1 10,5"); //Запись данных в поток
out.close(); //Закрытие потока
}
}
Методы PrintWriter
| Метод | Описание |
| void close() | Закрывает поток. Последующие попытки записи генерируют исключения IOException. |
| void print(тип x) | Записывает значение x в выходной поток |
| void println(тип x) | Записывает значение x и перевод строки в выходной поток |
| void printf(“форматная строка”, список_аргументов) | Записывает в выходной поток отформатированную строку |
№ 26. Преобразование типов. Виды преобразования типов. Условия выпол-
нения неявного преобразования типов. Условия выполнения явного
преобразования типов. Общая форма явного преобразования. При-
меры. Виды приведений типов.
Преобразование типов — это переход от одного типа данных к другому.
Преобразование типов бывает явным и не явным.
Неявное преобразование — выполняется если типы данных сходны и величина исходного типа меньше величины целевого типа.
Пример:
long a = 5;
a = a + «A» + 32; //Сложение типа long с char и int. «При сложении типа char берется код нужного числа»
System.out.println( «a = » +a); // Сложение строки и числа.
Явное преобразование — целенаправленное преобразование одного типа к другому.
Пример:
int a =3;
byte r = (byte) a; //Команда byte говорит о том, что программист хочет осознанно преобразовать значение типа int к значению byte.
1) Если целевой тип меньше исходного, то происходит сужение типа.
2) Если вещественное значение приводят к целому, то происходит усечение.
Int к short — сужение
float к int — усечение
Виды приведения типов:
тождественное (преобразование типа к самому себе)
расширение примитивного типа
сужение примитивного типа
расширение объектного типа
сужение объектного типа
преобразование к строке
запрещенные преобразования
№ 27. Преобразование типов. Тождественное преобразование, расширение
простого типа. Возможные расширения простых типов. Искажения
при расширении простого типа. Примеры.
Тождественное преобразование — это преобразование типа в самого себя.
Обычно служит для уточнения той или иной операции.

В данном случае тождественное преобразование используется для упрощения чтения исходного кода.
(flat) во второй строчке кода дает быстро понять о том, какие данные необходимо получить.
Расширение простого типа — это переход от менее емкого типа к более емкому.
Данный тип перехода безопасный и не ведет к потере данных.
Пример переход от byte (1 бит) к int (4 бита) :
byte a = 3;
int b = a;
При переводе целых типов данных к вещественным возможны искажения. Поскольку у дробных типов для хранения целой части числа отведено меньшее количество разрядов.



№ 28. Преобразование типов. Сужения простого типа. Возможные виды
сужения простого типа. Алгоритм сужения дробного типа до цело-
численного. Примеры.
Сужение простого типа — это переход от более емкого типа к узкому. При сужение типов отбрасываются старшие биты, поэтому можно потерять данные.
Пример сужения простого типа

Сужение дробного типа до целочисленного происходит при явном переходе к типу данных вроде long и int.
Для дробных типов (float и double) сужение происходит по-своему. Если попытаться такое число привести к целочисленному типу — у него будет отброшена дробная часть.
public static void main(String[] args) {
double d = 2.7;
long x = (int) d;
System.out.println(x);
}
Вывод в консоль: 2
№ 29. Битовые операции. Битовые логические операции. Битовые маски и
их использование. Примеры.
Битовые операции — это операции, которые производятся с битовыми значениями чисел.
В java битовые операции могут применяться к целочисленным типам данных.
Битовые логические операции:
- инверсия
& - побитовое и
| - побитовое или
^ - xor (исключающее или)
» - сдвиг в право
>>> - сдвиг в право с заполнением нулями (без учета знака)
« - сдвиг в лево
Битовые маски служат для случаев, когда необходимо выделить определенные биты или цифры числа.
Лучше всего для создания битовой маски подходит операция И &. Так как она обнуляет все значения исходного числа, которые придется сравнивать с нулевыми значениями битовой маски.
Маска: обнуляются все биты, которые в маске равны «0».
Задача: обнулить 1, 3 и 5 биты числа, оставив остальные без изменения.


В данной операции произойдет побитовое сравнение числа n с битовой маской.
№ 30. Битовые операции. Битовые сдвиги: логический, циклический, ариф-
метический. Примеры
Битовые сдвиги передвигают (копируют) значение битов в соседние биты по направлению сдвига.
При логическом сдвиге значение последнего бита по направлению сдвига теряется (оно копируется в знак переноса). А первый бит приобретает значение нуля.

N = n << 1;
n = n >>> 1; - операции логического сдвига
Логический сдвиг в право — может заменить операцию * 2
Логический сдвиг в лево — заменяет операцию / 2
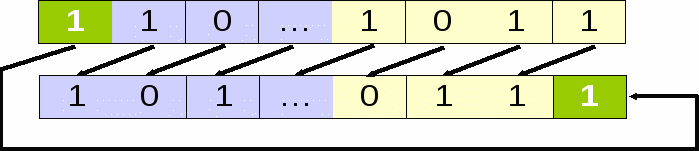
Циклический сдвиг — это сдвиг, при котором сдвигаемое значение (из знака переноса) переходит на новое свободное место. В JAVA данный тип сдвига не реализован
Арифметический сдвиг — это сдвиг, при котором не теряется знаковый (первый бит)
n = n » 1;

