Виртуальные демонстрации явления молекулярной физики. Программа Физика в картинках
 Скачать 354.43 Kb. Скачать 354.43 Kb.
|
|
Содержание Введение 2 1. Программа виртуальных демонстраций 4 1.1 Компьютерная программа «Физика в картинках» 4 1.2 Метод Монте Карло 5 2. Виртуальные демонстрации явления и процессов молекулярной физики 10 2.1 Виртуальная демонстрация явления диффузии 10 2.2 Виртуальная демонстрация броуновского движения 13 Заключение 19 Список использованных источников 20 ВведениеАктуальность дипломной работы. В настоящее время количество компьютерных программ, предназначенных для изучения физики, исчисляется десятками. Эти программы уже можно классифицировать в зависимости от вида их использования на уроках: обучающие программы; демонстрационные программы; компьютерные модели; компьютерные лаборатории; лабораторные работы; пакеты задач; контролирующие программы; компьютерные дидактические материалы. Важнейшим компонентом профессионально-методической подготовки учителя физики выступает практическая и экспериментальная подготовка студента, которая осуществляется на лабораторных занятиях. Соотнесение содержания и формы учебного эксперимента с современными научными представлениями постоянно обсуждается в научно-методической литературе, включая учебные пособия с разработкой тех или иных лабораторных занятий. Однако организационная сторона затрагивается редко, хотя играет отнюдь не второстепенную роль. Недостаточно исследованы возможности практических и лабораторных занятий по физике для осуществления профессионализации обучения студентов, улучшения их экспериментальной и общей подготовки. Таким образом, актуальность исследования обусловлена противоречиями между: преобразованиями в информационной культуре современного общества и требованиями к уровню самостоятельности личности; характером сложившихся форм организации, методов учебного процесса и необходимостью повышения уровня компетентности выпускника вуза; традиционным уровнем подготовки будущего учителя и современными потребностями школы, общества в высокоинтеллектуальном учителе. Цель дипломной работы является углубление знаний по рассматриваемой теме, исследование виртуальной демонстрации диффузии в том числе броуновского движения. Исследовать метод Монте Карло. Задачи дипломной работы: Рассмотреть и систематизировать материал по теме; Проверить на практике опыты. Объектом дипломного исследования являются процессы диффузии в металлах, виртуальная демонстрация явления диффузии Структура работы. Работа состоит из введения, двух глав, заключения и списка использованных источников. 1. Программа виртуальных демонстраций1.1 Компьютерная программа «Физика в картинках»  «Физика в картинках» – образовательный компьютерный курс. Это интегрированная база знаний в области физики. Курс включает справочник интерактивных моделей, имеет приятный интерактивный графический интерфейс, обеспечивает широкие возможности для более интенсивного обучения и привлечения студентов. В компьютерной программе "Физика в картинках" содержатся и проводятся демонстрации опытов с одновременно строящимися графиками, прилагаются пояснения процессов и явлений. Этот подход в компьютерной программе применяется ко всем основным темам школьного курса физики, что позволяет быстрее и качественней объяснить учебный материал, повышает наглядность и доступность обучения, даёт возможность демонстрировать неоднократно явления и процессы как в дискретном, так и в анимационном режимах. Можно просматривать изучаемые явления одновременно со строящимися графиками, менять в программе параметры факторов, создающих явления. Это позволяет разносторонне демонстрировать ход опытов, а учащимся глубже осваивать учебный материал. Использование этой программы эффективно на этапах закрепления и повторения учебного материала как в индивидуальном, так и в групповом обучении В настоящее время это одна из самых лучших программ по физике по научности, наглядности и компоновке учебного материала, которую можно применять на уроках параллельно с демонстрационным экспериментом После изучения какой-либо темы имеет смысл воспользоваться весьма содержательными вопросами и задачами, которые тут же можно вызвать на экран монитора. 1.2 Метод Монте КарлоДатой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «The Monte Carlo method». Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В СССР первые статьи о методе Монте-Карло были опубликованы в 1955-1956 гг. Любопытно, что теоретическая основа метода была известна давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т.е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин (ЭВМ) этот метод не мог найти сколько-нибудь широкого применения, ибо моделировать случайные величины вручную - очень трудоемкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ. Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом. Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. В действительности конкретное осуществление случайного процесса складывается каждый раз по-иному; так же и в результате статистического моделирования мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса. Что она может нам дать? Сама по себе ничего, так же как, скажем, один случай излечения больного с помощью какого-либо лекарства. Другое дело, если таких реализаций получено много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки могут быть получены любые интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т.д. При моделировании случайных явлений методом Монте-Карло мы пользуемся самой случайностью как аппаратом исследования, заставляем ее «работать на нас». Нередко такой прием оказывается проще, чем попытки построить аналитическую модель. Для сложных операций, в которых участвует большое число элементов (машин, людей, организаций, подсобных средств), в которых случайные факторы сложно переплетены, где процесс - явно немарковскпй, метод статистического моделирования, как правило, оказывается проще аналитического (а нередко бывает и единственно возможным). В сущности, методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета. Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен. Пусть, например, по какой-то цели производится три независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания. Элементарный расчет дает нам вероятность хотя бы одного попадания равной 1 - (1/2)3 = 7/8. Ту же задачу можно решить и «розыгрышем», статистическим моделированием. Вместо «трех выстрелов» будем бросать «три монеты», считая, скажем, герб - за попадание, решку - за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень-очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности. Ну, что же? Применить такой прием мог бы разве человек, вовсе не знающий теории вероятностей, тем не менее, в принципе, он возможен. Метод Монте-Карло- это численный метод решения математических задач при помощи моделирования случайных величин. Две особенности метода Монте-Карло Первая особенность метода - простая структура вычислительного алгоритма. Вторая особенность метода - погрешность вычислений, как правило, пропорциональна D/N2, где D - некоторая постоянная, N - число испытаний. Отсюда видно, что для того, чтобы уменьшить погрешность в 10 раз (иначе говоря, чтобы получить в ответе еще один верный десятичный знак), нужно увеличить N (т. е. объем работы) в 100 раз. Ясно, что добиться высокой точности таким путем невозможно. Поэтому обычно говорят, что метод Монте-Карло особенно эффективен при решении тех задач, в которых результат нужен с небольшой точностью (5-10%). Способ применения метода Монте-Карло по идее довольно прост. Чтобы получить искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей, следует: 1. Построить график или таблицу интегральной функции распределения на основе ряда чисел, отражающего исследуемый процесс (а не на основе ряда случайных чисел), причем значения случайной переменной процесса откладываются по оси абсцисс (х), а значения вероятности (от 0 до 1) - по оси ординат (у). 2.С помощью генератора случайных чисел выбрать случайное десятичное число в пределах от 0 до 1 (с требуемым числом разрядов). 3. Провести горизонтальную прямую от точки на оси ординат соответствующей выбранному случайному числу, до пересечения с кривой распределения вероятностей. 4.Опустить из этой точки пересечения перпендикуляр на ось абсцисс. 5. Записать полученное значение х. Далее оно принимается как выборочное значение. б. Повторить шаги 2-5 для всех требуемых случайных переменных, следуя тому порядку, в котором они были записаны. В задачах исследования операций метод Монте-Карло применяется в трех основных ролях: 1) при моделировании сложных, комплексных операций, где присутствует много взаимодействующих случайных факторов; 2) при проверке применимости более простых, аналитических методов и выяснении условий их применимости; 3) в целях выработки поправок к аналитическим формулам типа «эмпирических формул» в технике. Основным недостатком аналитических моделей является то, что они неизбежно требуют каких-то допущений, в частности, о «марковости» процесса. Приемлемость этих допущений далеко не всегда может быть оценена без контрольных расчетов, а производятся они методом Монте-Карло. Образно говоря, метод Монте-Карло в задачах исследования операций играет роль своеобразного ОТК. Статистические модели не требуют серьезных допущений и упрощений. В принципе, в статистическую модель «лезет» что угодно - любые законы распределения, любая сложность системы, множественность ее состояний. Главный же недостаток статистических моделей - их громоздкость и трудоемкость. Огромное число реализации, необходимое для нахождения искомых параметров с приемлемой точностью, требует большого расхода машинного времени. Кроме того, результаты статистического моделирования гораздо труднее осмыслить, чем расчеты по аналитическим моделям, и соответственно труднее оптимизировать решение (его приходится «нащупывать» вслепую). Правильное сочетание аналитических и статистических методов в исследовании операций - дело искусства, чутья и опыта исследователя. Нередко аналитическими методами удается описать какие-то «подсистемы», выделяемые в большой системе, а затем из таких моделей, как из «кирпичиков», строить здание большой, сложной модели. 2. Виртуальные демонстрации явления и процессов молекулярной физики2.1 Виртуальная демонстрация явления диффузииМоделью вещества, состоящего из постоянно движущихся молекул, объясняются некоторые физические явления. К примеру, диффузия — проникновение молекул одного вещества в молекулы другого. Рассмотрим данное явление подробнее. Начнем с газообразных тел. Представьте, что вы сидите за уроками в своей комнате и вдруг почувствовали вкусный запах с кухни. Почему это произошло? Блюдо, которое готовится к обеду, состоит из большого числа молекул, которые все время движутся и сталкиваются: мясо, масло, специи. При нагревании отдельные молекулы отделились от остальных, смешавшись с молекулами воздуха и стали перемещаться по квартире. Это явление уже упоминавшейся диффузии — взаимное проникновение молекул разных веществ. Диффузия может происходить в жидкостях и даже в твердых телах, но только значительно медленнее. Другой вопрос: почему же запахи не доносятся до нас мгновенно? Мы уже упоминали о беспрерывном и хаотичном движении молекул воздуха. таким образом, молекулы постоянно сталкиваются, меняют свое направление, и беспорядочно перемещаясь, разлетаются по помещению. Рассмотрим опыт, который покажет нам, что молекулы, из которых состоят тела, находятся в беспорядочном движении и в жидких телах (рисунок 1).  Рисунок 1. Иллюстрация опыта с водой и медным купоросом. Для начала нальем в стакан раствор медного купороса темно-голубого цвета (часто используется как бытовой антисептик). Затем аккуратно нальем в этот же стакан воды. Вначале между жидкостями будет видна резкая граница, но со временем она будет размываться. Через 2-3 недели граница исчезнет совсем: процесс диффузии завершится. Если рассмотреть данный процесс на молекулярном уровне (рисунок 2), то прекрасно видно, что молекулы воды и медного купороса на границе раздела этих двух жидкостей начинают меняться местами, а со временем жидкость в стакане и вовсе станет однородной. 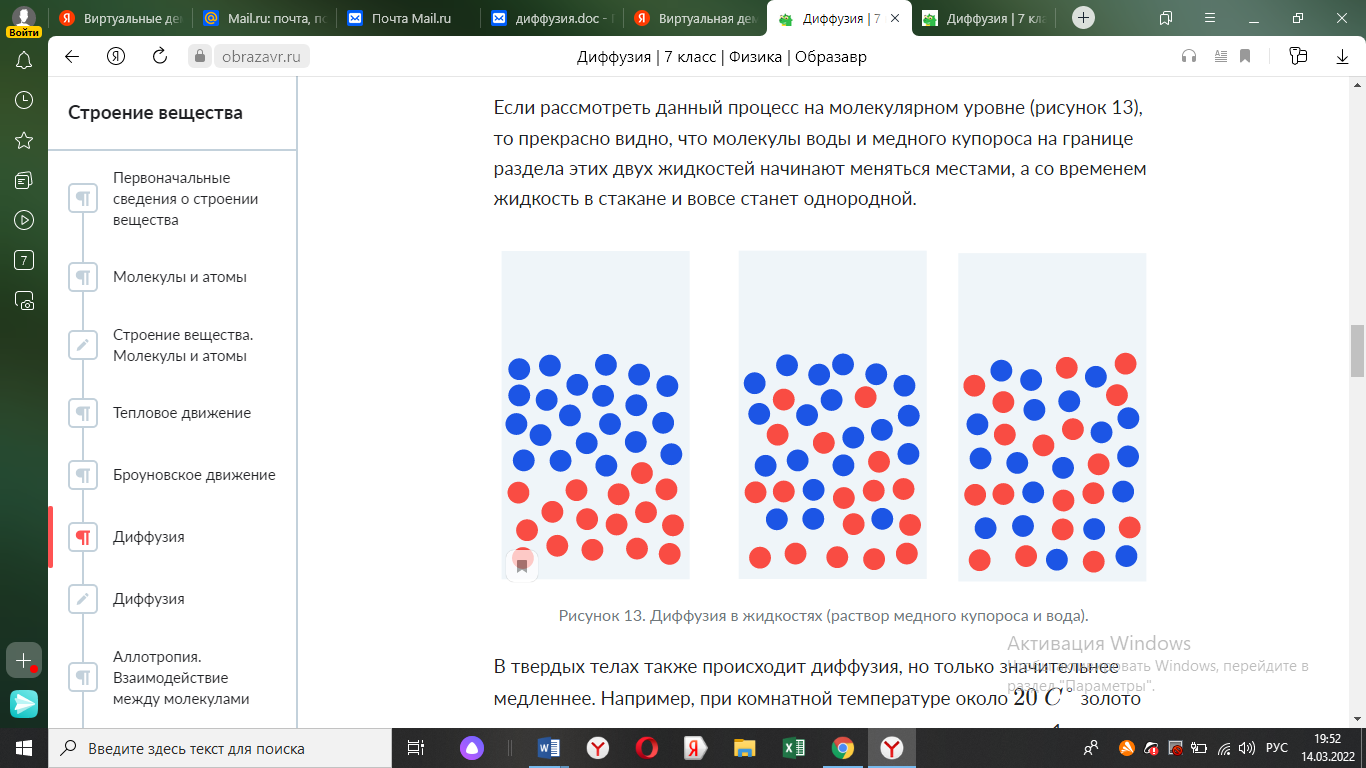 Рисунок 2. Диффузия в жидкостях (раствор медного купороса и вода). В твердых телах также происходит диффузия, но только значительнее медленнее. Например, при комнатной температуре около 20 \space C \degree20 C° золото и свинец взаимно проникнут друг в друга на расстояние около 1 мм только через 4-5 лет (рисунок 3). 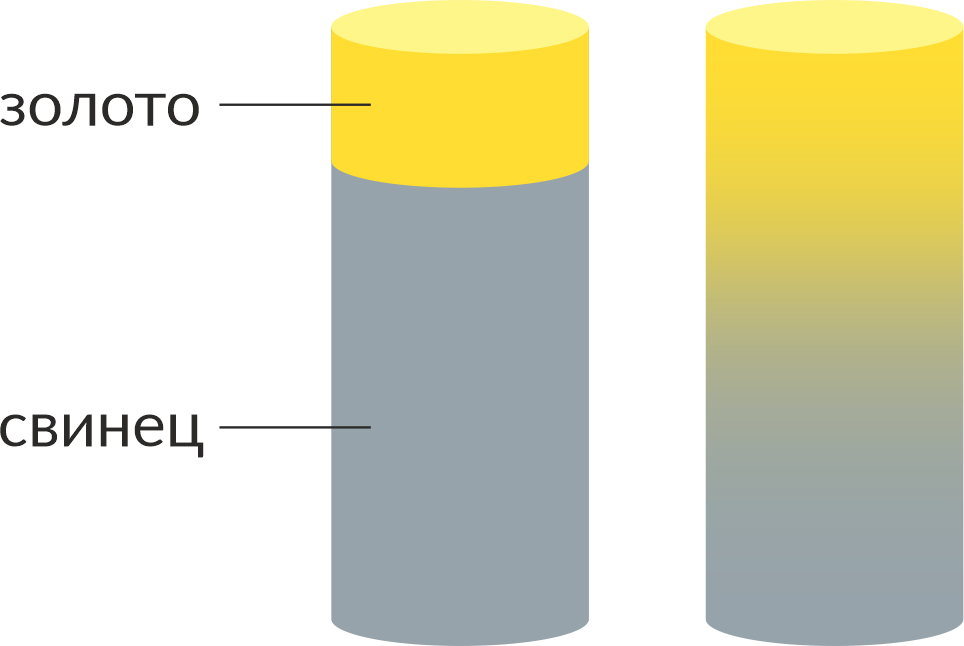 Рисунок 3. Диффузия в твердых телах (золото и свинец). Как мы уже говорили, явление диффузии объясняется непрерывным хаотичным движением молекул, в процессе которого молекулы одного вещества проникают в межмолекулярные промежутки другого. Процесс диффузии напрямую зависит от температуры, т.к. с увеличением температуры увеличивается скорость движения молекул. Процесс диффузии окружает нас как в повседневной жизни, так и в природе. Зачем мы завариваем чай в кипятке, ведь потом нужно ждать, пока он остынет? Почему не разогреть воду только до комфортной температуры? Ответ — чтобы ускорить процесс диффузии. В кипятке диффузия между молекулами чая, сахара и воды будет происходить намного быстрее, и чай заварится быстрее и лучше. В промышленности диффузия широко используется в технике при сварке деталей, склеивании. В природе благодаря диффузии поддерживается однородный состав атмосферного воздуха рядом с поверхностью Земли, а диффузия солей в почве позволяет растениям получать нормальное питание. 2.2 Виртуальная демонстрация броуновского движенияВ газете «1 сентября» Физика №16/08 опубликована статья «Броуновское движение «глазами» цифрового микроскопа». В ней автор рассказывает об опыте, преподавательский коллектив которой при изучении броуновского движения пользуется комплексом современного оборудования, в состав которого входят компьютер, микроскоп со встроенной цифровой камерой, интерактивная доска и мультимедийный проектор (или телевизор). В качестве микрочастиц для эксперимента используются минеральные частицы, содержащиеся в молоке, они примерно одного размера, порядка 1-2 мкм. Для приготовления препарата потребуется несколько капель молока, которые растворяют в воде, и переносят пипеткой в кювету глубиной 0,1 мм из обычного предметного стекла. (Такую кювету можно сделать следующим образом: две половинки покровного стекла толщиной 0,1 мм наклеиваются теплым парафином на предметное стекло на некотором расстоянии друг от друга. Промежуток заливается эмульсией и закрывается сверху покровным стеклом. Края кюветы парафинируются. См. рис.4). 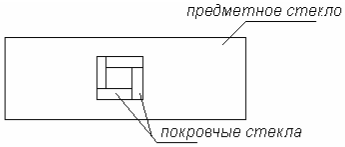 Рисунок 4. Кювета Современное оборудование (описанное выше) позволяет определять, как размер самой частицы, так и ее среднее перемещение за определенное время в абсолютном выражении. Изображение движущихся броуновских частиц выводятся на экран монитора и на интерактивную доску. Для проведения эксперимента необходимо два человека: один с помощью винта тонкой регулировки удерживает в фокусе ведомую броуновскую частицу (которая может перемещаться в глубь кюветы), наблюдая за ее движением на экране монитора, второй строит траекторию в виде ломаной линии на интерактивной доске. После чего на этой же доске результаты эксперимента обрабатываются в автоматическом режиме. Авторы некоторых учебников предлагают использовать для наблюдения броуновского движения явление дифракции и отражения света от системы малых частиц, опыт заключается в следующем. Приборы собирают по схеме, изображенной на рисунке 5. 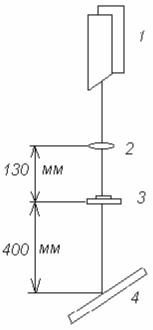 Рисунок 5. Схема установки, используемая для изучения броуновского движения Луч лазера 1, последовательно проходя через собирающую линзу 2 (фокусное расстояние линзы должно быть 6-8 см), предметное стекло 3, между которыми находится тонкий слой молока, попадает на экран 4. На экране наблюдают хаотическое движение темных и светлых областей, которое обусловлено броуновским движением частиц жира. (Особо следует подчеркнуть, что темные области нельзя рассматривать как область геометрической тени частиц жира. Эти области имеют дифракционную природу). Анализ компьютерных демонстраций броуновского движения Использование для наблюдения броуновского движения микроскопа с большим увеличением вызывает некоторые трудности из-за малой глубины резкости, применение современного оборудования (такого как интерактивная доска, микроскоп со встроенной цифровой камерой) оказывается слишком дорогим, поэтому натуральный физический эксперимент часто заменяют компьютерной моделью. Познакомимся более подробно с такими моделями броуновского движения и сравним две из них. Первая модель. Часть 1: Механика, механические колебания и волны, термодинамика и молекулярная физика». При выборе в меню раздела молекулярная физика  модели модели броуновское движение вниманию пользователя предоставляются три окна (рис.6.). броуновское движение вниманию пользователя предоставляются три окна (рис.6.).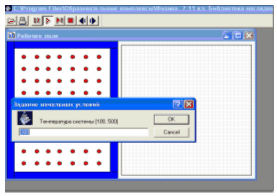 Рисунок 6. Пример 1 компьютерной модели броуновского движения В главном окне, имеется панель управления (в дальнейшем мы еще вернемся к кнопкам управления и опишем их более подробно). Окно «Рабочее поле» условно разделено на две части: слева изображается движение броуновской частицы (красного цвета) вследствие соударений с ней молекул вещества (зеленого цвета). При каждом новом запуске модели частица движется по новой траектории. При исследовании закономерностей броуновского движения в физическом эксперименте строится упрощенная траектория броуновской частицы в виде ломанной линии (ее модельный аналог выводится в правую часть окна), вершины которой отмечаются через равные промежутки времени. Значения координат вершин подвергаются статистической обработке. Окно «Задание начальных условий» предназначено для задания температуры Т системы. Следует отметить, что в данной компьютерной модели пользователь имеет возможность управлять только одним параметром – температурой системы, остальные характеристики частицы жестко определены. После задания начальных значений появляется еще одно дополнительное окно «Данные». Она располагается справа от «разлинованной» области и выглядит следующим образом (см. рис.7): 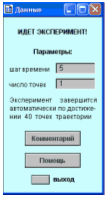 Рисунок 7. Окно «Данные» На панели располагаются две кнопки: «комментарий» и «помощь». Рассмотрим каждую из них. После нажатия кнопки «комментарий» вниманию обучающегося предоставляется: во-первых, определение броуновского движения, во-вторых, описываются процессы, которые должны происходить в окне «рабочее поле». При нажатии кнопки «помощь» пользователю дается пояснение по работе с моделью, а именно поясняется значение каждой из кнопок расположенных на панели управления в главном окне. 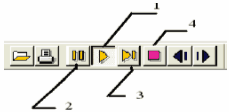 Рисунок 8. Панель управления системой После ввода начальных условий расчет модели приостановлен, чтобы пользователь мог рассмотреть общую картинку и принять решение по дальнейшим действиям. Для продолжения расчета следует нажать кнопку «Запуск» (1) на панели управления системой. При необходимости вновь приостановить расчет, следует нажать кнопку «Пауза» (2). Дальнейший расчет модели осуществляется при помощи кнопок «Запуск» (1) или «Шаг» (пошаговый расчет - 3). Для перезапуска модели следует нажать на панели управления сначала кнопку «Стоп» (4), затем – «Запуск» (1). Обратимся теперь ко второй модели броуновского движения. Для того, чтобы получить доступ к модели пользователю необходимо нажать на ссылку «Броуновское движение». Откроется окно, представленное на рис.9 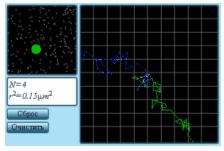 Рисунок 9. Пример 2 компьютерной модели броуновского движения Правила работы с этой моделью практически повторяют рассмотренную нами ранее модель. А именно, температура системы так же единственный параметр, который пользователь задает с клавиатуры. Несколько иначе авторы решили проблему оформления. В окне, расположенном несколько ниже изображения броуновского движения выводятся два значения, которые считаются автоматически. Так же имеются две кнопки: «Сброс» выполняющий функцию сброса параметров, и «Очистить» - очистка поля, на котором изображается траектория частицы. К сожалению, не удалось найти модель броуновского движения, в которой пользователь мог бы задавать с клавиатуры более одного параметра. В целом же можно сказать, что результаты, полученные по данным моделям, хорошо согласуются с теорией Эйнштейна-Смолуховского. ЗаключениеМожно сделать вывод, что работа обучающихся с компьютерными моделями чрезвычайно полезна, так как обучающиеся могут ставить многочисленные виртуальные опыты и даже проводить небольшие исследования. Но у виртуальной лабораторной работы есть и неоспоримые преимущества, так как она позволяет проводить компьютерные лабораторные эксперименты по физике для случаев, когда постановка реального эксперимента затруднена или необходимо мгновенно осуществлять обработку полученных результатов. Я представила вам небольшой перечень виртуальных образовательных ресурсов. Хочется отметить, что компьютерные лабораторные установки в виртуальных лабораториях, как правило, представляет собой компьютерную модель реальной экспериментальной установки. Выполнение экспериментальных исследований представляет собой непосредственный аналог эксперимента на реальной физической установке. Подведя итог всему вышесказанному можно сказать, что виртуальные лаборатории, можно использовать как на уроке, так и при самостоятельной подготовке к занятиям, они позволяют глубже понять законы физики и проникнуть в суть физических явлений. Нельзя забывать, что в большинстве случаев это четко запрограммированный процесс. Список использованных источников1. Кошкин И.И, Ширкевич М.Г. Справочник по элементарной физике. - М.: Наука, 2010. 2. Трофимова Т.И Курс физики. - М.: Высшая школа, 201. 3. Яворский Б.М, Детлаф А.А Справочник по физике. - М.: Наука, 2015. 4. Френкель Я. И., Собр. избр. трудов, т. 3 — Кинетическая теория жидкостей, М. — Л., 2019 5. Гиршфельдер Дж., Кертисс Ч., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 2011 6. Шьюмон П., Диффузия в твердых телах, пер. с англ., М., 2016 7. Франк-Каменецкий Диффузия А., Диффузия и теплопередача в химической кинетике, 2 изд., М., 2017 8. Булл Г., Физическая биохимия, пер. с англ., М., 2019 9. С. В. Богословский, Физические свойства газов и жидкостей, 2017 |
