Влияние антропогенных факторов на жизнь человека. Программа минимум а знать определения и обозначения следующих математических понятий, уметь приводить примеры, их иллюстрирующие
 Скачать 26.26 Kb. Скачать 26.26 Kb.
|
|
ПРОГРАММА МИНИМУМ а) знать определения и обозначения следующих математических понятий, уметь приводить примеры, их иллюстрирующие: частные производные функции двух переменных: -/фото/- (полное) приращение функции двух переменных: -/фото/- производная по направлению: -/фото/- градиент: -/фото/- точка максимума (минимума, экстремума) функции нескольких переменных: -/фото/- (обыкновенное) дифференциальное уравнение (д.у), его порядок, (частное) решение, интегральная кривая: (Обыкновенным) дифференциальным уравнением называется равенство вида F (x, y, y ′ … y (n)) = 0, связывающее между собой независимую переменную x, искомую функцию y (x) и ее производные y', y''… y (n) до производной некоторого порядка n включительно. Наивысший порядок производной (число n), входящей в дифференциальное уравнение, называется порядком этого уравнения. Решением (частным решением) уравнения на интервале I называется всякая функция, при подстановке которой в это уравнение вместе с ее производными, уравнение обращается в тождество относительно y=ϕ(x) при подстановке которой в это уравнение вместе с ее производными, уравнение обращается в тождество относительно x ∈ I. (В более широком смысле функцию, обладающую указанным свойством на любом открытом множестве, в практике также называют решением). Если решение дифференциального уравнения задается неявно уравнением Ф (х,у) = 0, то последнее равенство называют интегралом (частным интегралом) уравнения. График всякого решения дифференциального уравнения (или кривая на плоскости xy, заданная его интегралом) называется интегральной кривой этого уравнения. д.у. 1-го порядка, разрешенное относительно производной: общий вид начальное условие, задача Коши, общее решение: Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, имеет вид: y’ = f(x,y) Начальным условием для уравнения называется равенство вида Y (x 0) = y 0 Задача отыскания решения уравнения, удовлетворяющего заданному начальному условию, называется задачей Коши для этого уравнения. Геометрически задача Коши состоит в отыскании интегральной кривой уравнения, проходящей через заданную точку (x 0, y0) на плоскости xy. Функция y =ϕ (x, C) называется общим решением уравнения, если: 1) при любом допустимом значении параметра C она является решением этого уравнения; 2) любое частное решение уравнения (кроме, быть может, отдельных решений) представимо в виде y =ϕ (x, C0) при некотором значении C0 этого параметра (т.е. для любой точки (x 0, y0) ∈ D найдется такое значение C0, что y 0 =ϕ (x 0, C0)). Уравнение Φ (x, y, C) = 0, определяющее общее решение уравнения неявно, называют общим интегралом этого уравнения. д. у. n-го порядка, разрешенное относительно старшей производной: общий вид, начальные условия, задача Коши, общее решение: Дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной, имеет вид: Y (n)= f (x, y, y’,…,y(n-1)) Начальными условиями для уравнения называются n равенств вида y(x0) = y0, y’(x0) = y’0, y(n-1) (x0) = y0(n-1) Задача отыскания решения уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши для этого уравнения. Функция y=ϕ (x, C1, C2,…, Cn) называется общим решением уравнения, если: 1) при любых допустимых значениях параметров C1, C2,…, Cn она является решением этого уравнения; 2) любое его частное решение (кроме, быть может, отдельных решений) представимо в виде y=ϕ (x, C1, C2,…, Cn) при некоторых значениях параметров(т.е. для любой точки (x0, y0, y’0,…, y0(n-1)) ∈ D найдутся такие значения параметров C1, C2,…, Cn , что функция y=ϕ(x,C1, C2,…, Cn) будет удовлетворять начальным условиям). Уравнение Φ (x, C1, C2,…, Cn) = 0, определяющее общее решение уравнения неявно, называют общим интегралом этого уравнения. общий вид линейного д.у. (л.д.у.) n-го порядка (однородного и неоднородного): Линейным дифференциальным уравнением n-го порядка называется уравнение вида y (n)+a1 (x)y(n-1)+…+ a(n-1) (x)y’+ an (x)y = b(x), где коэффициенты a1(x), a2(x),…, an(x), а также правая часть предполагаются непрерывными функциями на некотором интервале I. Все решения этого уравнения определены на интервале I. Если b(x)= 0 ∀x ∈ I, то уравнение имеет вид y (n)+a1 (x)y(n-1) +…+ a(n-1) (x)y’+ an (x)y = 0 и называется однородным; в противном случае уравнение называется неоднородным. Линейно (не)зависимая система функций: Совокупность(система) из m функций y1(x), y2(x),…, ym(x) называется линейно зависимой на интервале I, если существуют числа α1, α2,…, αm , не все равные нулю и такие, что α1y1 + α2y2 +…+ αmym = 0 ∀x ∈ I; если же это равенство возможно только в случае α1 = α2 = … = αm = 0, то система называется линейно независимой. Две функции y1 и y2 (y2 ≠ 0), в частности, тогда и только тогда линейно зависимы, когда y1/ y2 = const. О 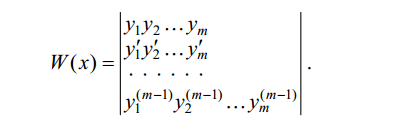 пределителем Вроньского (вронскианом) системы функций называется определитель Если хотя бы в одной точке x0 ∈ I имеем W(x0) ≠ 0, то система функций линейно независима на I. фундаментальная система решений однородного л.д.у (о.л.д.у): Всякая система из n линейно независимых решений о.л.д.у. n-го порядка называется фундаментальной системой решений этого уравнения. характеристическое уравнение для о.л.д.y. с постоянными коэффициентами: Многочлен n-й степени от переменной λ L(λ) = λn + a1λ(n-1) + … + a(n-1) λ + an, полученный из левой части уравнения путем замены производных yk искомой функции степенями λk, называется характеристическим многочленом, а алгебраическое уравнение n-й степени λn + a1λ(n-1) + … + a(n-1) λ + an = 0 – характеристическим уравнением для уравнения. б) знать следующие математические факты, формулы, формулировки теорем и утверждений: формула для вычисления дифференциала функции двух переменных: -/фото/- смысл направления и модуля градиента: -/фото/- необходимое условие экстремума дифференцируемой функции нескольких переменных: -/фото/- геометрический смысл задачи Коши для д.у. n-го порядка: Для дифференциального уравнения 2-го порядка (при n = 2) начальные условия имеют вид тройки чисел (x0, y0, y’0), и ставится задача отыскания решения y (x), для которого y(x0) = y0 и y’(x0) = y’0. Геометрически это означает выбор из совокупности интегральных кривых той, которая, во-первых, проходит через заданную точку плоскости (x0, y0), и, во-вторых, имеет в этой точке заданный угловой коэффициент касательной tg ϕ = y’0. свойства решений о.л.д.y.: Множество решений однородного линейного дифференциального уравнения (о.л.д.у.) обладает следующими свойствами: 1) если y1(x) и y2(x) – какие-нибудь два решения уравнения, то их сумма y1+ y2 также есть решение этого уравнения; 2) если y (x) – какое-нибудь решение уравнения и C– любое число, то их произведение Cy также есть решение этого уравнения. теорема о структуре общего решения о.л.д.у.: Если y1, y2, … , yn – какая-нибудь фундаментальная система решений уравнения, то его общее решение имеет вид: Y = C1y1 + C2y2 +…+ Cnyn, где C1 ,C2 … Cn– произвольные постоянные. теорема о характеристическом уравнении о.л.д.у. с постоянными коэффициентами: Функция eλx тогда и только тогда является решением дифференциального уравнения, когда λ есть корень (действительный или комплексный) соответствующего характеристического уравнения. свойства решений неоднородного л.д.у. (н.л.д.у.): Множество решений неоднородного линейного дифференциального уравнения (н.л.д.у.) обладает следующими свойствами: 1) если y1(x) – какое-нибудь решение неоднородного уравнения, а y0(x) – какое-нибудь решение соответствующего однородного уравнения, то их сумма y1 + y0 есть решение уравнения; 2) если y1(x) и y2(x) – какие-нибудь два решения уравнения, то их разность y1 - y2 есть решение соответствующего однородного уравнения. теорема о структуре общего решения н.л.д.y.: Общее решение н.л.д.у. равно сумме любого частного решения этого уравнения и общего решения, соответствующего о.л.д.у. В) уметь находить частные производные 1-го и 2-го порядков применять дифференциал для приближенного нахождения (полного) приращения функции двух переменных находить уравнения касательной плоскости и нормали поверхности F (x, y, z) = 0 исследовать на экстремум функцию двух переменных различать и решать д.у. 1-го порядка с разделяющимися переменными, однородные и линейные решать однородные и неоднородные л.д.у. 2-го порядка с постоянными коэффициентами (с правыми частями вида е αxР(х) и Мcosβx+Nsinβх, где P(x)-многочлен, М и N - const) |
