Применение Excel для решения статистических задач. Применение MS Excel для решения статистических задач. Программа обработки электронных таблиц ms excel мощная и достаточно простая в использовании программа, предназначенная для решения широкого круга плановоэкономических,
 Скачать 0.56 Mb.
|
Двухфакторный дисперсионный анализ без повторения.Представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности). Этот метод распространяется также на тесты для двух средних, такие как t-критерий.Корреляционный и ковариационный анализ.Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:  где: X, Y - множества значений случайных величин размерности m; M(X) - математическое ожидание случайной величины Х; M(Y) - математическое ожидание случайной величины Y. Как следует из формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0. Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель - коэффициент корреляции R, вычисляемый по формуле:  Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0. Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами: с помощью статистических функций КОВАР и КОРРЕЛ ; с помощью специальных инструментов статистического анализа. Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа. Инструмент анализа данных "Корреляция" Выберите в главном меню тему "Сервис" пункт "Анализ данных". Результатом выполнения этих действий будет появление диалогового окна "Анализ данных", содержащего список инструментов анализа. Выберите из списка "Инструменты анализа" пункт "Корреляция" и нажмите кнопку "ОК" (рис.1). Результатом будет появление окна диалога инструмента "Корреляция". Заполните поля диалогового окна, как показано на рис. 2 и нажмите кнопку "ОК". Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рис. 3.  Рис. 1 Список инструментов анализа (выбор пункта "Корреляция")  Рис.2. Заполнение окна диалога инструмента "Корреляция" 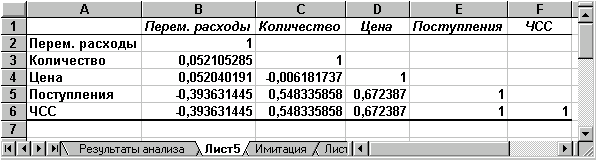 Рис. 3 Результаты корреляционного анализа Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой. Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей. [12] Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова,  . В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия и эксцесс. Для вычисления коэффициента асимметрии и эксцесса в EXCEL реализованы специальные статистические функции - СКОС () иЭКСЦЕСС(). [3] Инструмент анализа данных "Описательная статистика" Чем больше характеристик распределения случайной величины нам известно, тем точнее мы можем судить об описываемых ею процессов. Инструмент "Описательная статистика" автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных. Определим параметры описательной статистики. Для этого необходимо выполнить следующие шаги. Выберите в главном меню тему "Сервис" пункт "Анализ данных". Результатом выполнения этих действий будет появление диалогового окна "Анализ данных", содержащего список инструментов анализа. Выберите из списка "Инструменты анализа" пункт "Описательная статистика" и нажмите кнопку "ОК". Результатом будет появление окна диалога инструмента "Описательная статистика". Заполните поля диалогового окна, как показано на рис. 4 и нажмите кнопку "ОК". Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Выполнив операции форматирования, можно привести полученную ЭТ к более наглядному виду (рис.5).  Рис.4 . Заполнение полей диалогового окна "Описательная статистика" 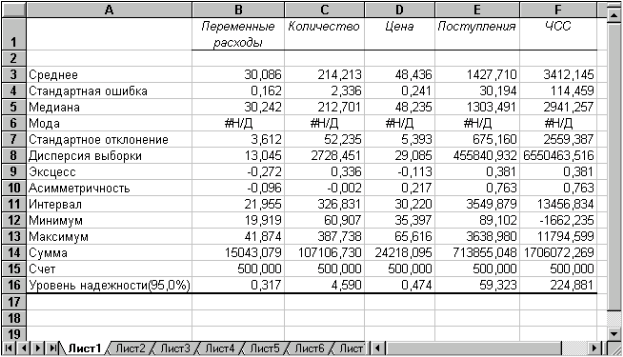 Рис.5. Описательная статистика для исследуемых переменных Вторая строка ЭТ содержит значения стандартных ошибок  для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М (Е) определено с погрешностью  . [1]Медиана - это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию. Мода - наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. В данном случае ППП EXCEL вернул сообщение об ошибке. Таким образом, вычисление моды не представляется возможным. Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь. [2] Асимметричность (коэффициент асимметрии или скоса - s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь. Для вычисления коэффициента асимметрии используется статистическая функция СКОС (). Формула для проверки значимости показателя эксцесса задается аналогичным образом. Числителем этой формулы будет функция ЭКСЦЕСС (), а знаменателем соотношение, реализованное средствами ППП EXCEL. Оставшиеся показатели описательной статистики представляют меньший интерес. Величина "Интервал" определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры "Счет"и "Сумма"представляют собой число значений в заданном интервале и их сумму соответственно. [3] Последняя характеристика "Уровень надежности" показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия.По умолчанию уровень надежности принят равным 95%. Анализ данных Дополнение "Анализ данных" содержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных. Вместе с тем, большинство из них требует осмысленного применения и соответствующей подготовки пользователя в области математической статистики. Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных. |