ПРОГРАММНОЕ СРЕДСТВО РЕАЛИЗАЦИИ АЛГОРИТМА «ФЛОЙ-ДА–УОРШЕЛА». Итог курсового проекта. Программное средство реализации алгоритма флойдауоршела
 Скачать 1.65 Mb.
|
1 Постановка задачиОписание предметной областиНа сегодняшний день информационные технологии очень глубоко проникли в повседневную жизнь. Почти каждый член развитого общества пользуется благами научного прогресса, которые облегчают человеческую жизнь, делают возможным быстрый обмен информацией и распространение ее в больших массах за малый срок. Благодаря этому технологическому рывку стало возможно существенное использование алгоритма Флойда–Уоршелла [1]. Алгоритм находит существенное применение, как и в частных компаниях, так и у обычных физических лиц, которые повседневно пользуется навигатором, такси и др. Например, существует карта города — её транспортная система это граф, соответственно присвоив каждому ребру некую стоимость, рассчитанную из пропускной способности и других важный параметров — реализуется возможность подвести попутчика по самому короткому/быстрому/дешевому пути. Для улучшения понимания алгоритма Флойда–Уоршелла разберем следующие определения: Граф – это средство для наглядного представление элементного состава и структуры связей (рисунок 1.1). 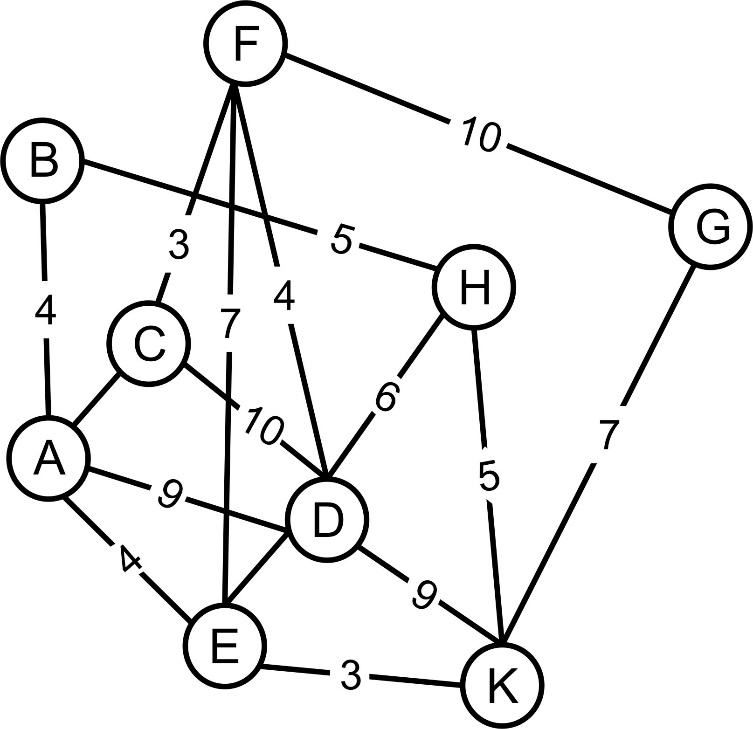 Рисунок 1.1 – Пример графа Вершины графа – это компоненты системы, изображаемые кругами, овалами, прямоугольниками и пр. Ребра – это линии, связывающие компоненты между собой. Графы могут быть как неориентированным (рисунок 1.2), т.е. вес ребра будет актуален как при передвижение из вершины А в вершину В, так и на оборот, или граф может быть ориентированы (рисунок 1.3), т.е. вес для ребер указан только в одном направлении. 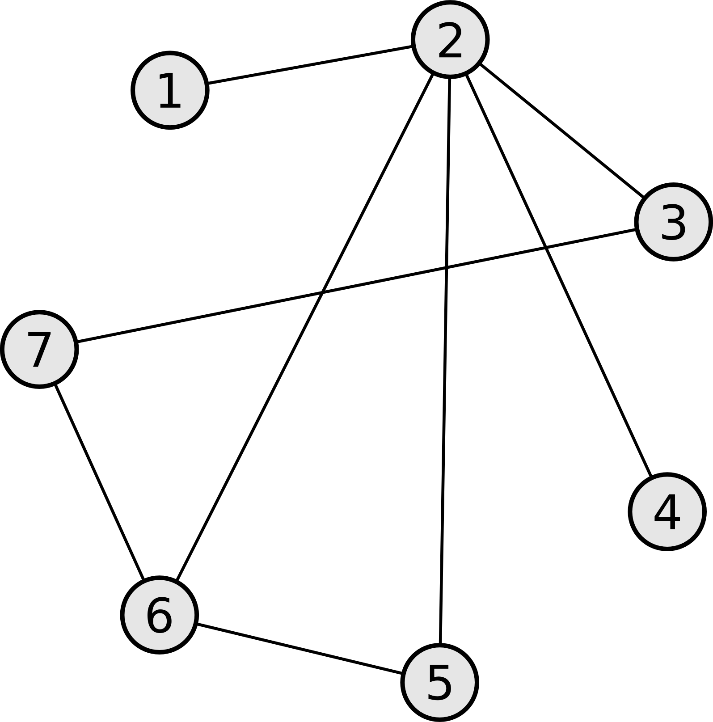 Рисунок 1.2 – Неориентированный граф 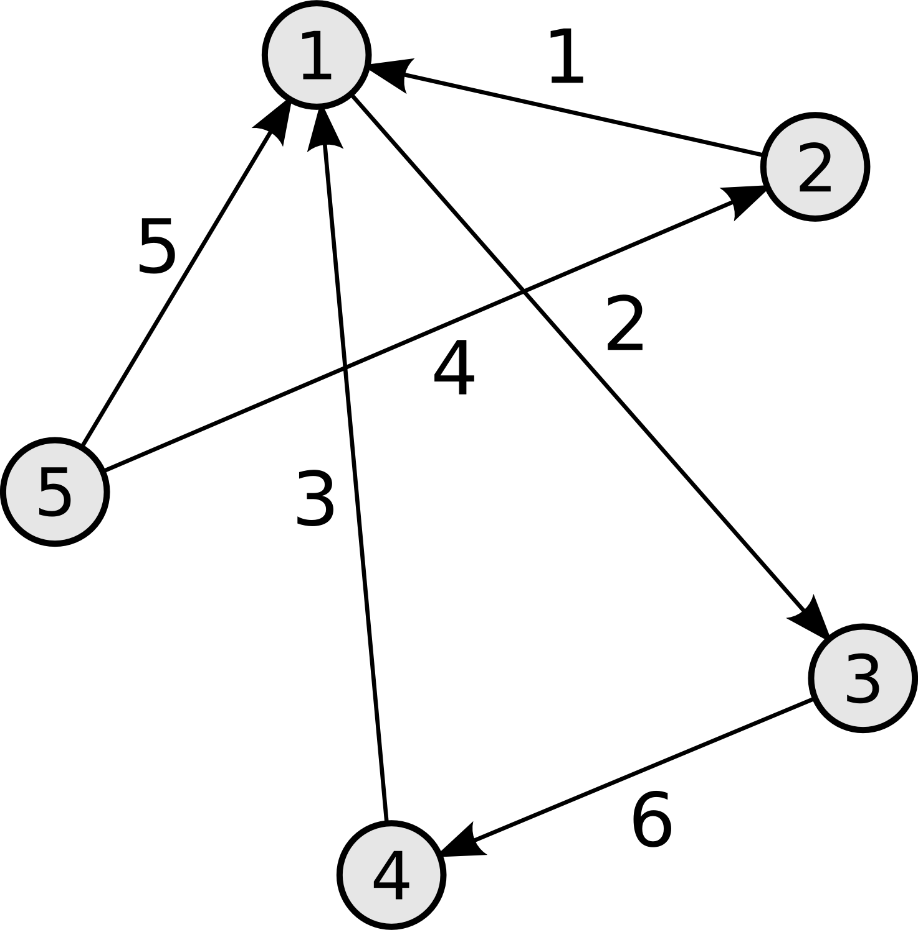 Рисунок 1.3 – Ориентированный граф Научный прогресс за последние сто лет привнес большое количество технологий, которые на сегодняшний день используются в транзитных отношениях. На сегодняшний день, специалист плохо ознакомленный с алгоритмами кратчайшего пути и другими инструментами для оптимизации транзитных перевозок, способен принести убытки как своей личной карьере, так и компании. На данный момент визуализация алгоритма Флойда–Уоршелла является актуальной, поскольку существует малое количество средств способных наглядно показать нахождения кратчайшего пути. Для нахождения кратчайшего путь при помощи алгоритма Флойда–Уоршелла выполняют следующие действия. Рассмотрим граф с вершинами {v1, v2… vn}. В графе существует путь рij от vi до vj, который проходит через множество вершин. Обозначим через  – длину кратчайшего пути из i в j, проходящего через вершины v1…vk-1. Расширим множество разрешенных вершин на одну: v1…vk. При этом возможны две ситуации. Ситуация 1: вершина vk не входит в кратчайший путь от i в j. Длина кратчайшего пути не изменится, соответственно  . Ситуация 2: вершина vk входит в кратчайший путь от i в j. Новый кратчайший путь разбит вершиной vk на два пути рik и рkj (кратчайшее расстояние от vi до vk и кратчайшее расстояние от vk до vj). Значит общая длина пути . Вершина vk в данных путях либо конечный, либо начальный элемент, в множество промежуточных она не входит, поэтому  . Для обоих рассмотренных случаев минимальный путь складывается из минимальных длин путей для предыдущих значений. Зная начальные значения при k=0 можно последовательно найти все остальные пути.  - минимальное расстояние от i до j проходящее через 0 вершин, другими словами это длина прямых соединений между i до j, которое известно с. |