Лабораторная №1, информатика, 1 курс. КП. Простые вычисления
 Скачать 75.76 Kb. Скачать 75.76 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра РАПС ОТЧЕТ по лабораторной работе №6 по дисциплине «Информатика» Тема: Простые вычисления
Санкт-Петербург Цель работы Освоить технику работы с математическим пакетом Matlab, а также научиться с его помощью проводить простые математические вычисления. Основные теоретические положения Matlab –это пакет прикладных программ, предназначенный для решения широкого спектра инженерных и научных задач любой сложности в любых отрослях. Ход работы 6.1 Я запустил Matlab, после чего ознакомился с его рабочей средой (рис1.) 6.2 В окно Command Window я ввел операцию «1+2» и нажал клавишу Enter, после чего на экране появился результат, который присваивается переменной «ans» (рис.2а). В окне Workspace можно посмотреть значение этой переменной, также так будут показаны значения всех переменных, которые я буду использовать при решении заданий (рис.2б) 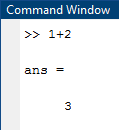 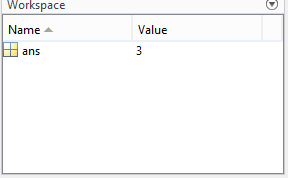 Рис.1а Рис.1б Чтобы изменить значение переменной «ans», я набрал в командной строке «ans/4.5», после чего на экране появился результат(рис.3а), который присваивается «ans», поэтому ее значение в окне Workspace также изменится (рис.3б) 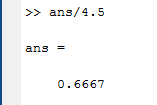 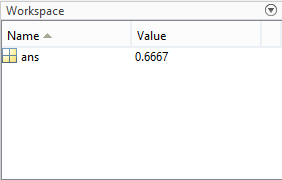 Рис.3а Рис.3б 6.3 Чтобы изменить формат ввода результатов вычислений я выбрал в меню «File» пункт «Preferences». Затем выбрал «short» в раскрывающемся списке» Numeric format» (Числовой формат)(рис.4). В окно Command Window я ввел операцию «100/3» и нажал клавишу Enter. 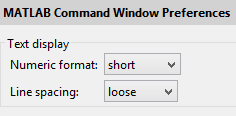 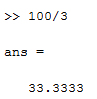 Рис.4 Задание 1 Условие: найти ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности кругового конуса, у которого высота вдвое меньше, чем длина образующей. Объем этого конуса равен 1. Основные геометрические формулы, используемые при расчете. Объем конуса: Vc= (1/3)∙ π∙r2∙h (1) Площадь боковой поверхности конуса: S = π∙r∙l(2) Соотношение в конусе между радиусом основания, высотой и длиной образующей: r2 + h2 = l2 (3) Площадь поверхности шара: S = 4∙π∙R2 (4) Объем шара: Vsh = (4/3)∙π∙R3 (5) Объем куба: Vkub = a3 (6) Решение: Обозначим объем конуса Vc=1, r - радиус основания конуса, l – длина образующей конуса l = 2*h (где h – высота конуса), Sbc – площадь боковой поверхности конуса, R – радиус шара, a – ребро куба, Vsh – объем шара, Vkub – объем куба . Используя формулу (3) и учитывая условие l = 2*h, я получил формулу h=r/√3. После чего из формулы (1) я выразил: 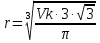 Затем я ввел эту формулу в командную строку, получив результат r=1,1826 (рис.5). Далее я вычислил l=(r∙2)/√3 и S по формуле (2). Получившиеся результаты можно увидеть на рис. 6. 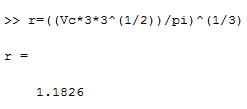 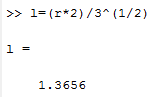 Рис.5 Рис.6 После чего по формуле выраженной из формулы (4) я вычислил радиус шара R (рис.7): 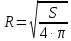 Далее я вычислил Vsh по формуле (5) (рис.8), после чего нашел искомое ребро 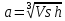 (рис.8) (рис.8)  Рис.7 Рис.8 Таким образом, ответ в задании 1: а = 1.0243. Задание 2 Условие: Вычислить стоимость поездки на автомобиле на дачу (туда и обратно). Исходными данными являются: расстояние (rast) до дачи (км); количество бензина (potr), которое потребляет автомобиль на 100 км пробега; цена одного литра бензина (cena). Основная формула, используемая при расчете: sum=2·potr/100·rast·cena (7) Решение: в командной строке я присваиваю значения переменным rast=95, potr=6,5 и cena=43 (рис. 9,10). Используя формулу (7), я вычисляю значение sum (рис.10)   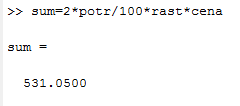 Рис.9 Рис.10 Рис.11 Таким образом, ответ в задании 2: sum = 531.05 Задание 3 Условие: вычислить величину дохода по вкладу. Процентная ставка (% годовых) и время хранения (дней) задаются. Решение: пусть sm – первоначальная величина вклада, p – процентная ставка, d – количество дней, на которое деньги кладут в банк, g – количество дней в году, а D – искомый доход по вкладу. В командной строке я присваиваю значения переменным sm = 15000, p = 13, d = 95. Формула для вычисления дохода по вкладу выглядит так: D=sum·pr·dn/(god·100). (8) Подставляю величины в формулу (8) и получаю значение D (рис.10) Таким образом, ответ в задании 3: D= 507.5342 Задание 4 Условие: Вычислить объем цилиндра. Заданы радиус основания r и высота цилиндра h. Основная формула, используемая при расчете: V=π·r2·h. (9) Решение: В командной строке я присваиваю значения переменным r = 4, h = 6. После чего считаю значение объема V по формуле (9) (рис.12) Таким образом, ответ в задании 4: V= 301.5929   Рис.12 Рис.12Использование элементарных функций В MATLABe есть различные тригонометрические, логарифмические и степенные функции, которые можно использовать при расчетах. Некоторые из них я применил ранее в задачах, однако более подробно расскажу в следующем примере (рис.13
Здесь для решения мне потребуются функции log для вычисления натурального логарифма, sqrt для выделения квадратного корня, а также тригонометрические функции sin, cos и tg. При введении всего примера в командную строку, получаю результат с использованием элементарных функций (рис.14)
Чтобы внести изменения в формулу, которую я ввел ранее, можно нажать на клавишу <↑>, которая вводит в командную последнюю введенную мною формулу. Благодаря этому я могу внести в нее изменения (рис.15).
Данная функция помогает сэкономить время, которое может потребоваться на перепечатывание всей формулы. Вывод MATLAB – это среда и язык технических расчетов, с помощью которого можно решать разные задачи, в чем я убедился, проведя некоторые вычислительные операции, применяя пакет MATLAB. Он удобен в использовании, когда требуется найти значение из больших и сложных формул. |


