ТЕОРИЯ АВТОМОБИЛЕЙ И ДВИГАТЕЛЕЙ Борис. Протокол от 20 г. 20 ж. хаттама міндетті й баылау жмысы

• Название: Протокол от 20 г. 20 ж. хаттама міндетті й баылау жмысы
• Дата: 16.05.2022
• Размер: 0.98 Mb.
• Имя файла: ТЕОРИЯ АВТОМОБИЛЕЙ И ДВИГАТЕЛЕЙ Борис.docx
• Тип: Протокол; #531489
• страница: 1 из 3

ШЫҒЫС ТЕХНИКАЛЫҚ ГУМАНИТАРЛЫҚ КОЛЛЕДЖІ

ВОСТОЧНЫЙ ТЕХНИЧЕСКО-ГУМАНИТАРНЫЙ КОЛЛЕДЖ

БЕКІТЕМІН УТВЕРЖДАЮ

Директордың ОІ Зам. директора по УР

жөніндегі орынбасары _____________

________________ Рассмотрено на заседании ЦМК

ЦӘК отырысында қаралған Протокол №___от «___»______20___г.

«___»______20___ж. №___хаттама __________

___________
МІНДЕТТІ ҮЙ БАҚЫЛАУ ЖҰМЫСЫ

КОНТРОЛЬНАЯ РАБОТА

Оқытушы

Преподаватель Яковлев Владимир Сергеевич

Предмет Теория автомобилей и двигателей

Мамандығы 1201000 «Техническое обслуживание ремонт и эксплуатация

автомобильного транспорта»

Специальность ___________________________________________________________

(шифр и наименование специальности) (мамандықтың шифры мен атауы)

Перечень теоретических вопросов 1-го блока

2. Принцип эквивалентности тепловой и механической энергии. Первый закон термодинамики.
Принцип эквивалентности теплоты и работы является частным случаем первого закона термодинамики — закона сохранения и превращения энергии.

Еще М.В. Ломоносов считал, что «живая сила механического движения превращается в живую силу частиц нагретого тела». В 1798 г. Бенджамин Румфорд, изучая выделение теплоты при сверлении стволов пушек, приходит к выводу, что теплота не является веществом.

Позднее, в 1842 г., Роберт Майер устанавливает связь между теплотой и механической работой, определив механический эквивалент теплоты I = 423,8 кг м/ккал.

В 1843 г. Джеймс Джоуль, проведя уникальный эксперимент, находит, что I = 427 кг м/ккал. Последние исследования показывают, что I = 426,939 кг-м/ккал. На рис. 1 приведена принципиальная схема установки Джоуля.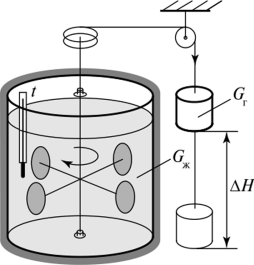



Рис. 1. Схема установки Джоуля
При движении груза массой G_r в поле гравитационных сил совершается механическая работа L над адиабатической системой массой <7_Ж, представляющей собой теплоизолированный сосуд с водой (жидкостью). Балансовое уравнение в этом случае имеет вид



где с_ж — средняя удельная массовая теплоемкость жидкости.

В процессе опытов было обнаружено, что при совершении над системой механической работы, равной 427 кг м, температура воды массой в 1 кг увеличивалась с 14,5 до 15,5 °С, что соответствовало подводу к ТС одной килокалории теплоты.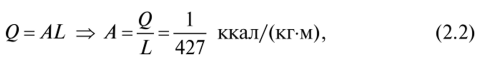



где Л — тепловой эквивалент работы.

Таким образом, Джоулем было доказано, что определенной затраченной механической работе всегда соответствует выделение определенного количества теплоты.

При этом можно говорить уже не об эквивалентности, а о равнозначности всех видов энергии, устанавливаемой законом сохранения и превращения энергии, а следовательно — и Первым законом термодинамики.

Первый закон термодинамики: энергия изолированной системы (Е) при всех ее превращениях остается постоянной и взаимное превращение теплоты (О) и работы (/.) происходит в строго определенных соотношениях, т. е. теплота и работа эквивалентны;

или невозможно создать машину, производящую работу, без того, чтобы не исчезло эквивалентное количество энергии другого вида.

Этот закон отрицает возможность создания вечного двигателя I рода, т. е. нельзя построить двигатель, вырабатывающий энергию (совершающий работу') и при этом не потребляющем другой вид энергии.

Таким образом, согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами:



Гидродинамика._Истечение_жидкости_из_малых_отверстий_и_насадок.__Гидродинамика'>50. Гидродинамика. Истечение жидкости из малых отверстий и насадок.
Гидродинамика – это раздел физики, изучающий свойства жидкостей с помощью законов механики.

Жидкости можно условно разделить на идеальные и неидеальные (реальные).

Идеальные жидкости не «растягиваются» и не «сжимаются» под воздействием внешних сил, они абсолютно подвижны и их молекулы не взаимодействуют друг с другом. Это упрощенная модель, и в жизни подобных жидкостей не существует.

Реальные жидкости – все остальные жидкости. Они бывают в свою очередь ньютоновскими и неньютоновскими.

Гидродинамика относится к физике сплошной среды, она исследует законы движения и равновесия жидкости и газа.

Описывает взаимодействие жидкости (реального газа) с движущимися и неподвижными поверхностями.

Перемещение жидкости принципиально отличается от движения твердых тел. В своем движении жидкость не может сохранять неизменным расстояние между ее частицами. Если рассматривать движение элементарного объема жидкости, то его можно представить как сумму трех движений: поступательного и вращательного перемещения всего объема жидкости как целого, и движение разных частиц рассматриваемого объема по отношению друг к другу. При движении жидкости следует учитывать массовые силы и силы трения (вязкость).

Гидродинамика - раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

Истечение жидкости из малых отверстий

Отверстия подразделяют в зависимости от их размеров на малые и большие. Малыми считаются отверстия, размеры которых малы по сравнению с величиной   напора над центром этого отверстия (рис. 2). Если же размеры отверстия сравнимы с величиной этого напора, то такие отверстия считаются большими. Таким образом, понятие о малости отверстия относительно: одно и то же отверстие при определенных условиях может считаться малым, в то время как в других условиях - большим.

Если отверстие малое, то можно с достаточной степенью точности пренебрегать различием напоров в разных точках этого отверстия. В то же время для больших отверстий нужно учитывать, что напор в разных точках этого отверстия может быть различным.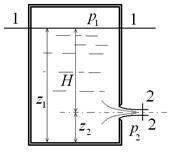

 


Рис. 2. Истечение жидкости из резервуара через малое отверстие

 

Среди множества типов отверстий выделяют отверстия в тонких стенках. Такими называются отверстия, края которых имеют острую кромку, тогда толщина стенки не влияет на форму струи и условия истечения жидкости. Опытом установлено, что стенку можно считать тонкой, если ее толщина   не превосходит 0,2 диаметра отверстия   , т.е.   .

При истечении жидкости через круглое отверстие в тонкой стенке наблюдается явление, схематично изображенное на рис. 3. Линии тока жидкости, начинающиеся на свободной поверхности, сближаются при подходе к отверстию, и это сближение продолжает сохраняться на расстоянии ещё нескольких диаметров за ним. Поскольку частицы жидкости подходят к отверстию по плавно меняющимся траекториям, и отсутствуют силы, способные вызвать скачкообразное изменение скорости, то площадь поперечного сечения струи, вытекающей из круглого отверстия в тонкой стенке, меньше, чем площадь самого отверстия. Это явление называют сжатием струи при истечении из отверстия.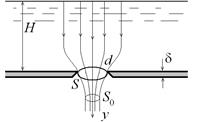

 


Рис. 3. Сжатие струи при истечении через отверстие
Площадь   поперечного сечения струи на некотором расстоянии от отверстия стабилизируется, линии тока в струе становятся параллельными друг другу, а скорости жидкости вдоль них практически равны друг другу. Отношение   площади   в цилиндрической части струи к площади отверстия   называют коэффициентом сжати яструи.

Коэффициент сжатия струи зависит только от формы отверстия; опытами установлено, что при больших числах Рейнольдса для круглого отверстия в тонкой плоской стенке коэффициент сжатия струи составляет величину   .

Вообще же можно показать, что для большинства отверстий величина этого коэффициента изменяется в пределах   .

Если отверстие в стенке не является круглым, то сближение линий тока может приводить к сложным изменениям формы вытекающей струи. Так, например, для прямоугольного отверстия сгущение линий тока в его углах приведет к тому, что струя приобретает форму креста, который за счет сил поверхностного натяжения может периодически изменять свой вид.

Истечение жидкости из насадок

Насадком называется короткая труба, присоединенная к отверстию в тонкой стенке. Насадки имеют различные формы живого сечения и постоянные или меняющиеся размеры основного канала по длине.

 На рис. 4 показаны наиболее распространенные типы насадков: а - наружный цилиндрический насадок (насадок Вентури); б - внутренний цилиндрический (насадок Борда); в - конический сходящийся насадок; г - конический расходящийся насадок; д — коноидальный насадок, выполненный в форме вытекающей струи.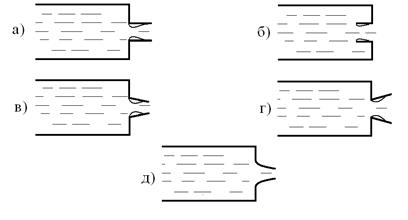

Рис. 4. Истечение жидкости через насадки различной формы

 

Насадки играют большую роль в современной технике. Их применяют для увеличения расхода жидкости через отверстие, измерения расхода жидкости, организации направленного слива, создания струй, имеющих самое различное назначение и применение. Так, например, струями высокого давления разрушаются твердые горные породы и режутся металлы.

Струя жидкости, поступающая в насадок, в большинстве случаев отрывается от стенки насадка у входа благодаря силам инерции частиц жидкости, движущихся по криволинейным траекториям (рис. 5); затем струя расширяется и на выходе заполняет весь насадок. В области отрыва струи от стенок насадка создается пониженное давление, которое как бы дополнительно подсасывает жидкость и тем самым увеличивает ее расход.

Рассмотрим сначала истечение жидкости через внешний цилиндрический насадок (рис. 5).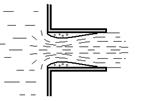

 


Рис. 5. Отрыв струи при входе в насадок

 

Струя жидкости при входе в насадок сжимается, затем постепенно расширяется и заполняет все сечение насадка. Так как выходное сечение насадка полностью заполнено жидкостью, то коэффициент сжатия струи равен 1, а коэффициент расхода

 

 ,   .

 

Таким образом, для этого насадка коэффициент расхода равен коэффициенту скорости.

Составим уравнение Бернулли для жидкости, находящейся между сечениями 1 - 1 и 2 - 2 (рис. 6):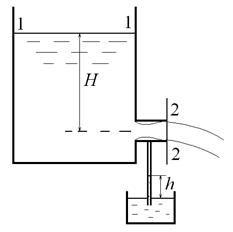

 



 



Рис. 6. Расчет истечения жидкости из резервуара через отверстие с внешним цилиндрическим насадком

 

Так же, как при истечении из отверстия, будем считать, что   Из уравнения Бернулли получим:

 

 (1)

 

Потери напора   складываются из местных потерь напора при входе жидкости в насадок и потерь на расширение струи внутри насадка, т. е.

 



 

Подставив это выражение в формулу (1), найдем скорость 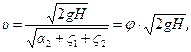  истечения жидкости из насадка:

 



 

где

 .

 

Для расхода   жидкости получим соотношение

 



 

Здесь коэффициент скорости   равен коэффициенту расхода   .

Отметим, что при истечении жидкости через насадки, так же как и при истечении через отверстия, все коэффициенты истечения в общем случае зависят от числа Рейнольдса. Однако при больших числах Рейнольдса коэффициент расхода   перестает зависеть от числа Рейнольдса и становится практически постоянной величиной, равной   .

73. Кинематика КШМ Определение скорости поршня в зависимости от угла поворота коленчатого вала. Пояснение дать с приведением схемы КШМ и графиков изменения скоростей поршня: первого порядка, второго порядка и суммарной скорости от угла поворота коленчатого вала.
Основным звеном энергетической установки предназначенной для транспортной техники является кривошипно-шатунный механизм. Его основной задачей является превращение прямолинейного движения поршня во вращательное движение выходного вала. Условия работы элементов кривошипно-шатунного механизма характеризуются широким диапазоном и высокой частотой повторения знакопеременных нагрузок в зависимости от положения поршня, характера происходящих процессов в объеме цилиндра и частоты вращения коленчатого вала двигателя.

Типовые схемы кривошипно-шатунного механизма, с учетом смещения осей коленчатого вала и оси цилиндров представлены на рисунке 7.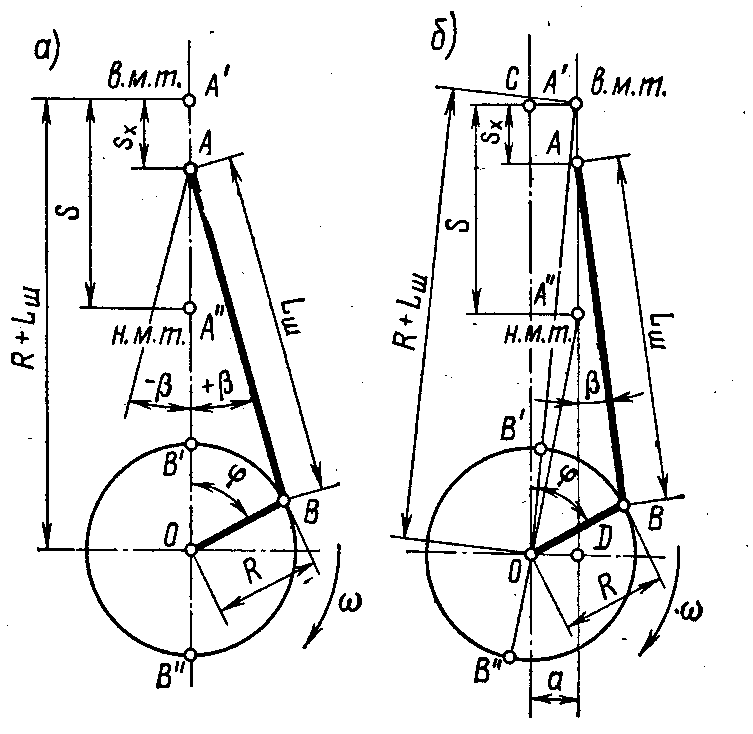


Рис.7. Типовые схемы кривошипно-шатунного механизма

Расчет кинематики и определение динамических сил, возникающих в кривошипно-шатунном механизме, выполняется для заданного номинального режима, с учетом полученных результатов теплового расчета и ранее принятых конструктивных параметров предложенного прототипа.

Основной задачей кинематического расчета является определение перемещения, скорости и ускорения элементов кривошипно-шатунного механизма.

Зависимость перемещения поршня от угла поворота коленчатого вала определяется по формуле: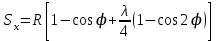


Значения выражения в скобках (для удобства обозначено γ) при углах поворота кривошипа от 00 до 3600 с шагом 30 0 и при λ = 0,25 для простоты расчетов посчитаны и сведены в таблицу. Углы поворота сведены в таблицу 1. График перемещения поршня изображен на рисунке 8.

Таблица 1 - Зависимость перемещения поршня от угла поворота

φ0	γ	r	S
0	0,00	0,055	0,00
30	0,1653	0,055	0,01
60	0,5938	0,055	0,03
90	1,1250	0,055	0,06
120	1,5938	0,055	0,09
150	1,8973	0,055	0,10
180	2,0000	0,055	0,11
210	1,8973	0,055	0,10
240	1,5938	0,055	0,09
270	1,1250	0,055	0,06
300	0,5938	0,055	0,03
330	0,1653	0,055	0,01
360	0,00	0,055	0,00

Перемещение поршня при угле поворота коленчатого вала на 300:

S = 0,1653 0,055 = 0,01 м.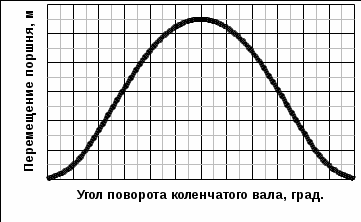

Рис.8. Зависимость перемещения поршня от угла поворота коленчатого вала

Перемещение (путь) поршня будет зависеть от угла поворота коленчатого вала и определяться отрезком Х (см. рис. 9), который равен: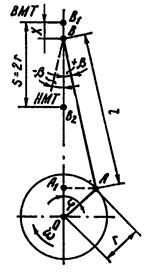

.



Рис. 9. Схема центрального КШМ
Из треугольников А₁ АВ и ОА₁А следует, что



Учитывая, что 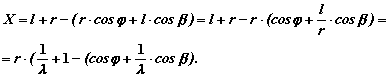 , получаем:



Из прямоугольных треугольников А₁АВ и А₁ОА устанавливаем, что



Откуда


то, подставив полученные выражения в формулу для перемещения поршня, получим: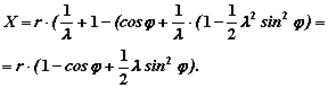



Так как  то



Полученное уравнение характеризует движение деталей КШМ в зависимости от угла поворота коленчатого вала и показывает, что путь поршня можно условно представить состоящим из двух гармонических перемещений:



где  – путь поршня первого порядка, который имел бы место при наличии шатуна бесконечной длины;

– путь поршня второго порядка, т. е. дополнительное перемещение, зависящее от конечной длины шатуна.

На рис. 10 даны кривые пути поршня по углу поворота коленчатого вала. Из рисунка видно, что при повороте коленчатого вала на угол, равный 90°, поршень проходит больше половины своего хода.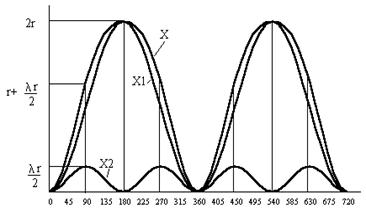



Рис. 10. Изменение пути поршня в зависимости от угла поворота коленчатого вала
Скорость поршня определяется как первая производная пути поршня по времени:



где  –угловая скорость вращения вала.

Скорость поршня можно представить в виде суммы двух слагаемых:



где  – гармонически изменяющаяся скорость поршня первого порядка, т. е. скорость, с которой двигался бы поршень при наличии шатуна бесконечно большой длины;

– гармонически изменяющаяся скорость поршня второго порядка, т. е. скорость дополнительного перемещения, возникающая вследствие наличия шатуна конечной длины.