04.Моделир дискр-стох сист с исп таблицы модели. Протокол 2 от 26. 09. 03 Рекомендованы к печати учебнометодической комиссией специальности 071900
 Скачать 1.89 Mb. Скачать 1.89 Mb.
|
|
Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Кузбасский государственный технический университет» Кафедра информационных и автоматизированных производственных систем моделирование дискретно-стохастических систем с использованием таблицы модели Методические указания к лабораторной работе по дисциплине «Моделирование систем» для студентов специальности 071900«Информационные системы и технологии»Составитель В.В. Зиновьев Утверждены на заседании кафедры Протокол № 2 от 26.09.03 Рекомендованы к печати учебно-методической комиссией специальности 071900 Протокол № 103 от 26.09.03 Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ Кемерово 2003 1. Цель работы Цель работы – изучить метод моделирования дискретно-стохастических систем на основе математического аппарата систем массового обслуживания и таблицы модели. В ходе выполнения лабораторной работы студент должен научиться отображать вычислительную сеть в виде системы массового обслуживания, генерировать входные величины модели по заданному закону распределения и формировать таблицу модели по типу табл. 1.1 при помощи программы табличных вычислений Microsoft Excel (предполагается, что студент знаком с основами работы c Microsoft Excel`97 или Microsoft Excel`2000). Таблица 1.1 Таблица модели
В табл. 1.1 хij(j= 1, 2, .., р) – входные сигналы, yi – отклик для каждого из повторов i= 1, 2 ,…, n. Таблица модели является систематическим методом для отслеживания состояния системы в течение времени. Суть табличного моделирования – получить таблицу модели, которая разрабатывается для каждой конкретной задачи путём добавления соответствующих для поставленной задачи колонок. 2. Теоретические положения 2.1. Дискретно-стохастические модели Дискретно-стохастические модели рассмотрим на примере использования в качестве типовых математических схем систем массового обслуживания (СМО) (англ. queueing system). В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования информационных, производственных, технических, экономических и многих других систем. Например, заявки на обработку информации сервером с удаленных рабочих мест, потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха и др. При этом характерным для работы таких объектов является случайное появление заявок на обслуживание и завершение обслуживания в случайные моменты времени, то есть стохастический характер процесса их функционирования. Система массового обслуживания (СМО) описывается потоком заявок, механизмом обслуживания, вместимостью системы и дисциплиной обслуживания. Эти атрибуты СМО более подробно описаны в [1, 2]. Пример простой СМО изображен на рис. 2.1. 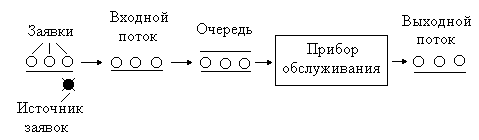 Рис. 2.1. Система массового обслуживания В этой одноканальной однофазной СМО поток заявок бесконечен, то есть если вышедшая заявка становится в очередь на обслуживание, это не влияет на появление следующих заявок, требующих обслуживания. Попадание заявок в прибор обслуживания происходит в случайные моменты времени. Время обслуживания – случайная величина, распределенная в соответствии с каким-либо законом, который с течением времени не меняется. Вместимость системы не ограничена – это значит, что в очереди может находиться сколь угодно много заявок. Заявки обслуживаются по принципу первый пришел – первый обслужен. Приход заявок и обслуживание осуществляются по некоторым законам распределения. Прежде чем перейти к примеру моделирования, необходимо ввести такие определения, как состояние системы, событие и модельное время. Эти концепции более подробно изложены в [1, 2, 3]. Состояние системы – это количество заявок в системе и состояние прибора обслуживания (занят или не занят). Событие – это набор обстоятельств, вызывающих мгновенное изменение состояния системы. Приведенная на рис. 2.1 СМО включает в себя прибор обслуживания, обслуживаемую заявку (если прибор обслуживания занят) и заявки, ожидающие в очереди (если таковые имеются). Когда заявка освобождает прибор обслуживания, далее процесс идёт, как показано на рис. 2.2. 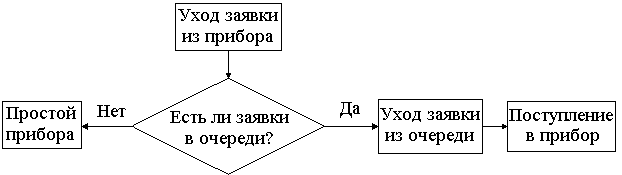 Рис. 2.2. Алгоритм действий после освобождения прибора обслуживания Событие поступления возникает, когда заявка входит в систему. Схема потока поступления показана на рис. 2.3. 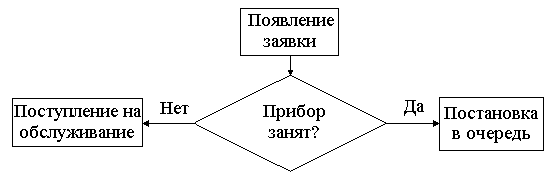 Рис. 2.3. Движение заявки после поступления в СМО В момент поступления заявки прибор обслуживания может быть свободен либо занят и, соответственно, либо сразу приступит к обслуживанию, либо заявка попадает в очередь. После завершения обслуживания прибор либо освобождается, либо переходит к обслуживанию следующей заявки. Если очередь есть, следующая по очереди заявка попадает в прибор обслуживания и занимает его. Если же очереди нет, после завершения обслуживания прибор обслуживания будет свободен. После завершения обслуживания и в случае отсутствия очереди прибор не может быть занят. Точно так же он не может быть свободным после завершения обслуживания, если в очереди заявки ещё есть. При моделировании реальных систем при помощи СМО, как правило, определяются следующие параметры: 1. Среднее время ожидания заявки в очереди перед прибором: где Tож – общее время ожидания всех заявок в очереди; nож – количество заявок, которые ожидали в очереди. 2. Вероятность ожидания заявки в очереди: где N – общее количество заявок. 3. Вероятность простоя прибора обслуживания: где Tпр – общее время простоя прибора; T – общее модельное время. 4. Среднее время обслуживания заявки прибором, которое теоретически находится по формуле гдеtо1, to2, ..., ton– возможные значения случайной величины времени обслуживания заявки прибором; p1, p2, ..., pn – соответствующие им вероятности. Упрощенно это значение можно найти по формуле где Tо – общее время обслуживания заявок прибором. 5. Среднее значение интервала времени между появлениями заявок где aиb – соответственно начало и конец интервала, на котором распределена случайная величина. Упрощенно среднее значение интервала времени между появлениями заявок можно определить по формуле где I – общее время между появлениями заявок (единица вычитается из знаменателя, потому что время появления первой заявки принимается равным 0). В п. 4 и п. 5 теоретические значения среднего времени обслуживания и среднее значение интервала времени между появлениями заявок могут отличаться от значений, рассчитанных по упрощенным формулам. При увеличении времени моделирования (при увеличении количества обслуженных заявок) это расхождение будет уменьшаться. 6. Среднее время нахождения заявки в системе можно определить двумя способами. Первый способ – по формуле где Tз – общее время нахождения заявок в системе. Второй способ – по формуле где Для получения статистической значимости результатов моделирования необходимо проводить множество реализаций, меняя последовательности псевдослучайных чисел, а затем по выборке определять требуемые параметры. Точность результатов будет увеличиваться при увеличении количества реализаций [4]. Также при моделировании необходимо учитывать начальные условия [1, 3]. Но цель выполняемой лабораторной работы – изучить методологию моделирования простых дискретно-стохастических систем при помощи таблицы модели, а не в том, чтобы давать достоверную оценку результатов и выносить рекомендации, какие изменения нужно проводить в системе. 2.2. Моделирование случайных событий При моделировании события обычно возникают во времени с определенной вероятностью, эта вероятность имитирует случайность событий в реальной системе. Например, нельзя сказать с уверенностью, когда появится сбой при передаче данных по каналу связи или когда произойдет переполнение буферных регистров, хранящих пакеты данных. В этих случаях статистическая модель будет формироваться из данных, собранных и подвергнутых анализу, либо субъективных вероятностей и уравнений. Случайность событий моделируется с помощью «вероятностей» [4]. Случайные числа могут быть сгенерированы, например, при помощи программы табличных вычислений типа Microsoft Excel. Для моделирования дискретно-стохастической системы необходимо поставить искусственный эксперимент, отражающий основные условия ситуации. Для этого необходимо использовать способ имитации искусственной последовательности появления заявок и времени их обслуживания прибором. Один из способов, который можно применить, состоит в использовании встроенного в программу табличных вычислений Microsoft Excel Пакета анализа, который позволяет генерировать случайные числа с различными распределениями. Такие множества случайных чисел используются в методе Монте-Карло и других методах моделирования. Через меню Microsoft Excel напрямую доступны 6 типов распределений: Равномерное (Uniform), Нормальное (Normal), Бернулли (Bernouli), Биномиальное (Binomial), Пуассона (Poisson) и Дискретное (Discrete) (определяемое пользователем). Запустите Microsoft Excel. В меню «Сервис» выберите команду «Анализ данных», затем в списке «Инструменты анализа (Analysis Tools)» окна диалога «Анализ данных» укажите пункт «Генерация случайных чисел» и нажмите кнопку «ОК». Microsoft Excel откроет окно диалога, подобное показанному на рис. 2.4. 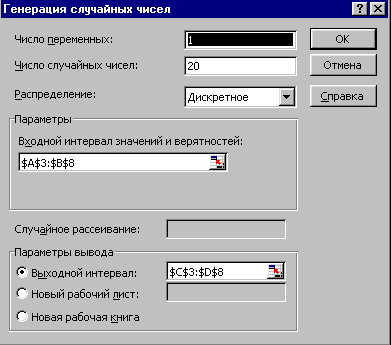 Рис. 2.4. Окно диалога «Генерация случайных чисел» при задании дискретного распределения В полях «Число переменных (Number Of Variables)» и «Число случайных чисел (Number Of Random Numbers)» укажите нужное количество столбцов и случайных чисел, которое вы хотите получить в каждом столбце. Например, если нужно создать 2 столбца по 20 чисел в каждом, задайте 2 в поле «Число переменных» и 20 в поле «Число случайных чисел». Область «Параметры (Parameters)» окна диалога «Генерация случайных чисел (Random Number Generation)» изменяется в зависимости от выбранного типа распределения. В поле «Случайное рассеивание (Random Seed)» вы можете также задать производящее значение, которое определяет получаемую последовательность случайных (псевдослучайных) чисел. В этом случае при каждой генерации случайных чисел определенного типа распределения и при использовании одного и того же производящего значения вы будете получать каждый раз одинаковую последовательность чисел. Учитывая это, производящее значение следует задавать в том случае, если вам необходимо несколько раз воспроизвести одну и ту же последовательность случайных чисел. Для всех типов распределения в поле «Выходной интервал (Output Range)» задается диапазон размещения случайных чисел. Если указанный диапазон уже содержит данные, то прежде чем на место этих данных будут записаны случайные числа, на экране появится предупреждение. 3. задание к работе Локальная вычислительная сеть (ЛВС) состоит из сервера и 3-х рабочих станций. Интервалы поступления заявок (ti) на сервер и их вероятности (pi) представлены в табл. 3.1. Время обработки заявок (T), поступающих от станций, распределено нормально с математическим ожиданием () и стандартным отклонением (), приведенными в табл. 3.2. Таблица 3.1 Распределение интервалов поступления заявок в секундах (по вариантам)
Таблица 3.2 Распределение времени обработки заявок в секундах (по вариантам)
При выполнении задания данной лабораторной работы необходимо отобразить функционирование ЛВС в виде СМО, а затем сформировать таблицу модели при помощи программы табличных вычислений Microsoft Excel, которая позволит определить при обработке сервером 20 заявок следующие характеристики: - среднее время ожидания заявки в очереди перед сервером; - вероятность ожидания заявки перед сервером; - вероятность простоя сервера; - среднее время обслуживания заявки сервером; - среднее значение интервала времени между появлениями заявок; - среднее время нахождения заявки в ЛВС. 4. Порядок выполнения работы 1. Ознакомьтесь с методическими указаниями по выполнению данной лабораторной работы. 2. Получите у преподавателя вариант задания. 3. Представьте работу локальной вычислительной сети в виде системы массового обслуживания. 4. Составьте по заданному варианту таблицу модели, используя программу табличных вычислений Microsoft Excel. 5. Проведите эксперимент с моделью локальной вычислительной сети для получения требуемых характеристик при обработке 20 заявок. Время на выполнение данной лабораторной работы – 2 часа. 5. Пример выполнения работы Процедуру табличного моделирования покажем на примере функционирования некоторой вычислительной системы (ВС). Пусть в ВС к ЭВМ подключено несколько терминалов, с которых осуществляется выполнение заданий определенного класса. Причем, если хоть с одного терминала выполняется задание, остальные терминалы вынуждены простаивать из-за нехватки производительности ЭВМ. Интервалы появления заданий равновероятны и приведены в табл. 5.1 (для простоты время округлено до ближайшего целого числа – секунд). Время выполнения любого задания ЭВМ колеблется от 1 до 6 секунд с вероятностью, представленной в табл. 5.2. Таблица 5.1 Распределение времени между появлениями заданий
Таблица 5.2 Распределение времени выполнения заданий
А) Представим вычислительную систему в виде системы массового обслуживания. Работу данной ВС можно отобразить одноканальной (заявка может обслуживаться параллельно только одним прибором), однофазной (после обслуживания одним прибором заявка не поступает на следующий), разомкнутой (заявка после обслуживания покидает систему), без потерь (заявке разрешается ждать в очереди) системой массового обслуживания (рис. 5.1). 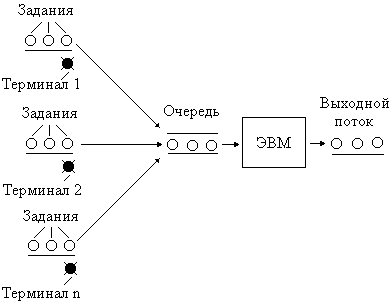 Рис. 5.1. Модель вычислительной системы в виде СМО В СМО заявками являются задания, которые с заданной вероятностью поступают на обслуживание в прибор – ЭВМ. Входной поток представляет собой неограниченное количество заданий. Вначале источники (терминалы) генерируют заявки, поставляя их во входной поток. Из-за разницы скорости обслуживания прибора и скорости поступления заявок перед прибором образуется очередь. После обслуживания (с заданной вероятностью) заявки покидают систему. Б) Проанализируем СМО, создав табличную модель появления и обслуживания 20 заявок. Для моделирования данной системы необходимо использовать способ имитации искусственной последовательности появлений заявок и времени, необходимого для обслуживания каждой заявки. Таким образом, можно получить временные ряды, представляющие промежутки времени между последовательными появлениями заданий и соответствующие им времена обслуживания. Используя встроенный в Microsoft Excel Пакет анализа, получим 20 (согласно заданию) равномерно распределённых случайных чисел, которые определяют интервалы появления заданий. Выбрав в меню «Сервис» команду «Анализ данных», в списке «Инструменты анализа» укажем пункт «Генерация случайных чисел» и нажмем «ОК». В окне диалога в поле «Число переменных» поставим 1, а в поле «Число случайных чисел» укажем 19 (интервал появления первой заявки равен 0). В поле «Распределение» выберем «Равномерное». В области «Параметры» укажем диапазон чисел от 1 до 9 (9 не включая), в интервале которых должны генерироваться числа. В поле «Выходной интервал» зададим диапазон размещения случайных чисел, например А1:А19 (рис. 5.2). 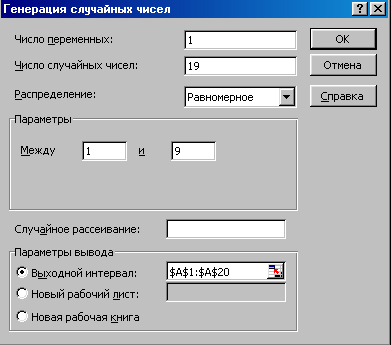 Рис. 5.2. Окно диалога для задания равномерно распределенных интервалов поступления заявок После нажатия кнопки «ОК» окна диалога в ячейках А1:А19 появятся сгенерированные числа. Распределение интервалов между появлениями заявок показано в табл. 5.3 (значения округлены до секунд). Таблица 5.3 Интервалы времени между появлениями заявок
Для генерирования времени обслуживания заявок воспользуемся инструментом «Дискретное распределение». Зададим в соответствии с табл. 5.2 возможные значения случайной величины и их вероятности в виде двух столбцов рис. 5.3. 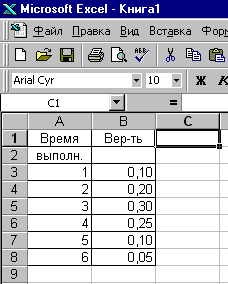 Рис. 5.3. Задание в Microsoft Excel значений времени обслуживания заявок и их вероятностей Используя окно диалога «Генерация случайных чисел», зададим дискретное распределение (см. рис. 2.4). Сгенерированное время обслуживания 20 заявок представлено в табл. 5.4. Таблица 5.4 Сгенерированное время обслуживания заявок
Используя сгенерированные значения интервалов поступления заявок и их обслуживания, сформируем таблицу модели (табл. 5.5). Таблица 5.5 Таблица модели
Первая заявка (первое задание на ЭВМ с терминалов) пришла в момент времени 0 c. Ее обслуживание (выполнение задания) началось немедленно и закончилось в момент времени 4 c. Таким образом, заявка (задание) находилась в системе 4 с. Вторая заявка появилась в момент времени 8 с, сразу попала в прибор и обслуживалась в течение 1 с. Таким образом, прибор обслуживания простаивал 8–4=4 с. Четвертая заявка появилась в момент времени 15 с, но не обслуживалась до момента модельного времени – 18 с, что соответствует окончанию обслуживания предыдущей заявки. Четвертая заявка находилась в ожидании (в очереди) 18–15=3 с. И так далее. Дополнительные столбцы таблицы модели предназначены для отображения статистической информации относительно времени нахождения заявок в системе, времени простоя прибора обслуживания после ухода предыдущей заявки (если такой факт имеет место). В конце таблицы произведен подсчет итоговой статистики для времени обслуживания, времени ожидания в очереди, времени нахождения заявок в системе и времени простоя прибора обслуживания. Следует отметить, что записи в табл. 5.5 упорядочены по времени, в этом случае события могут быть упорядочены по номеру заявки (задания), а могут быть и не упорядочены. Расположение событий в хронологическом порядке является основой дискретного моделирования. Рис. 5.4 дает информацию о количестве заявок в системе в различные моменты времени. 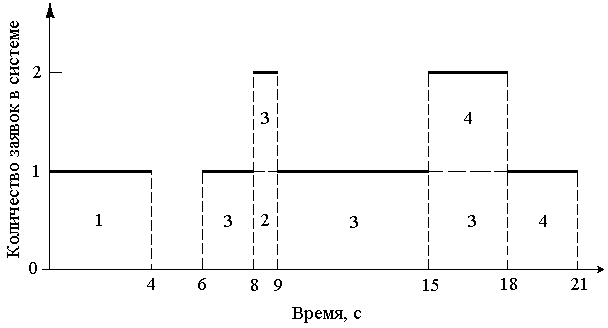 Рис. 5.4. Количество заявок в системе Это визуальное изображение содержимого табл. 5.5. Заявка № 1 находится в системе от 0 до 4 с. С 4 до 6 с заявок в системе нет. Заявка № 2 прибывает в 8 с и уходит в 9 с. В некоторые периоды времени в системе бывает по две заявки, например, с 8 до 9 с в системе находятся заявки № 2 и № 3, а с 15 до 18 с – № 3 и № 4. Бывают моменты времени, в которые события происходят одновременно, как, например, в 53 с, когда уходит заявка № 10 и прибывает заявка № 13 (на рис. 5.4 не показано, см. табл. 5.5). В) Используя табл. 5.5, определим следующие характеристики системы, полученные при моделировании: 1. Среднее время ожидания заявки в очереди перед прибором:
2. Вероятность ожидания заявки в очереди: 3. Вероятность простоя прибора обслуживания: 4. Среднее время обслуживания заявки прибором:
5. Среднее значение интервала времени между появлениями заявок:
6. Среднее время нахождения заявки в системе:
Вывод Большинство заявок стоит в очереди (65 %), однако среднее время ожидания не превышает допустимого значения и составляет 4,3 с. Время простоя прибора обслуживания не превышает 25 % от времени моделирования. 6. Требования к отчету Отчет о работе должен содержать: 1. Задание и исходные данные по заданному варианту лабораторной работы. 2. Модель ЛВС в виде СМО и таблицу модели, построенную в Microsoft Excel. 3. Результаты моделирования, анализ полученных результатов и выводы по работе. 7. Контрольные вопросы 1. Что такое таблица модели? 2. Приведите элементы СМО, используемые для представления функционирования вычислительных систем. 3. Какие события происходят после освобождения прибора обслуживания и поступления заявки в СМО? 4. Для чего применяют инструмент «Генерация случайный чисел» встроенного в программу табличных вычислений Microsoft Excel Пакета анализа? 5. Какие виды распределений случайных величин можно задавать в Microsoft Excel? 6. Как задать равномерное, нормальное и дискретное распределения в Microsoft Excel? 8. Список рекомендуемой литературы 1. Советов Б.Я. Моделирование систем: Учеб. для вузов. – 3-е изд., перераб. и доп. / Б.Я. Советов, С.А. Яковлев. – М.: Высш. шк., 2001. 2. Кузин Л.Т. Основы кибернетики: В 2 т. Т. 2. Основы кибернетических моделей: Учеб. пособие для вузов. – М.: Энергия, 1979. 3. Шеннон Р. Имитационное моделирование систем – искусство и наука. – М.: Мир, 1978. 4. Макарова Н.В. Статистика в Excel: Учеб. пособие / Н.В. Макарова, В.Я. Трофимец. – М.: Финансы и статистика, 2002. Оглавление
Составитель Василий Валентинович Зиновьев моделирование дискретно-стохастических систем с использованием таблицы модели Методические указания к лабораторной работе по дисциплине «Моделирование систем» для студентов специальности 071900«Информационные системы и технологии»Редактор А.В. Дюмина Подписано в печать 13.10.03. Формат 60х84/16. Бумага офсетная. Отпечатано на ризографе. Уч.-изд. л. 1,2. Тираж 75 экз. Заказ ГУ КузГТУ. 650026, Кемерово, ул. Весенняя, 28. Типография ГУ КузГТУ. 650099, Кемерово, ул. Д. Бедного, 4 А. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
