Информатика и ИКТ лекция. Протокол умс от 201 г. Проректор по умр с. П. Ермишин
 Скачать 5.78 Mb.
|
2.3. Лабораторный практикум по дисциплинеРаспределение тем лабораторных занятий по времени
Содержание лабораторных занятий ЛАБОРАТОРНАЯ РАБОТА №1. « КОДИРОВАНИЕ ИНФОРМАЦИИ» Цель: изучить меры измерения количества информации и кодирование информации. Задачи:
Краткая теория по теме: Кодирование информации. В процессе преобразования информации из одной формы представления (знаковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем. В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре выполняется его кодирование, т. е. преобразование в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс — декодирование, когда из компьютерного кода знак преобразуется в графическое изображение. Кодирование изображений и звука. Информация, в том числе графическая и звуковая, может быть представлена в аналоговой или дискретной форме. При аналоговом представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно. Примером аналогового представления графической информации может служить, скажем, живописное полотно, цвет которого изменяется непрерывно, а дискретного — изображение, напечатанное с помощью струйного принтера и состоящее из отдельных точек разного цвета. Графическая и звуковая информация из аналоговой формы в дискретную преобразуется путем дискретизации, т. е. разбиения непрерывного графического изображения и непрерывного (аналогового) звукового сигнала на отдельные элементы. В процессе дискретизации производится кодирование, т. е. присвоение каждому элементу конкретного значения в форме кода. Дискретизация — это преобразование непрерывных изображений и звука в набор дискретных значений, каждому из которых присваивается значение его кода. Кодирование символьной информации Один байт может иметь 28 = 256 числовых кодов. Этого достаточно, чтобы ими закодировать заглавные и строчные символы латинского алфавита и кириллицы, знаки и специальные символы. Существует несколько стандартов кодирования символов, в которых один символ кодируется одним байтом. Наиболее распространенные приведены в таблице 1.1. Таблица 1.1. Кодирования ASCII (32.. 127) и Windows 1251(128..255) 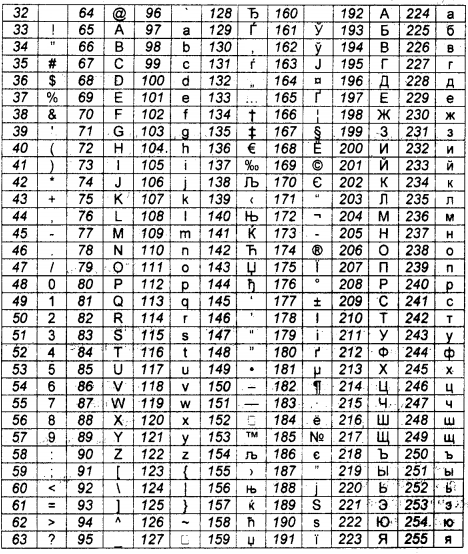 В системе кодировок коды с 0 по 31 отведены под управляющие символы, они невидимы на экране в текстовом режиме (видимы только при специальных режимах). Например, код 9 (Tab), если он встречается в строке, выводит следующий за ним символ в позицию правой ближней метки, код 8 - сдвигает курсор влево на одну позицию, удаляя из нее символ, код 27 - отменяет происходящую операцию, код 13 - переводит курсор на следующую строку, а в сочетании с кодом 10 устанавливает курсор в начало следующей новой строки. Коды с 48 по 57 отведены под символы цифр. Код любой цифры равен 48 + цифра. В приведенном стандарте символы алфавитов упорядочены по возрастанию, и можно заметить, что латинские заглавные буквы начинаются с кода 65, латинские строчные - с кода 97, русские заглавные буквы начинаются с кода 160, строчные - с кода 192 (разница между кодами одного символа строчного и заглавного регистра равна 32). Над текстом, представляющим собой последовательность символов можно производить различные операции: вычислять длину строки (количество символов, включая управляющие и невидимые, например, пробел), сравнивать их коды (посимвольно с начала строки), анализировать, используя логические операции (И- логическое умножение, ИЛИ - логическое сложение, НЕ - логическое отрицание) . Пусть есть строка символов: Зри в корень!. Анализ строки: Длина строки равна 13 символам. , Коды символов, которые будут записаны в памяти машины, следующие: 199 240 232 32 226 32 234 238 240 229 237 252 33. Если это выражение в тексте представляет собой строку, то к этим числовым кодам символов добавляются управляющие коды перевода и начала строки, т.е. 13 и 10. Сравнение двух слов в строке: Зри и корень: 199 240 232 и 234 238 240 229 237 252. Сравнение идет посимвольно, и можно установить по кодам символов «3», «к»: 199<234, поэтому верно будет утверждение "Зри" < "корень". Приведем еще пример: пусть Х= "Объем", У= "Информация" , тогда (ДЛИНА (X) > ДЛИНА (У)-2) И (Х> У) = Ложь (ДЛИНА(Х)<ДЛИНА(У)) ИЛИ(Х<У) = Истина Задание 1. Записать коды символов, которые хранят строки крылатых слов (без учета кавычек). Между словами считать один пробел: 1) "Потемкинские деревни." 6) "Любви все возрасты покорны." 2) "Посеять зубы дракона." 7) "Камень преткновения." 3) "Что и требовалось доказать." 8) "Небо в алмазах..." 4) "Распалась связь времен." 9) "Патронов не жалеть!" 5) "Народ безмолвствует..." 10) "О времена! О нравы!" Задание 2. Подсчитать объем памяти в байтах, занимаемый строками Пушкинских стихов (без учета кавычек; пустые промежутки заполнены одним пробелом; перевод строки считать двумя символами) : 1) "Благослови, поэт! В тиши парнасской сени Я с трепетом склонил пред музами колени... " 2) "Мой жребий вынул Феб, и лира мой удел. Страшусь, неопытный, бесславного паденья... " 3) "С небес уже скатилась ночи тень, Войта заря, сияётбледный день... " 4) "Я говорил: в отечестве моем Где верный ум, где гений мы найдем? " 5) "Любви, надежды; тихой славы недолго тешил нас обман, Исчезли юные забавы, как сон, как утренний туман; " 6) "Пока свободою горим, пока сердца для чести живы, Мой друг, отчизне посвятим души прекрасные порывы!" 7) "Я здесь от суетных оков освобожденный, Учуся в истине блаженство находить..." 8) "С тех пор не целую прелестных очей, С тех пор я не знаю веселых ночей. " 9) "Я пережил свои желанья, я разлюбил свои мечты; Остались мне одни страданья, плоды сердечной пустоты. " 10) "Вуединении мой своенравный гений Познал и тихий труд, и жажду размышлений. " Задание 3. Получить верное утверждение, заменив знак вопроса операцией отношения (=,>,<,<>). 1) "Темп" ? "темпы" 2) "ключ" ? "Ключи" 3) "АЛГОРИТМ" ? "алгоритм" 4) "форма" ? "телевидение" 5) "56" ? "1127" , 6) "Реальность" ? "Реалии" 7) "квадрат" ? "КВАДРАТ" 8) "345" ? "80" 9) "поколение" ? "Поколоть" 10) "Ц283" ? "Ц6" Задание 4. . Какие слова записаны в ячейки ОЗУ, если они содержат значения : 1) 196 206 202 211204 197 205 210 2) 199 192 207 208 206 209 3) 192 208 195 211204 197 205 210 4) 194 203 206 198 197 205 200 197 5) 199 192 217 200210 192 6) 193 192 203 192 205 209 7) 209 210 206 203 193 197 214 8) 199 192 195 208 211 199 202 192 9) 212 206 208 204 211203 192 10) 200 204 207 206 208 210 Задание 5. Вычислить логические выражения с текстовыми константами: 1) X = "Машина" , У = "Запись" (ДЛИНА(Х)= ДЛИНА(У)+1) И (Х>У) (ДЛИНА(Х)= ДЛИНА(У)+1) ИЛИ (Х>У) 2) X = "Алгоритм" , У = "Программа" (ДЛИНА(Х)< ДЛИНА(У)-1) И (Х<У) (ДЛИНА(Х)< ДЛИНА(У)-1) ИЛИ (Х<У) 3) X = "Способ" , У = "Обработка" (ДЛИНА(Х)= ДЛИНА(У)-2) И (Х>У) (ДЛИНА(Х)= ДЛИНА(У)-2) ИЛИ (Х>У) 4) X = "Наука" , У = "Предел" (ДЛИНА(Х)= ДЛИНА(У-1) И (Х>У) (ДЛИНА(Х)= ДЛИНА(У-1) ИЛИ (Х>У) 5) X = "Интеграл" , У = "Длина" (ДЛИНА(Х)= ДЛИНА(У)+2) И (Х<>У) (ДЛИНА(Х)= ДЛИНА(У)+2) ИЛИ (Х<>У) 6) X = "Фотография" , У = "Хранение" (ДЛИНА(Х)- ДЛИНА(У)=2) И (Х>У) " (ДЛИНА(Х)- ДЛИНА(У)=2) ИЛИ (Х>У) 7) X = "Сервер" , У = "IP-ключ" (ДЛИНА(Х)= ДЛИНА(У)-2) И (Х>У) (ДЛИНА(Х)= ДЛИНА(У)-2) ИЛИ (Х>У) 8) X = "Определение" , У = "Знак" (ДЛИНА(Х)- ДЛИНА(У)+6) И (Х>У) (ДЛИНА(Х)- ДЛИНА(У )+6) ИЛИ (Х>У) 9) X = "Тест" , У = "Опрос" (ДЛИНА(Х)+1 > ДЛИНА(У)) И (Х>У) (ДЛИНА(Х)+1 > ДЛИНА(У)) ИЛИ (Х>У) 10) X = "Команда" , У = "Комментарий" (ДЛИНА(Х)< ДЛИНА(У)-З) И (Х<>У) " (ДЛИНА(Х)< ДЛИНА(У)-З) ИЛИ (ХоУ) Кодирование графических изображений Существуют разные способы кодирования графических изображений (векторное, фрактальное, растровое), но при выводе на экран все виды кодов графических изображений преобразуются в растровый код. Каждая точка (пиксель) получает свой цифровой код цвета. Значение кода зависит от числа бит (этот параметр называют иногда глубиной цвета), выделенного для кодирования палитры цветов. Если цвет точки кодируется одним битом, то рисунок может быть черно-белым (двухцветным) и коды цвета: 0 и 1, если четырьмя битами, то палитра шестнадцатицветная с кодами 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. Количество цветов палитры определяется возможным количеством кодов и равно 2N, где N - число бит, выделенных под код цвета палитры. Пример. Пусть имеется черно - белый рисунок 7х 8 точек. Каждая точка кодируется 1 битом, содержащим цвет: 0 - белый, 1 - черный.
Пример. Пусть рисунок выполнен в серых оттенках и палитра состоит из 4 цветов: 0 - белый, 1 - светло-серый, 10 -темносерый, 11-черный. Для кодирования точки требуется 2 бита, а для 56 точек рисунка требуется 2x56= 112 бит, или 112/8= 14 байт
В 256 цветной палитре необходимо 8 бит для кодирования одного цвета точки. Для рисунка 100x100 точек потребуется объем памяти: 8 бит х 100 х 100=80 000 бит, или 10000 байт, или 10000/ 1024 = 9,8 кб.  Задание 6.Закодировать графическое изображение двухцветной палитрой и записать его в двоичном и шестнадцатиричном кодах.  \ 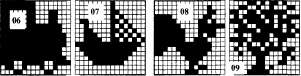 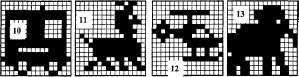 Задание 7. Рисунок имеет размеры а*b точек. Подсчитать объем памяти в байтах занимаемый при растровом кодировании изображения с цветной палитрой:
Задание 8. На мониторах Х" установлено оптимальное разрешение (14":640x480 пиксель, 15": 800х600 пиксель, 17":1024х768 пиксель, 19":1280xl024 пиксель). Изображение занимает 1/k часть экрана. Какой объем видеопамяти в килобайтах будет занимать растровый код изображения с 65536 цветной палитрой?
1. Подсчитать число бит для кодирования одной точки. 2. Подсчитать число точек экрана 3. Подсчитать число точек рисунка. 4. Вычислить объем растрового кода рисунка. Задание 9. Растровый код занимает X Кб. Какую примерную часть экрана при разрешении 1024х768 пикселей будет занимать рисунок при 63536 цветной палитре.
1.Подсчитать число бит для кодирования одной точки. 2. Подсчитать число точек экрана. 3. Подсчитать число точек рисунка. 4. Подсчитать какую часть экрана занимает рисунок. Вопросы для самоконтроля: 1. Что такое кодирование информации в общем смысле? 2. Каково место кодирования среди процессов обработки информации? 3. Какие коды называются двоичными? Приведите примеры. 4. Какой код используется для кодирования букв латинского алфавита буквами персонального компьютера? 5. Какие коды используются в вычислительной технике для кодирования букв русского алфавита? 6. Как кодируется графическая информация, если изображение черно-белое (цветное)? ЛАБОРАТОРНАЯ РАБОТА №2. «ИНФОРМАЦИЯ И ЭНТРОПИЯ» Цель работы: изучить теоретическое понимание энтропии, ее свойства и практическое применение при решении задач. Задачи:
Краткая теория по теме: Рассмотрим количество информации с точки зрения возможности передачи данных сообщений оптимальным образом. Основные положения: 1) количество информации не зависит от способа ее передачи; 2) длина сообщений об одном и том же факте определяется числом качественных признаков вторичного алфавита, но количество информации от длины этого сообщения не зависит; 3) количество информации зависит от числа сообщений, если каждое из них устраняет неизвестность о передаваемом факте. Число сообщений N, которое можно получить, комбинируя m символов алфавита по n элементов в сообщении  (1)Как видим, число сообщений N, а вместе с ним и количество передаваемой информации находятся в экспоненциальной зависимости от количества элементов в сообщении. Поэтому N нельзя непосредственно использовать как меру количества информации. Комбинируя два символа по 3 в сообщении можно передать восемь сообщений, по 4 – шестнадцать, по 5 – тридцать два и т.д. В 1929 г. американский ученый Р. Хартли предложил в качестве меры количества информации принять логарифм числа возможных последовательностей символов:  (2)Основание логарифма зависит от выбранной единицы количества информации. В выражениях, где могут быть использованы двоичные, десятичные и натуральные логарифмы, основание логарифма не ставится. При использовании двоичного логарифма информация измеряется в битах. Пусть для составления сообщения имеется k знаков, обладающих m качественными признаками и pi – вероятность появления каждого качественного признака или символа. Шенноном было получено соотношение для определение среднего количества информации в сообщении с произвольными вероятностями появления значений символов:  (3)При равновероятностных символах, т.е. при pi = 1/m, формула Шеннона переходит в формулу Хартли:   (4)Чем больше априорная неопределенность, тем больше количество информации получается при снятии ее. В этом смысле неопределенность является удобной меры оценки количества информации. В теории информации мерой неопределенности является энтропия – удельное количество информации, приходящееся на один элемент сообщения (на букву первичного алфавита). Для сообщения из k элементов эта величина равна  (5)и называется средней энтропией сообщения. В случае одинаковой вероятности появления любого из m элементов сообщения  (6)Таким образом, если при передаче информации не было информационных потерь, то количество информации на символ сообщения будет точно равно Н, а количество информации при передаче символов  .Следует делать различие между понятиями «количества информации» и «объем информации». Количество информации вычисляется относительно первичного алфавита, а объем информации – относительно вторичного алфавита. Объем информации зависит от длины сообщения во вторичном алфавите n и равен  (7)k – число символов первичного алфавита в сообщении n – число символов вторичного алфавита для кодирования 1 символа первичного алфавита. Энтропия - это мера неопределенности некоторого опыта, исход которого зависит от выбора одного элемента из множества исходных. Множество исходных элементов называется выборочным пространством. Вероятности нахождения элементов исходного множества в том или ином состоянии есть числа положительные, а сумма их равна 1 (в противном случае результат опыта не относился бы к полной группе событий). Выборочное пространство и его вероятностные характеристики представляют собой ансамбль сообщений. Для дискретного ансамбля вероятность события равна сумме вероятностей элементов выборочного пространства, содержащихся в этом событии. Ансамбль сообщений на выходе источника будем называть ансамблем источника сообщений и обозначать буквой А. Абстрактный алфавит, при помощи которого мы представляем исходное множество элементов источника сообщений, обозначается {а1 , а2 , ..., а i,..., ат }. Вероятности появления буквы на выходе источника сообщений обозначим  (8) В этом случае энтропия источника сообщений и представляет собой неопределенность появления на выходе источника сообщений буквы первичного алфавита.  (9)Ансамбль сообщений на входе приемника будем называть ансамблем приемника сообщений и обозначать буквой В. Для того чтобы отличить переданные и принятые сигналы, абстрактный алфавиту в котором представлен ансамбль приемника сообщений, обозначается (b1 , bг, ..., bi, ...,bm,}, а соответствующие вероятности - p(b1); p(b2),... .... р (bi), ..., р (bт). Энтропия приемника сообщений.  (10)и представляет собой неопределенность появления на входе приемника буквы после ее появления на выходе источника сообщений. Если в канале связи не происходит потерь информации, то всегда буква % соответствует букве b1а2 - b2 и т. д. При этом Н (А) = Н (В). Понятие энтропии используется не только при передаче сообщений. Энтропия широко применяется для описания состояния механических и термодинамических систем, для изучения свойств алфавитов различных языков, при исследовании экономических систем и т. д. При исследовании свойств энтропии наибольший интерес представляет ее зависимость от числа m возможных признаков (качеств) и вероятности рi появления в сообщении элемента с i-м признаком. Энтропия характеризует меру неопределенности совокупности событий, составляющих полную группу сумма вероятностей появления отдельных событий должна быть равна единице, т.е.  .Если m = i = 1, т.е. передается сообщение с одним i-м признаком и вероятность его появление pi=1, то  (11) (12)Это очевидно, так как заранее известно, что будет передано сообщение с i-м признаком и при его получении ничего нового мы не узнаем, т. е. получим нулевую информацию. Если сообщение заранее известно, то энтропия минимальна и равна 0. Если вероятность появления i-гo признака в ансамбле сообщений равна нулю, то слагаемое с этим признаком принимает вид неопределенности типа нуль, умноженный на бесконечность. Итак, энтропия есть величина вещественная и имеет экстремум. Так как логарифмы правильных дробей отрицательны, то энтропия опыта с конечным числом исходов всегда положительна. Пример. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Кбайта. Арифметически переведем информационный объем сообщения в биты: I =1,25*1024*8= 10 240 бит. Определить количество бит, приходящееся на один символ: 10 240 бит : 2 048 = 5 бит. По формуле (1) определить количество символов в алфавите: N = 2I = 25 лг= 32. Задача 1. Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1/512 часть одного мегабайта? Задача 2. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере, равна 256. Какое количество информации в байтах может ввести пользователь в компьютер за 1 минуту? Задача 3. Система оптического распознавания символов позволяет преобразовывать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65536 символов. Какое количество информации будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов? Задача 4. Тексты, составленные из 32 букв украинского алфавита, передаются по телетайпу при помощи двух качественных признаков: наличия и отсутствия таковой посылки. Чему равно количество информации, приходящееся на одну принятую букву, на k принятых букв? Задача 5. Определить объем и количество информации при передаче русского текста из 350 букв при помощи пятизначного двоичного кода. Задача 6. Алфавит состоит из букв A,B,C,D. Вероятности появления буквы равны соответственно  ;  ;  . Определить количество информации на символ сообщения, составленного из такого алфавита.Задача 7. Определить объем и количество информации при следующих исходных условиях: А) алфавит  равновероятностный. Символы вторичного алфавита комбинируются в равномерные кодовые комбинации числом символов  .Б) первичный алфавит содержит 8 букв  . Буквы алфавита встречаются в сообщении с вероятностями:  ;  ;  ;  ;  .Кодовые комбинации во вторичном алфавите равномерные .В) первичные алфавит состоит из 5 букв  , которые встречаются с равными вероятностями в тексте, а и вторичные сообщения имеют одинаковую длину;Г) первичный алфавит равновероятный , а вторичные сообщения построены из кодовых комбинаций, имеющих среднюю длину 6 двоичных символов.Задача 8. На вычислительный центр с периферийного объекта необходимо передать определенную экономическую информацию, содержащуюся в таблицах с различными показателями. Определить максимально возможный объем информации, которым может быть загружен канал связи, если таблиц 100 шт., таблицы имеют 64 клетки, цифры, содержащиеся в таблицах не более, чем трехзначные, а код, в котором передаются сообщения – пятизначный двоичный. Задача 9. Рассмотрим некоторую ситуацию. В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Очевидно, вероятность того, что при вытаскивании "не глядя" попадется белый шар больше, чем вероятность попадания черного. Можно сделать заключение о вероятности события, которые интуитивно понятны. Провести количественную оценку вероятности для каждой ситуации. Задача 10. Ресурсы человеческого мозга позволяют обрабатывать информацию со скоростью около 16 бит/с. Какое количество информации перерабатывает человек в течение жизни (принять среднюю продолжительность жизни за 60 лет). Задача 11. Система имеет N равновероятных состояний. Количество информации в системе (о ее состоянии) равно 5 бит. Чему равна вероятность одного состояния? Если состояние системы неизвестно, то каково количество информации в системе? Если известно, что система находится в состоянии номер 8, то чему равно количество информации? Задача 12. Некоторая система может находиться в четырех состояниях с вероятностями: в первом (худшем) - 0,1, во втором и третьем (среднем) - 0,25, в четвертом (лучшем) - 0,4. Чему равно количество информации (неопределённость выбора) в системе? Задача 13. Чему равна энтропия системы, состоящей: А) из двух элементов, каждый из которых может с равной вероятностью находиться в двух состояниях? Б) из трех элементов, каждый из которых может с равной вероятностью находиться в четырех состояниях? Задача 14. Чему равна энтропия системы, состояние которой описывается дискретной величиной со следующим распределением вероятностей состояний
Задача 15. Чему равна энтропия сообщений: «Сейчас Луна упадет на Землю», «Сейчас Луна не упадет на Землю»? Задача 16. На вычислительном центре постоянная информация хранится в 32768 стандартных ячейках. Сколькими способами можно передать сведения о том, из какой ячейки необходимо извлечь информацию? Чему равно количество информации в каждом отдельном случае? Какое геометрическое расположение ячеек в хранилище позволит передавать эту информацию минимальным количеством качественных признаков? Задача 17. Генератор вырабатывает четыре частоты  . В шифраторе частоты комбинируются по три в кодовой комбинации. Определить:А) чему равно максимальное количество сообщений, составленных из этих частот Б) чему равно количество информации на один символ первичного алфавита? Вопросы для самоконтроля:
ЛАБОРАТОРНАЯ РАБОТА №3. «ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ» Цель: изучить позиционные системы счисления. Задачи:
Краткие теоретические сведения: В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа. В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q, иначе говоря, q единиц какого-либо разряда образуют единицу следующего разряда. Для записи чисел в q-ичной системе счисления требуется различных цифр (0, 1, …q-1). В позиционной системе счисления число в развернутой форме может быть представлено в следующем виде:  (1)где: А- само число; q — основание системы счисления; ai—цифры, принадлежащие алфавиту данной системе счисления; n — число целых разрядов числа; m — число дробных разрядов числа. Примером позиционной системы счисления является арабская десятичная система, в которой основание Р=10, для изображения используется 10 цифр от 0 до 9; Пример. Десятичное число  в развернутой форме запишется так: Существует множество позиционных систем счисления. Наиболее распространенные приведены в таблице:
В информатике нашли применение двоичная, восьмеричная, десятичная и шестнадцатеричная. Соответствие чисел в основных системах счисления Таблица 3.1
|
