Информатика и ИКТ лекция. Протокол умс от 201 г. Проректор по умр с. П. Ермишин
 Скачать 5.78 Mb. Скачать 5.78 Mb.
|
|
Задание 1. Найти значение приведенных ниже выражений; 1) х > у при а) х = 2, у = 2; б) х = 2, у = -8; 2) A OR B AND NOT С при А = False, B = True, С = False; 3) NOT (А< В) при а) A = 7, B= 9; б) А = 0, B = 2; 4) (x< у) OR (х = z) при а) х = 0, у = 0, z= 0; б) х = 0, у = -8, z = 0; 5) (а ≤ z) AND (z > 2) AND (а ≠5) при a) а = 2, z = 4; б) а = -5, z= 0; 6) A ≤ B при а) A = 2, B = 2; б) А = 2, В = -8; 7) А AND В OR NOT С при А = False, В = True, С = False; 8) NOT (х ≥ у) при а) х = 7, у = 9; б) х = 0, у = 2; 9) (x < у) AND (х = z) при а) х = 0, у = 0, z= 0; б) х = 0, у = -8, z = 0; 10) (а ≤ z) OR (z> 2) OR (а≠5) при а) а = 5, z= -4; б) а = -5, z = 0; Задание 2. По заданной логической схеме (рис.4.2) составить логическое выражение и выполнить для него таблицу истинности. 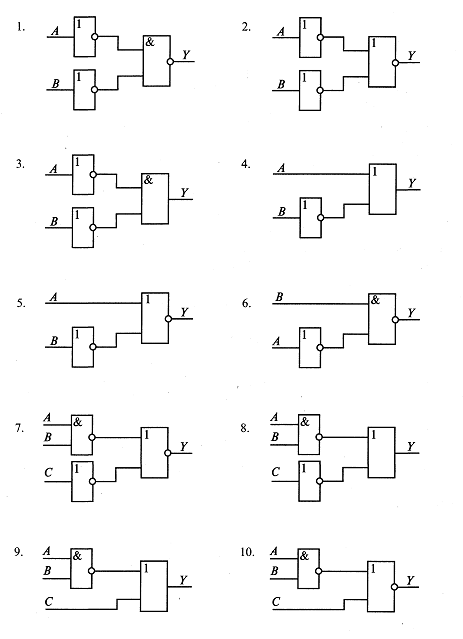 Рис. 8.2. Логические схемы Задание 3. По заданному логическому выражению составить логическую схему и построить таблицу истинности: 1. A AND B OR NOT С. 2. A AND NOT В OR С; 3. NOT (A AND NOT В) OR С 4. A OR NOT B AND C 5. A OR NOT (NOT B AND C); 6. NOT (A OR B) AND NOT C, 7. NOT(A AND B) OR NOT C, 8. NOT A OR В AND C, 9. NOT (NOT A OR В OR C); 10. NOT (NOT A OR B AND NOT C). Задание 4. Логические элементы И—HE и ИЛИ—НЕ называют базовыми, поскольку любой из перечисленных на рис. 4.1 логических элементов можно выразить только через И—НЕ (или ИЛИ—НЕ). Соответствующие схемы для одного из этих случаев приведены на рис. 8.3. 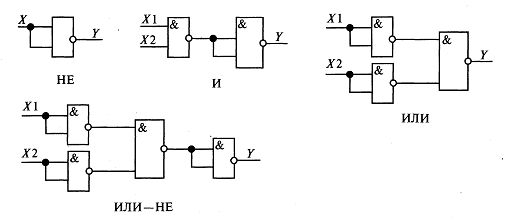 Рис.8.3 Реализация логических элементов через базовый И-НЕ Для того чтобы убедиться в справедливости сформулированного выше утверждения, достаточно перебрать вес возможные комбинации входных сигналов и найти результат. Покажем это на примере схемы для «И»; промежуточный результат обозначим через Z (табл. 8.2). Таблица 8.2.Реализация схемы «И»
Таким образом, сравнивая с табл. 8.1, убеждаемся в справедливости высказанного выше утверждения. Выполнить указанную проверку для всех схем на рис. 8.3. Разработать схемы реализации элементов НЕ, И, ИЛИ, И—НЕ через базовый логический элемент ИЛИ-НЕ. Задание 5. Кроме указанных выше одно- и двухвходовых элементов комбинационной логики, используют и более сложные — трех-, четырехвходовые и др., реализующие определенные логические функции более чем двух аргументов. Один из таких элементов изображен на рис. 8.4. (а); он реализует действие 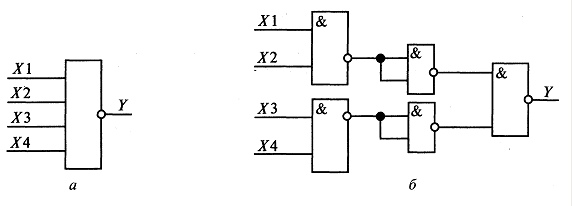 Рис. 8.4. Один из четырехвходовых элементов комбинационной лотки (а) и его реализация через двухвходовые элементы (б) Проверить, что четырехвходовый элемент, изображенный на рис. 8.4 (а), эквивалентен комбинации двухвходовых элементов, изображенной на рис. 8.4 ( б). Задание 6. Для сложения двух одноразрядных чисел применяется так называемый полусумматор, логическая схема которого изображена на рис. 4.5. Схема реализует арифметическое действие А+В =C0S, где А и В— одноразрядные двоичные числа, C0, и S-соответственно старший и младший двоичные разряды суммы (например, если А= 0 и В= 1, то С0 = 0 и S= 1). 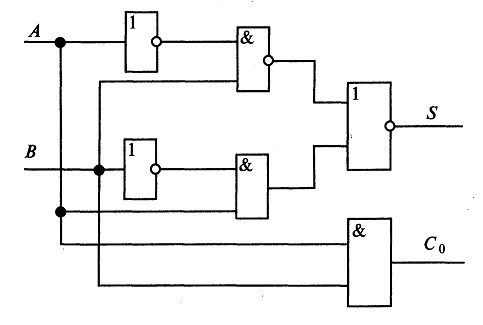 Рис. 8.5. Логическая схема полусумматора Проверить, что имеют место логические формулы: Примечание. Цифра «1» отождествляется с логическим «да» («истина», или 1), цифра «0» — с логическим «нет» («ложь», или 0). Задание 7. Для сложения двух двоичных разрядов А и В многоразрядного числа с учетом возможного добавления цифры Сi, оставшейся от сложения предыдущих разрядов используется так называемый одноразрядный сумматор. Пример. Складываем «столбиком» 1012 +1112. Для сложения крайних правых цифр достаточно использовать полусумматор; согласно обозначениям, принятым в задании 6, имеем: А=1, B=1 →C0 =0, S= 1. Продолжаем сложение теперь уже полусумматором не обойтись, т.к. надо фактически сложить три цифры: 0 и 1 (вторые справа разряды слагаемых) и 1, «пришедшую» из сложения предыдущих разрядов. Эта задача решается с помощью одноразрядного сумматора (рис. 8.6). 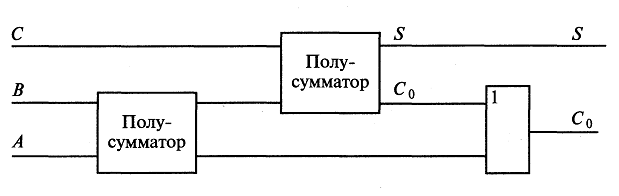 Рис. 8.6. Логическая схема одноразрядного сумматора. Проверить перебором всех возможных вариантов, что схема на рис. 8.6 действительно реализует указанное выше действие. Задание 8. Для сложения многоразрядных чисел используют устройства — сумматоры. Логическая схема трехразрядного сумматора приведена на рис. 8.7. 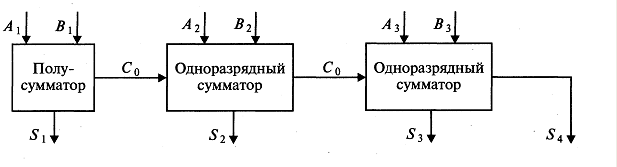 Рис. 8.7. Логическая схема трехразрядного сумматора Разобрать на примерах работу трехразрядного сумматора. Построить схему восьмиразрядного сумматора и разобрать его действие на примерах. Задание 9. Основное устройство последовательностной логики — триггер. На рис.8.8 —схема простейшего RS-триггера. R и S— входы, Qu 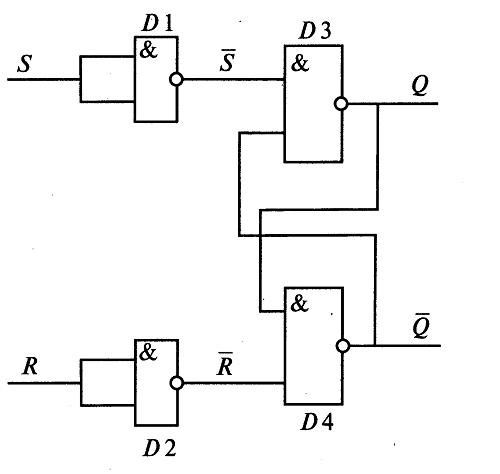 Рис. 8.8. Логическая схема RS-триггера Состояние на выходе триггера зависит не только от значений R и S на входе, но и от того, в каком состоянии находится триггер. Благодаря этому его можно использовать для записи и хранения информации (одного бита). Под действием входных сигналов триггер может переключаться из одного устойчивого состояния в другое. RS-триггер является асинхронным, поскольку информация в нем может изменяться в любой момент при изменении входных сигналов (в отличие от синхронизируемых триггеров, в которых информация на выходе может меняться только в определенные моменты времени). Вход S (Set) — вход установки триггера в единичное состояние, вход R (Reset) —сброса в нулевое состояние. Допустим, на входе S=1 и R= 0. Тогда на выходе будет Q= 1 и Отследить по схеме на рис. 8.8 справедливость сформулированного выше утверждения. Найти, каким будет состояние RS-триггера при входном сигнале R= 1 и S= 0 и каким оно станет после исчезновения сигнала. Проверить, что при входном сигнале S= 1, R= 1 оба выходных сигнала равны нулю, т.е. состояние системы не определено (в силу чего комбинация S= 1, R= 1 является запрещенной). Задание 9. Альтернативная схема RS-триггера на элементах И-НЕ имеет вид, изображенный на рис. 4.9 (входные сигналы Rи S при этом замешены на инверсные 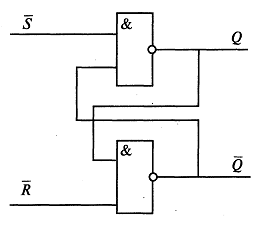 Рис. 8.9. Альтернативная схема RS-триггера. Проанализировать работу RS-триггера, основанного на схеме рис. 4.9. Подтвердить, что утверждения табл. 8.3 верны. Таблица 8.3. Таблица истинности для RS-триггера
Найти в литературе логическую схему одного из синхронных (синхронизируемых) триггеров и разобрать его работу. Сконструируйте устройство, собранное только из базовых двухвходных элементов И—НЕ, реализующее операцию: а) НЕ; б) И; в) ИЛИ; г) ИЛИ—НЕ; д) И—ИЛИ—НЕ (NOT (A AND В OR С AND D)); е) сложения по модулю два (NOT (NOT A AND В) OR NOT (C AND D))). Вопросы для самоконтроля 1. Назовите основные логические операции и приведите их таблицы истинности. 2. Что такое логическое выражение? 3. Каков порядок выполнения операций при вычислении значения логического выражения? 4. Приведите примеры логических выражений и вычисления их значений. 5. Назовите элементарные логические элементы и приведите их обозначения на схемах. 6. Изобразите электрические схемы, реализующие элементарные логические элементы. 7. Приведите примеры построения схем на логических элементах на основе логического выражения. 8. Приведите примеры построения логических выражений по заданным логическим схемам. 9. Что такое триггер? Перечислите виды триггеров и коротко их охарактеризуйте. 10. Чем отличается синхронный триггер от несинхронного? 11. Проиллюстрируйте на примерах хранение информации в триггере и запись нуля или единицы. 12. Какое состояние триггера называют недопустимым? 13. Расскажите об элементе «Исключающее ИЛИ», приведите таблицу истинности для соответствующей логической операции. 14. Расскажите о полусумматоре. 15. Расскажите о сумматоре и организации переноса «запасного» разряда. ЛАБОРАТОРНАЯ РАБОТА №9. «Основы работы с MathCAD» Цель: изучить основы вычисления в MathCad. Задачи:
Краткая теория по теме: Mathcad работает с документами. С точки зрения пользователя, документ - это чистый лист бумаги, на котором можно размещать области трех основных типов: математические выражения, текстовые фрагменты и графические области. Математические выражения К основным элементам математических выражений Mathcad относятся типы данных, операторы, функции и управляющие структуры. Типы данных К типам данных относятся числовые константы, обычные и системные переменные, массивы (векторы и матрицы) и данные файлового типа. Константами называют поименованные объекты, хранящие некоторые значения, которые не могут быть изменены. Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Имена констант, переменных и иных объектов называют идентификаторами. Идентификаторы в Mathcad представляют собой набор латинских или греческих букв и цифр. В Mathcad содержится небольшая группа особых объектов, которые нельзя отнести ни к классу констант, ни к классу переменных, значения которых определены сразу после запуска программы. Их правильнее считать системными переменными, имеющими предопределенные системой начальные значения. Обычные переменные отличаются от системных тем, что они должны быть предварительно определены пользователем, т. е. им необходимо хотя бы однажды присвоить значение. В качестве оператора присваивания используется знак “:=”, тогда как знак “=” отведен для вывода значения константы или переменной. 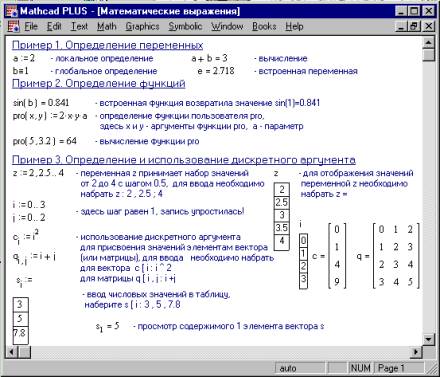 Рис. 9.1. Математические выражения Если переменной присваивается начальное значение с помощью оператора :=, такое присваивание называется локальным. До этого присваивания переменная не определена и ее нельзя использовать. Однако с помощью знака можно обеспечить глобальное присваивание (см. Пример 1 Рис. 9.1). Существует также жирный знак равенства, который используется, например, как оператор приближенного равенства при решении систем уравнений. Операторы Операторы - элементы Mathcad, с помощью которых можно создавать математические выражения. К ним, например относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д. После указания операндов (параметров операторов) операторы становятся исполняемыми по документу блоками, например, 2 + 5 -оператор сложения с двумя операндами. В Приложении 2 данного пособия приведен список наиболее часто используемых операторов. Функции В пакете Mathcad имеется множество встроенных функций, т.е. функций, заблаговременно введенных разработчиками (см. Приложение 3). Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение. Важной особенностью пакета является возможность задания внешних функций, или функций пользователя. Следует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции (см. Пример 2 Рис. 9.1). Дискретные аргументы Дискретные аргументы - особый класс переменных, который в пакете Mathcad зачастую заменяет управляющие структуры, называемые циклами (однако полноценной такая замена не является). Эти переменные имеют ряд фиксированных значений, либо целочисленных, либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного. Дискретные аргументы значительно расширяют возможности Mathcad, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы (Пример 3 Рис. 9.1). Массивы Массив - имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете Mathcad используются массивы двух наиболее распространенных типов: одномерные (векторы) и двумерные (матрицы). Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или единицы, в соответствии со значением системной переменной ORIGIN. Векторы и матрицы можно задавать различными способами:
Текстовые фрагменты Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов - текстовая область (region) и текстовый диапазон (band). Текстовые области предназначены для небольших кусков текста - подписей, комментариев и т.п. Текстовые диапазоны применяются в том случае, если необходимо работать с абзацами или страницами. Графические области Графические области делятся на три основных типа - двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим Mathcad на основании обработанных данных. FRAME_._Выберите_Windows->Animation->Create'>FRAME'>Создание анимационного клипа Mathcad имеет встроенную переменную FRAME, чье единственное назначение - управление анимациями:
Сообщения об ошибках При выполнении вычислений возможны ошибки. Сообщение об ошибке в Mathcad выводится в красном прямоугольнике, от которого отходит линия, указывающая на место ошибки. В Приложении 4 приведен список сообщений об ошибках. Порядок выполнения лабораторной работы: |
