Информатика и ИКТ лекция. Протокол умс от 201 г. Проректор по умр с. П. Ермишин
 Скачать 5.78 Mb. Скачать 5.78 Mb.
|
|
Вопросы для самоконтроля:
 Рис. 9.8 – Результаты вычисления матриц ЛАБОРАТОРНАЯ РАБОТА №10. «ИНФОРМАЦИОННАЯ БЕЗОПАСНОСТЬ. ОСНОВЫ КРИПТОГРАФИИ» Цель: ознакомиться с основами криптографии. Изучить виды шифрования. Задачи:
Краткая теория по теме: Один из методов защиты информации от неправомерного доступа — это шифрование, то есть кодирование специального вида. Шифрование — это преобразование (кодирование) открытой информации в зашифрованную, недоступную для понимания посторонних. Шифрование применяется в первую очередь для передачи секретной информации по незащищенным каналам связи. Шифровать можно любую информацию — тексты, рисунки, звук, базы данных и т.д. Человечество применяет шифрование с того момента, как появилась секретная информация, которую нужно было скрыть от врагов. Первое известное науке шифрованное сообщение — египетский текст, в котором вместо принятых тогда иероглифов были использованы другие знаки. Методы шифрования и расшифровывания сообщения изучает наука криптология, история которой насчитывает около четырех тысяч лет. Она состоит из двух ветвей: криптографии и криптоанализа. Криптография –это наука о способах шифрования информации. Критоанализ –это наука о методах и способах вскрытия шифров. Обычно предполагается, что сам алгоритм шифрования известен всем, но неизвестен его ключ, без которого сообщение невозможно расшифровать. В этом заключается отличие шифрования от простого кодирования, при котором для восстановления сообщения достаточно знать только алгоритм кодирования. Ключ — это параметр алгоритма шифрования (шифра), позволяющий выбрать одно конкретное преобразование из всех вариантов, предусмотренных алгоритмом. Знание ключа позволяет свободно зашифровывать и расшифровывать сообщения. Все шифры (системы шифрования) делятся на две группы — симметричные и несимметричные (с открытым ключом). Симметричный шифр означает, что и для шифрования, и для расшифровывания сообщений используется один и тот же ключ. В системах с открытым ключом используются два ключа — открытый и закрытый, которые связаны друг с другом с помощью некоторых математических зависимостей. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения. Криптостойкость шифра — это устойчивость шифра к расшифровке без знания ключа. Стойким считается алгоритм, который для успешного раскрытия требует от противника недостижимых вычислительных ресурсов, недостижимого объема перехваченных сообщений или такого времени, что по его истечении защищенная информация будет уже неактуальна. Шифр Цезаря (назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки.)— один из самых известных и самых древних шифров. В этом шифре каждая буква заменяется на другую, расположенную в алфавите на заданное число позиций k вправо от нее. Алфавит замыкается в кольцо, так что последние символы заменяются на первые. Вот пример шифра Цезаря (со сдвигом 3): 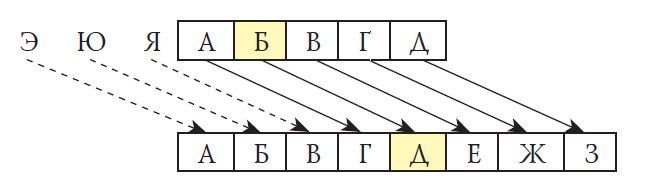 Знаменитая фраза "ПРИШЕЛ УВИДЕЛ ПОБЕДИЛ" при использовании шифра Цезаря со сдвигом 3 будет закодирована так: тулыио ЦЕЛЗИО ТСДИЗЛО Если первая буква алфавита имеет код 0, вторая — код 1 и т.д., алгоритм шифрования может быть выражен формулой у = (x + k) mod n, где x — код исходного символа, k — величина сдвига, у — код символа-замены, n — количество символов в алфавите, а запись (x + k) mod n обозначает остаток от деления x + k на n. Операция взятия остатка от деления необходима для того, чтобы "замкнуть" алфавит в кольцо. Например, при использовании русского алфавита (32 буквы, будем считать, что буквы Е и Ё совпадают.) для буквы "Я" (код 31) получаем код заменяющего символа (31 + 3) mod 32 = 2, это буква "В". Ключом для шифра Цезаря служит сдвиг k; если его знать, то сообщение легко расшифровать. Для этого используется формула х = (y - k + n) mod n. Шифр Цезаря относится к шифрам простой подстановки, так как каждый символ исходного сообщения заменяется на другой символ из того же алфавита. Такие шифры легко раскрываются с помощью частотного анализа, потому что в каждом языке частоты встречаемости букв примерно постоянны для любого достаточно большого текста. Значительно сложнее сломать шифр Виженера (назван по имени Блеза Виженера, швейцарского дипломата XVI века.), который стал естественным развитием шифра Цезаря. Для использования шифра Виженера используется ключевое слово, которое задает переменную величину сдвига. Например, пусть ключевое слово — "ЗАБЕГ". По таблице определяем коды букв: 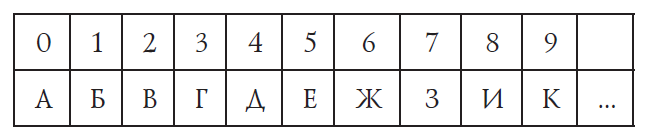 Получаем: "З" - 7, "А" - 0, "Б" - 1, "Е" - 5, "Г" - 3. Это значит, что для кодирования первой буквы используется сдвиг 7, для кодирования второй — 0 (символ не меняется) и т.д. Для пятой буквы используется сдвиг 3, а для шестой — снова 7 (начали "проходить" кодовое слово сначала). Фраза "ПРИШЕЛ УВИДЕЛ ПОБЕДИЛ" при использовании шифра Виженера с ключом "ЗАБЕГ" будет закодирована в виде "ЦРЙЭИТ ФЗЛЛЕМ ТХБЖЙЛТ". Шифр Виженера обладает значительно более высокой криптостойкостью, чем шифр Цезаря. Это значит, что его труднее раскрыть — подобрать нужное ключевое слово. Теоретически, если длина ключа равна длине сообщения и каждый ключ используется только один раз, шифр Виженера взломать невозможно. Задания для выполнения 1. Зашифруйте с помощью шифра Цезаря со сдвигом 6 высказывание "ЛЮДИ ОХОТНО ВЕРЯТ ТОМУ, ЧЕМУ ЖЕЛАЮТ ВЕРИТЬ". 2. Напишите программу, которая выполняет шифрование строки с помощью шифра Цезаря. 3. Попытайтесь расшифровать сообщение, закодированное шифром Цезаря с неизвестным сдвигом:"ХШЖНПУТ ФКХКОЙКТ". Для этого можно написать программу. 4. Используя шифр Виженера с ключом "ЛЕНА", зашифруйте сообщение "НЕЛЬЗЯ ОБИЖАТЬ ГОСТЯ". 5. Измените программу для шифрования Цезаря так, чтобы учитывать букву Ё. 6. Измените программу для шифрования Цезаря так, чтобы учитывать и букву Ё, и пробел. Современные алгоритмы шифрования Государственным стандартом шифрования в России является алгоритм, зарегистрированный как ГОСТ 28147-89. Он является блочным шифром, то есть шифрует не отдельные символы, а 64-битные блоки. В алгоритме предусмотрено 32 цикла преобразования данных с 256-битным ключом, за счет этого он очень надежен (обладает высокой криптостойкостью). На современных компьютерах раскрытие этого шифра путем перебора ключей ("методом грубой силы") займет не менее сотен лет, что делает такую атаку бессмысленной. В США используется аналогичный блочный шифр AES. В Интернете популярен алгоритм RSA, названный так по начальным буквам фамилий его авторов — Р.Райвеста (R.Rivest), А.Шамира (A.Shamir) и Л.Адлемана (L.Adleman). Это алгоритм с открытым ключом, стойкость которого основана на использовании свойств простых чисел. Для его взлома нужно разложить очень большое число на простые сомножители. Эту задачу сейчас умеют решать только перебором вариантов. Поскольку количество вариантов огромно, для раскрытия шифра требуется много лет работы современных компьютеров. Для применения алгоритма RSA требуется построить открытый и секретный ключи следующим образом. 1. Выбрать два больших простых числа, p и q. 2. Найти их произведение n = p • q и значение 3. Выбрать число e (1 < e < 4. Найти число d, которое удовлетворяет условию d • е = k 5. Пара значений (e, n) — это открытый ключ RSA (его можно свободно публиковать), а пара (d, n) — это секретный ключ. Передаваемое сообщение нужно сначала представить в виде последовательности чисел в интервале от 0 до n -1. Для шифрования используют формулу у = xemod n, где x — число исходного сообщения, (e, n) — открытый ключ, y — число закодированного сообщения, а запись xe mod n обозначает остаток от деления xe на n. Расшифровка сообщения выполняется по формуле х = yd mod n. Это значит, что зашифровать сообщение может каждый (открытый ключ общеизвестен), а прочитать его — только тот, кто знает секретный показатель степени d. Пример. Работа алгоритма RSA Возьмем p = 3 и q = 7, тогда находим n = pq = 21 и = (р - 1) • (q - 1) = 12. Выберем e = 5, тогда равенство d • e = к + 1 выполняется, например, при d = 17 ( и k = 7). Таким образом, мы получили открытый ключ (5, 21) и секретный ключ (17, 21). Зашифруем сообщение "123" с помощью открытого ключа (5,21). Получаем 1=> 15 mod 21 = 1, 2=> 25 mod 21 =11, 3=>35mod21 = 12, то есть зашифрованное сообщение состоит из чисел 1, 11 и 12. Зная секретный ключ (17, 21), можно его расшифровать: 1=> 117 mod 21 = 1, 11=> 1117 mod 21 =2, 12 => 1217 mod 21 = 3. Мы получили исходное сообщение. Конечно, вы заметили, что при шифровании и расшифровке приходится вычислять остаток от деления очень больших чисел (например, 1217) на n. Оказывается, само число 1217 в этом случае находить не нужно. Достаточно записать в обычную целочисленную переменную, например x, единицу, а потом 17 раз выполнить преобразование х = 12х mod 21. После этого в переменной x будет значение 1217 mod 21 = 3. Попробуйте доказать правильность этого алгоритма. Для того чтобы расшифровать сообщение, нужно знать секретный показатель степени d. А для этого, в свою очередь, нужно найти сомножители p и q, такие что n = р - q. Если n велико, это очень сложная задача, ее решение перебором вариантов на современном компьютере займет сотни лет. В 2009 году группа ученых из разных стран в результате многомесячных расчетов на сотнях компьютеров смогла расшифровать сообщение, зашифрованное алгоритмом RSA с 768-битным ключом. Поэтому сейчас надежными считаются ключи с длиной 1024 бита и более. Если будет построен работающий квантовый компьютер, взлом алгоритма RSA будет возможен за очень небольшое время. При использовании симметричных шифров всегда возникает проблема: как передать ключ, если канал связи ненадежный? Ведь, получив ключ, противник сможет расшифровать все дальнейшие сообщения. Для алгоритма RSA этой проблемы нет, сторонам достаточно обменяться открытыми ключами, которые можно показывать всем желающим. У алгоритма RSA есть еще одно достоинство: его можно использовать для цифровой подписи сообщений. Она служит для доказательства авторства документов, защиты сообщений от подделки и умышленных изменений. Цифровая подпись — это набор символов, который получен в результате шифрования сообщения с помощью личного секретного кода отправителя. Отправитель может передать вместе с исходным сообщением такое же сообщение, зашифрованное с помощью своего секретного ключа (это и есть цифровая подпись). Получатель расшифровывает цифровую подпись с помощью открытого ключа. Если она совпала с незашифрованным сообщением, можно быть уверенным, что его отправил тот человек, который знает секретный код. Если сообщение было изменено при передаче, оно не совпадет с расшифрованной цифровой подписью. Так как сообщение может быть очень длинным, для сокращения объема передаваемых данных чаще всего шифруется не все сообщение, а только его хэш-код. Во многих современных программах есть возможность шифровать данные с паролем. Например, офисные пакеты OpenOffice.org и Microsoft Office позволяют шифровать все создаваемые документы (для их просмотра и/или изменения нужно ввести пароль). При создании архива (например, в архиваторах WinRAR, WinZip) также можно установить пароль, без которого извлечь файлы невозможно. В простейших задачах для шифрования файлов можно использовать бесплатную программу Шифровальщик (www.familytree.ru/ru/cipher.htm), версии которой существуют для Linux и Windows. Программы TrueCrypt (www.truecrypt.org), BestCrypt (www. jetico.com) и FreeOTFE (freeotfe.org) создают логические диски-контейнеры, информация на которых шифруется. Свободно распространяемая программа DiskCryptor (diskcryptor.net) позволяет шифровать разделы жестких дисков и даже создавать шифрованные флэш-диски и CD/DVD-диски. Программа GnuPG (gnupg.org) также относится к свободному программному обеспечению. В ней поддерживаются симметричные и несимметричные шифры, а также различные алгоритмы электронной цифровой подписи. Задания для выполнения 1. Напишите программу, которая строит открытый и секретный ключи RSA для небольших множителей p и q. 2. Напишите программу, которая шифрует и расшифровывает сообщения с помощью алгоритма при небольших значениях открытого и секретного ключей. Вопросы для самоконтроля: 1. Чем отличаются понятия "шифрование" и "кодирование"? 2. Что такое ключ? 3. Как называется наука, изучающая методы шифрования? 4. Что такое симметричный шифр? Какая проблема возникает при использовании симметричного шифра, если участники переписки находятся в разных странах? 5. Что такое несимметричные шифры? На чем основана их надежность? 6. Что такое криптостойкость алгоритма? Какой алгоритм считается криптостойким? 7. Какой алгоритм шифрования принят в России в качестве государственного стандарта? 8. Что такое блочный алгоритм шифрования? 9. К какому типу относится алгоритм RSA? На чем основана его криптостойкость? 10. Что такое цифровая подпись? 11. Как можно использовать алгоритм RSA для цифровой подписи? ЛАБОРАТОРНАЯ РАБОТА №11. «Создание одноранговой сети» Цель: научиться создавать одноранговые сети при использовании топологии сети с шиной типа «звезда».. Задачи:
Пошаговое создание сети: Р  ис. 11.1 1. Для всех компьютеров присоедините сетевые адаптеры рабочих станций, входящих в рабочую группу, к хабу рабочей группы, используя кабель пятой категории с RJ-45 коннекторами. 2. Запустите те компьютеры, которые будут объединены в индивидуальные рабочие группы. Для того, чтобы начать создание одноранговой сети для рабочей группы, запустите «Мастер настройки сети», выполните следующие действия на одном компьютере каждой сети: 3. Щелкните Пуск, затем щелкните Панель управления. 4. Щелкните Сетевые подключения, а затем на правой панели щелкните Установить домашнюю сеть или сеть малого офиса. 5. На странице Мастер настройки сети щелкните Далее.  Рис. 11.2 6. На следующей странице просмотрите требования и, убедившись, что все соответствует, щелкните Далее.  Рис. 11.3 7. На странице Выберите метод подключения щелкните Другое и затем щелкните Далее. 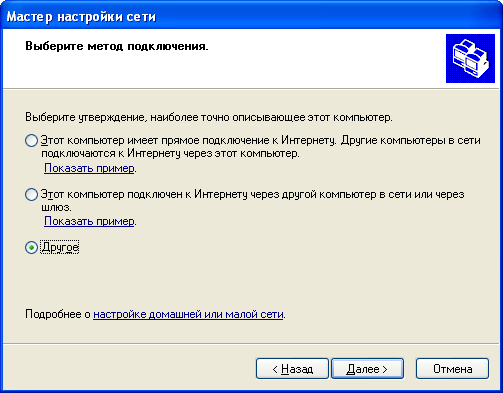 Рис. 11.4 8. На странице Другие способы подключения к Интернету щелкните Этот компьютер принадлежит к сети, не имеющей подключения к Интернету, затем щелкните Далее. 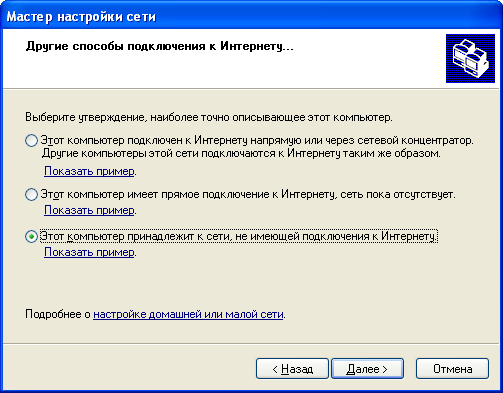 Рис. 11.5 9. В текстовое поле Описание введите workstation. 10. В текстовое поле Имя компьютера введите уникальное имя (например: STUDENTA), называя тем самым свою рабочую станцию в сети, а затем щелкните Далее. Замечание: Когда вы даете имя своему компьютеру, убедитесь, что это имя уникально в данной рабочей группе. Именуйте компьютеры последовательно, например, StudentB, StudentC, StudentD и так далее. 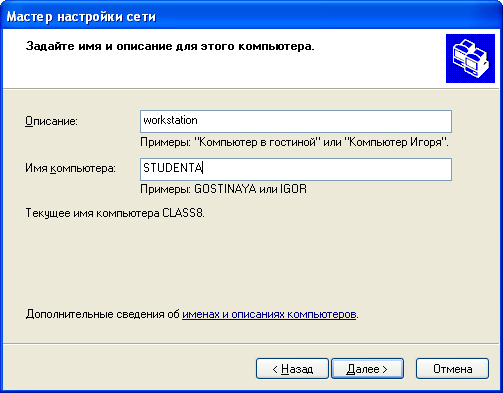 Рис. 11.6 11. На странице Задайте имя для вашей сети смените стандартное имя Рабочей группы на MYNETWORK. 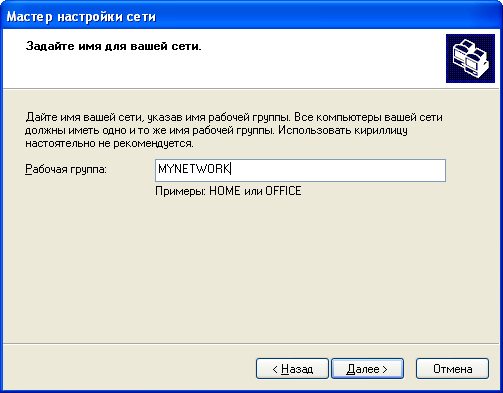 Рис. 11.7 12. На странице Все готово для применения сетевых параметров проверьте установки и затем щелкните Далее для того, чтобы начать процесс создания сетевого соединения. 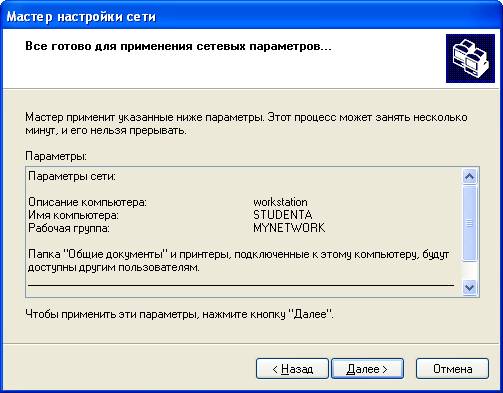 Рис. 11.8 13. На следующей странице щелкните Просто завершить работу мастера, а затем щелкните Далее. 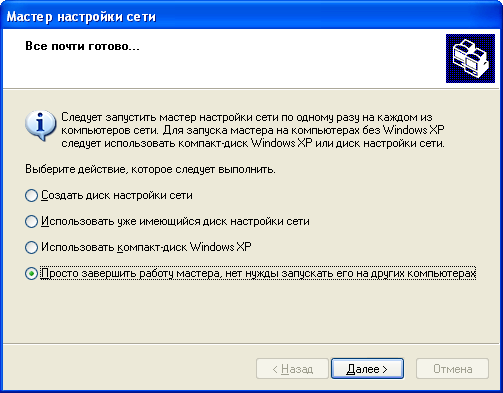 Рис. 11.9 14. На странице Завершение работы мастера настройки сети щелкните Готово. 15. Если вам будет предложено перезагрузить ваш компьютер, то щелкните Да. 16. Начните работу на своем компьютере. 17. Запустите «Мастер настройки сети» (шаги с 3 по 13) на остальных компьютерах в каждой сети, чтобы подключить их к рабочей группе MYNETWORK Для проверки работы одноранговой сети создайте папку для совместного использования на каждом компьютере. Выполните следующие действия на каждом компьютере. 18. Щелкните Пуск, отметьте Все программы, щелкните Стандартные, и затем щелкните Проводник. 19. На левой панели щелкните Мои документы в открывшемся окне щелкните Файл, затем отметьте Создать, и щелкните Папка. 21. Введите Имя папки, которое состоит из вашего имени и слова Папка (например: Папка Глеба), и нажмите Enter. 22. В окне Мои документы щелкните правой кнопкой мыши по только что созданной папке и выберите пункт меню Общий доступ и безопасность. 23. Во вкладке Доступ щелкните Открыть общий доступ к этой папке- OK. 24. В правой половине открывшегося окна дважды щелкните по только что созданной папке. 25. В открывшемся окне щелкните Файл, отметьте Создать и щелкните Текстовый документ. 26. Введите имя документа (используйте ваше имя для названия файла) и нажмите Enter. 27. Дождитесь, пока остальные студенты создадут файлы в директории для совместного использования. Для доступа учащихся к совместно используемым файлам, созданным на других компьютерах, необходимо следовать указаниям: 28. Щелкните Пуск, отметьте Все программы, щелкните Стандартные, а затем щелкните на Проводник. 29. На левой панели щелкните Сетевое окружение, а затем щелкните Отобразить компьютеры рабочей группы. Замечание: теперь вы можете увидеть список компьютеров рабочей группы сети MYNETWORK. 30. На правой панели дважды щелкните по какому-либо компьютеру (не своему) для того, чтобы найти файлы, созданные другими учащимися для совместного пользования. 31. На правой панели дважды щелкните по одной из созданных папок для получения доступа к файлам, созданным другими учащимися. 32. На правой панели дважды щелкните по имени файла, чтобы открыть его. Итак, ,вы получили удаленный доступ к файлам на другом компьютере. Требования к оформлению и защите лабораторных работ По каждой лабораторной работе оформляется отчет, который предоставляется преподавателю для защиты не позднее следующего лабораторного занятия. К защите лабораторной работы студент должен подготовить ответы на вопросы для самоконтроля. Все лабораторные работы с подписью преподавателя оформляются в журнал отчетов по лабораторным работам. Требования к оформлению журнала и лабораторных работ представлены ниже:
При указании источников данных, используемой литературы необходимо оформлять библиографический список в соответствии с ГОСТ. |
