Информатика и ИКТ лекция. Протокол умс от 201 г. Проректор по умр с. П. Ермишин
 Скачать 5.78 Mb.
|
|
Задание 1. Вычислить:  , |-10| = , 10! = .Это и все остальные задания снабдить комментариями, используя команды Text → Create Text Region или Text→Create Text Paragraph. Задание 2.Определить переменные: a := 3.4, b := 6.22, c:=0.149 (причем переменную с - глобально) и выражения:  ,  .
Задание 3.Вывести на экран значение системной константы π и установить максимальный формат ее отображения локально. Задание 4.Выполнить следующие операции с комплексными числами: Z:= -3 + 2i, |Z| = , Re(Z)= , Im(Z)= , arg(Z)= ,  , =,2Z = ,Z1:=1+2i, Z2:=3+4i, Z1+Z2= , Z1- Z2= , Z1 Z2= , Z1/Z2 = . Задание 5.Выполнить следующие операции:  ,  ,  ,  , x:=2,  Задание 6. Определить векторы d, S и R через дискретный аргумент i. Отобразить графически таблично заданные функции Ri(di) и Si(di),используя команду Graphics→Create X-Y Plot. 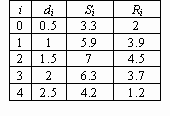 Введем: i:=0,1…4. Ввод числовых значений в таблицу наберите di:=0.5, 1, 1.5,2, 2.5 Чтобы оформить график, необходимо выполнить следующие команды:
Задание 7.Построить декартовые (X-Y Plot) и полярные (Polar Plot) графики следующих функций:    Для этого необходимо определить а как дискретный аргумент на интервале от 0 до 2π с шагом  π/30.Определить по графику X-Y Plot координаты любой из точек пересечения графиков Y(a ) иP(a ), для этого необходимо:
Вычислить значения функций Х(a) и Y(a) при a :=π/ 2. Задание 8.Используя командуMath→Matricsсоздать матрицу Qразмером 6 на 6, заполнить ее произвольно и отобразить графически с помощью команды Graphics-Create Surface Plot. Задание 9. Нахождение корней уравнения в программе MathCad с использованием встроенной функции root. 1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни (индивидуальные варианты см. таблицу 1). 2. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х). 3. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения. 3.1. Использовать для определения на графике значений корней в контекстном меню (рис.9.2, a) опцию Trace (Рис. 9.2,б), установить флажок в окне Track Data Poіnt. 3.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая. 4. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1. 5. Найти второй (х2) и третий (х3) корень уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root. 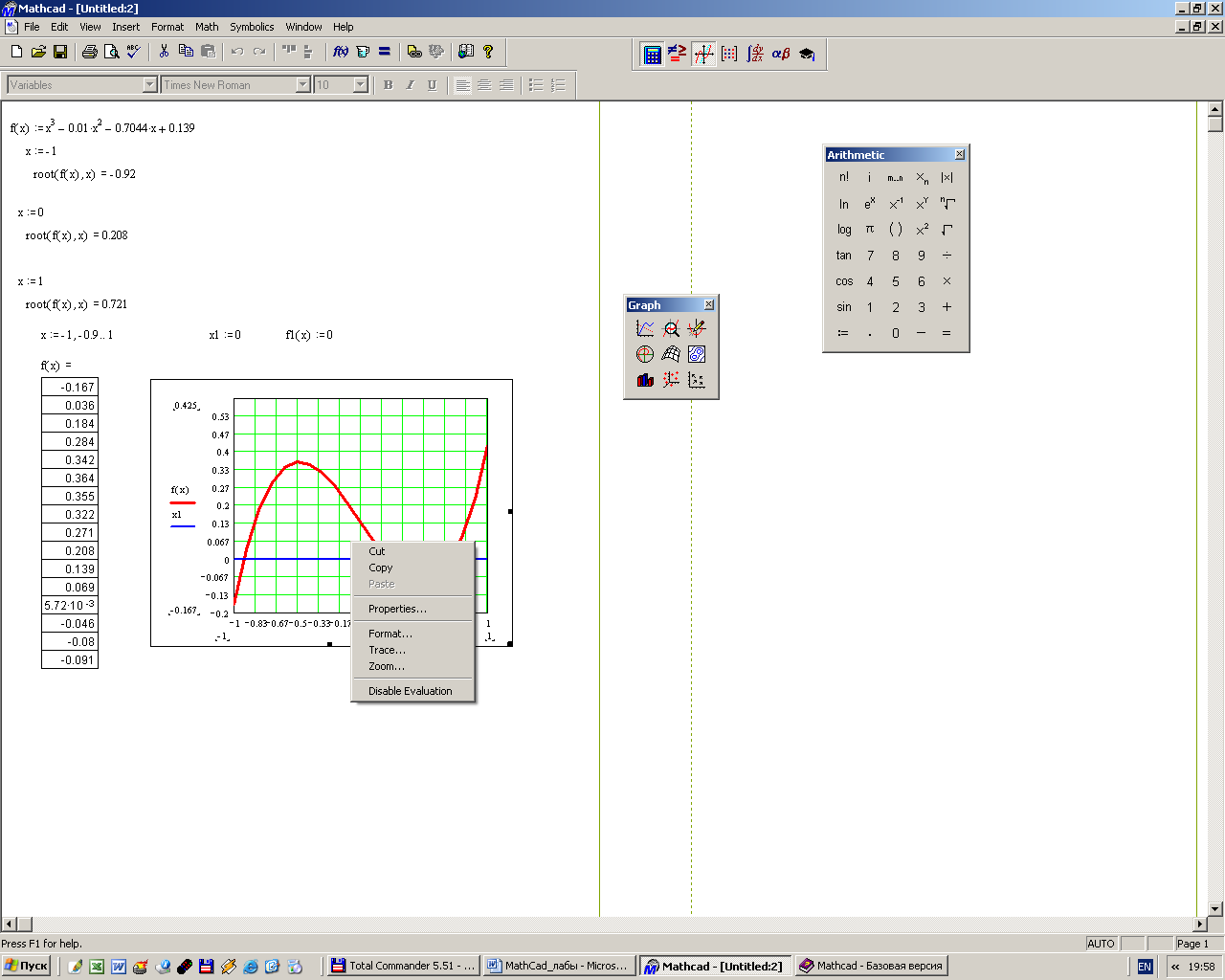  а) б) Рис. 9.2 – Диалоговые окна для определения координат точек пересечения кривых Пример. Для уравнения  найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.1 Записать цикл из точек интервала х:=-1, -0.9..1. 2 Записать функции  и х0=0.3 Построить графики для этих функций. 4. Определить на графике точки пересечения кривых и х0=0.5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7. 6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (Рис. 9.3). 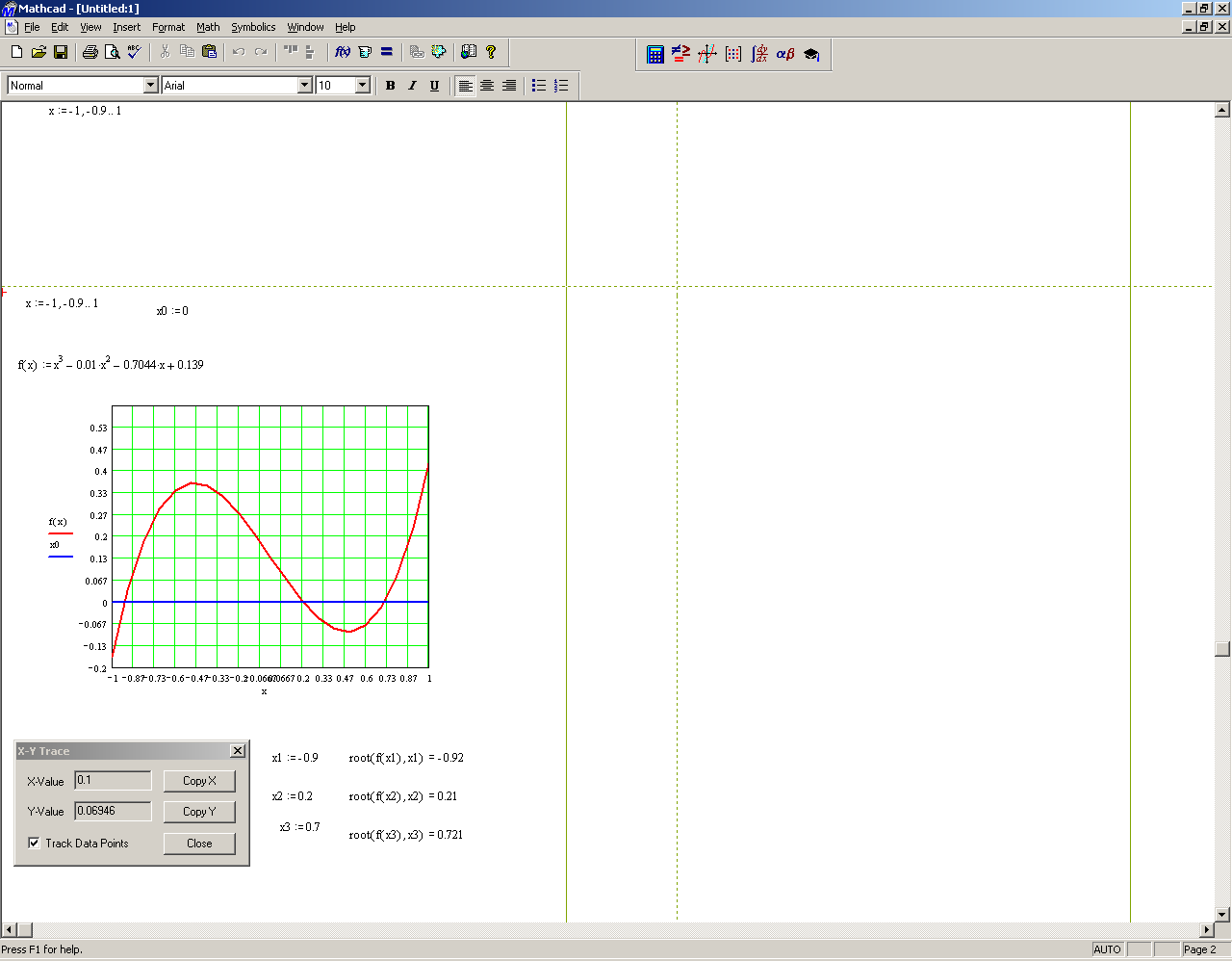 Рис. 9.3 – Результат нахождения корней с использованием функции root Задание 10. Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором. 1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни. 2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней. 3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора rT. 4. Для интервала нахождения корня и количества элементов вектора rT создать соответствующие циклы и вычислить значение функции в точках цикла. 5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю. Пример. Для уравнения  найти корни на интервале [-1.1, 7.1] , шаг изменения переменной х равен 0.1.1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.9.4) и задав один столбец и четыре строки для коэффициентов уравнения. 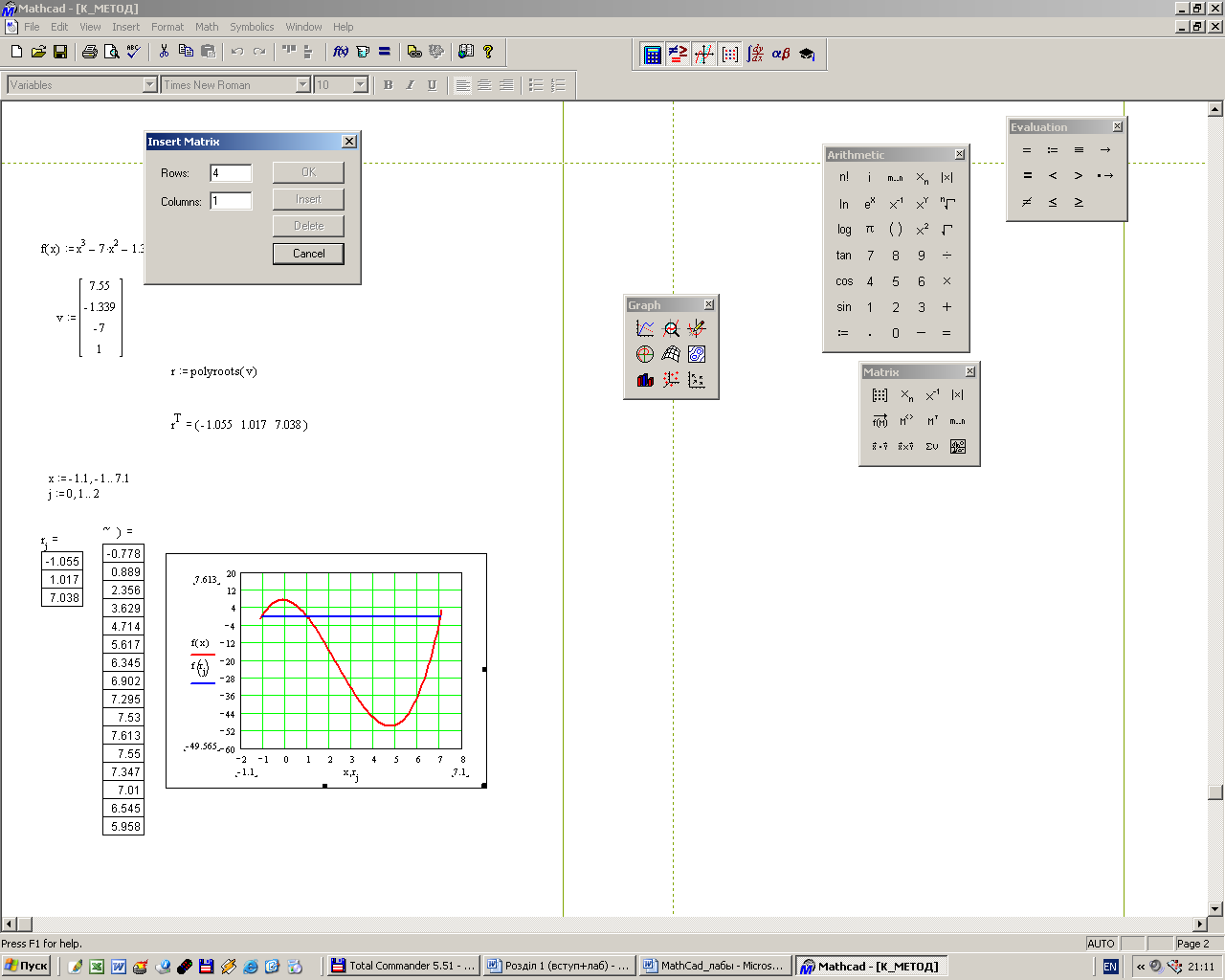 Рис. 9.4 – Диалоговое окно для определения вектора из коэффициентов уравнения Вектор из коэффициентов уравнения будет иметь следующий вид 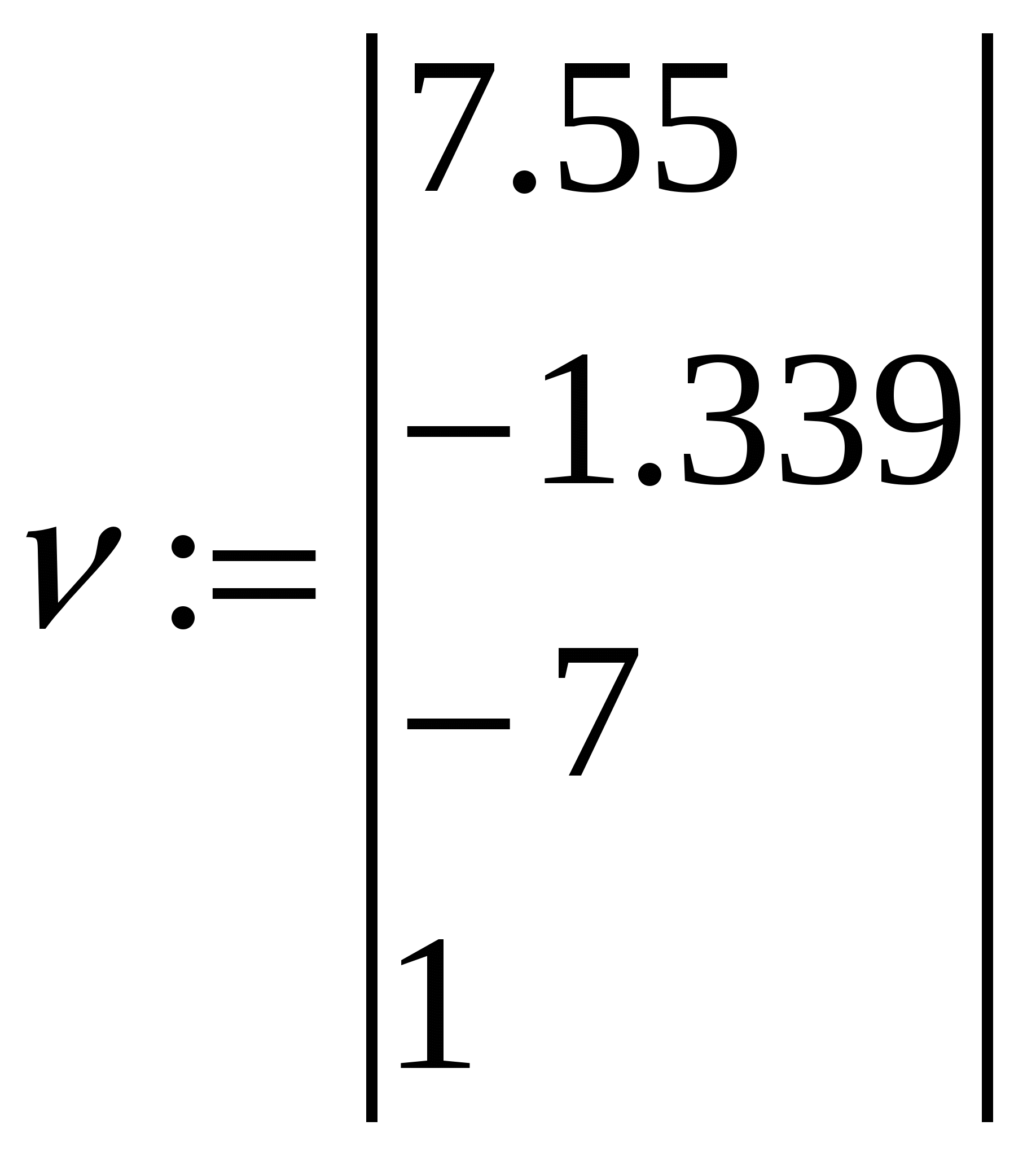 2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора rT, транспонированного по отношению к r, то есть преобразованного из столбца в строку. 3. Создать циклы для переменной х и количества найденных корней: 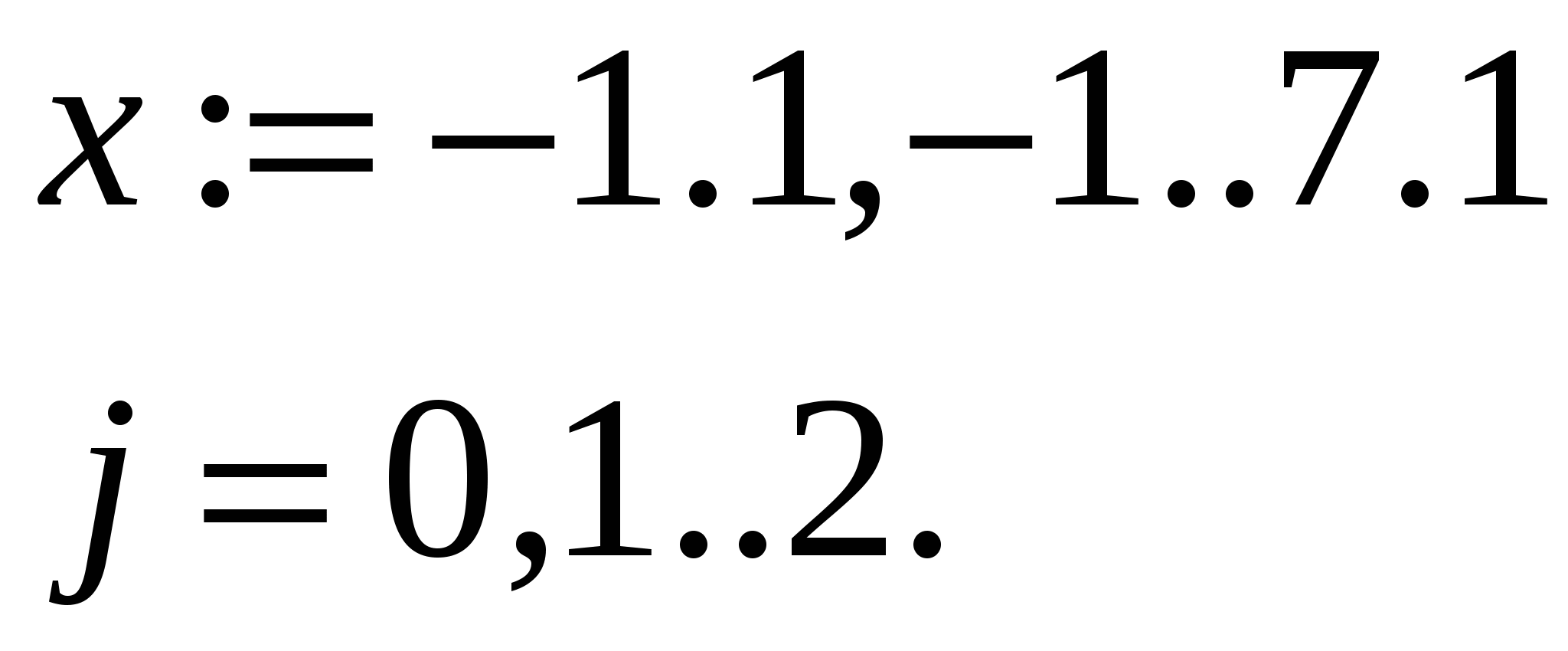 4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю. 5. Определить значения корней на графике (Рис. 9.5). 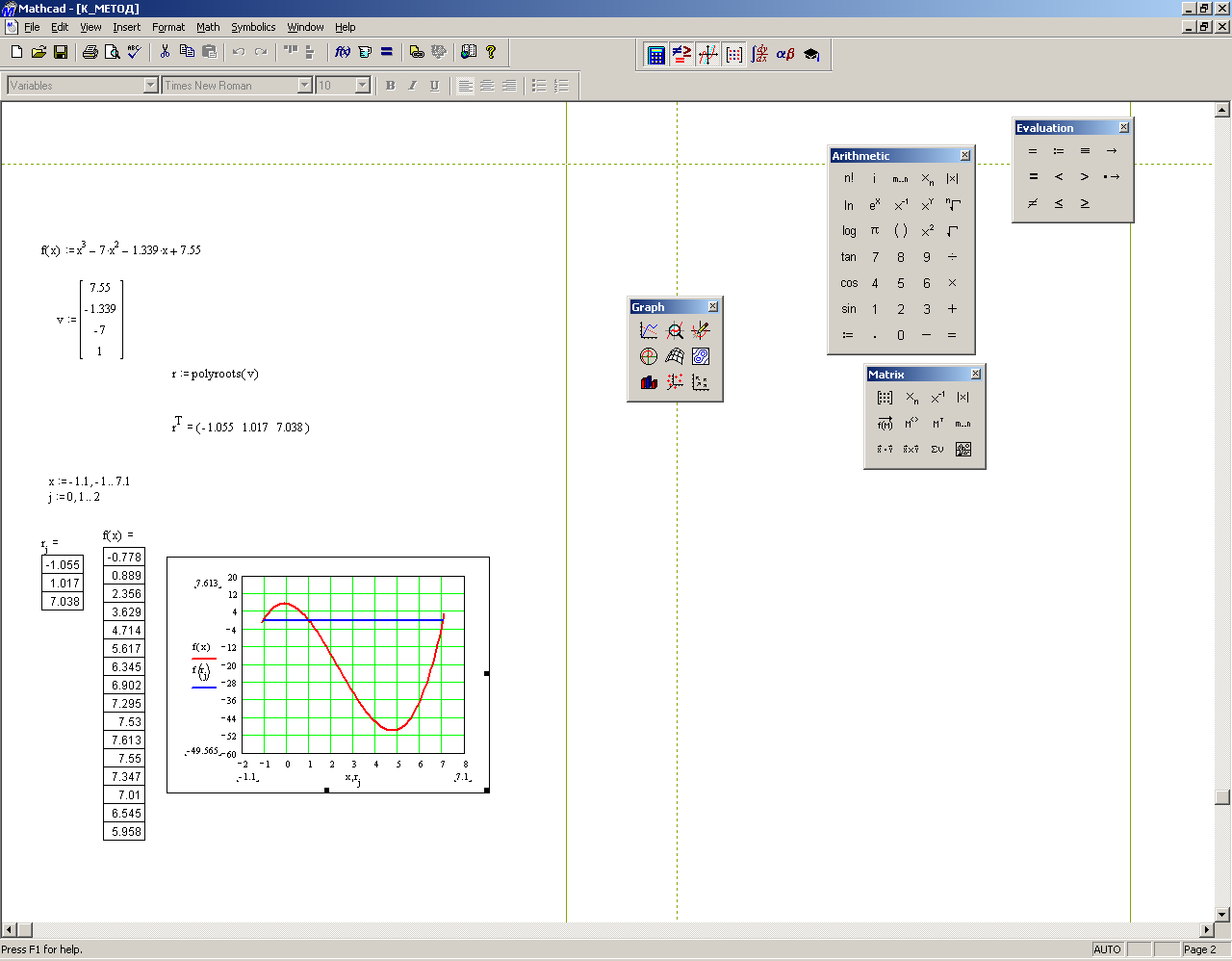 Рис.9.5 – Результат нахождения корней с использованием функции polyroots Задание 11. Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений. 1. Ввести левую часть уравнения. 2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =. 3. За знаком равенства ввести правую часть уравнения. 4. Выделить переменную, относительно которой решается уравнение. 5. Выбрать команду Symbolіc/Varіable/Solve. По окончанию решения корни уравнения выводятся в виде вектора. Пример. Для уравнения найти корни с использованием символьных решений уравнений.1. Записать левую часть уравнения  .2. Поставить логический знак «=» и в правой части записать 0. 3. Выделить переменную х. 4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve. Найдены корни уравнения запишутся в виде вектора: 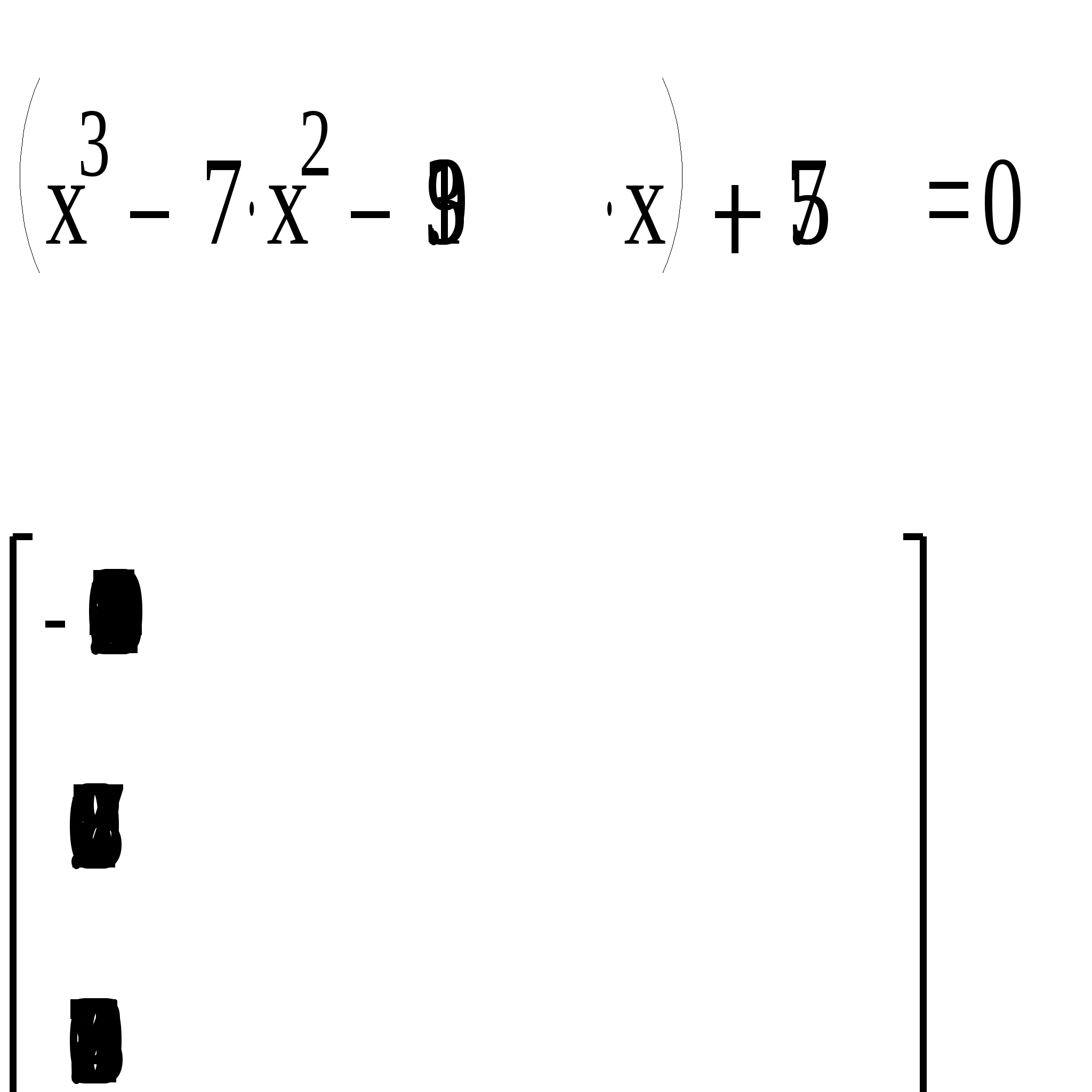 Задание 12. Найти приближенное решение с использованием функции mіnerr(x1,...). 1. Задать приближение последовательно для первого корня х:=1. 2. Ввести ключевое слово gіven (дано), из которого начинается блок решений. 3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения. 4. Обратиться к функции mіnerr( x). Корни будут найдены. Пример. Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…). 1. Задать приближение последовательно для первого корня х:=1. 2. Ввести ключевое слово given (дано), с которого начинается блок решений. 3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения. 4. Обратиться к функции minerr( x). Корень будет найден. 5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней. 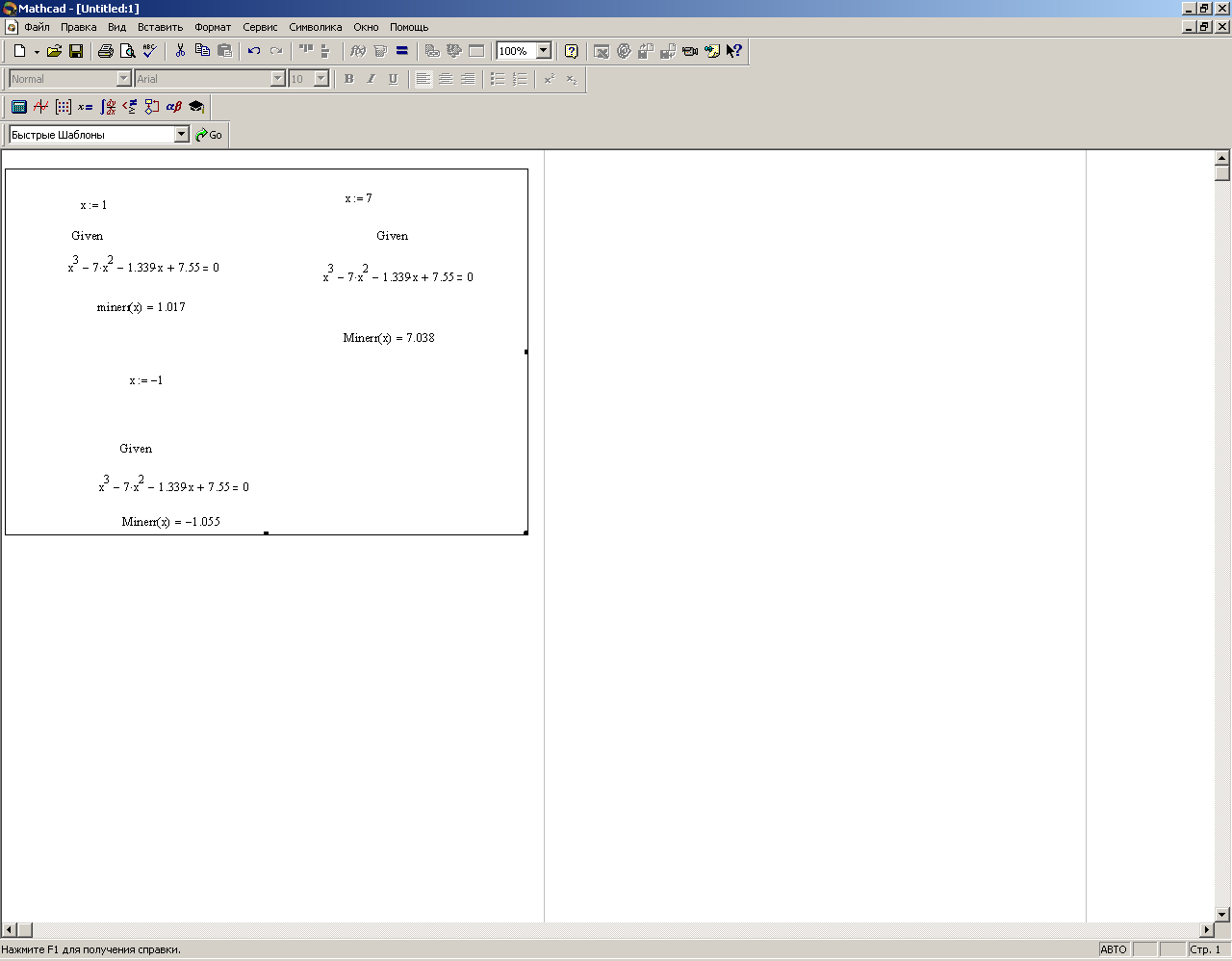 Таблица 7.1 – Варианты заданий к лабораторной работе
Задание 13. Действия с матрицами. 1. Создать матрицы 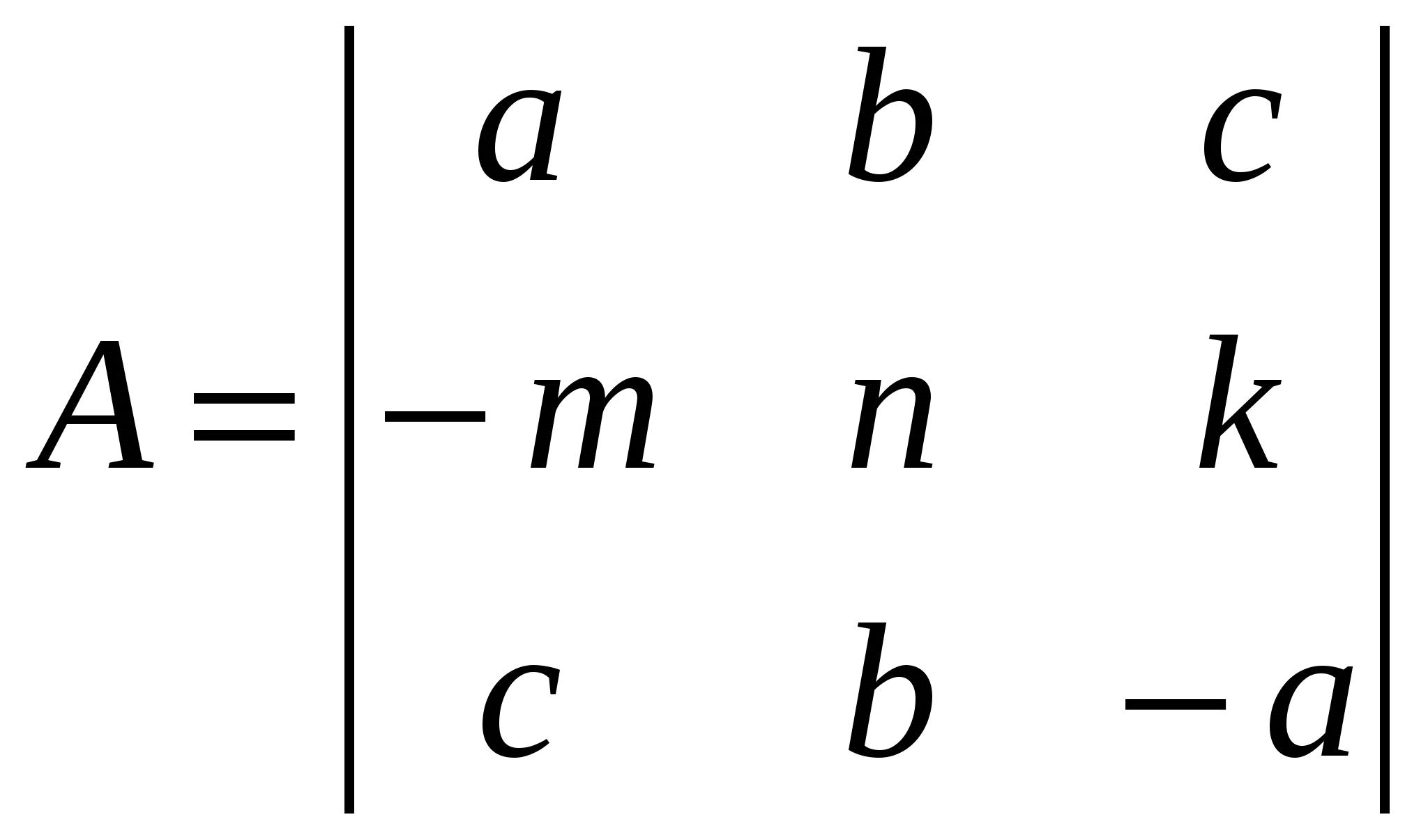 ,  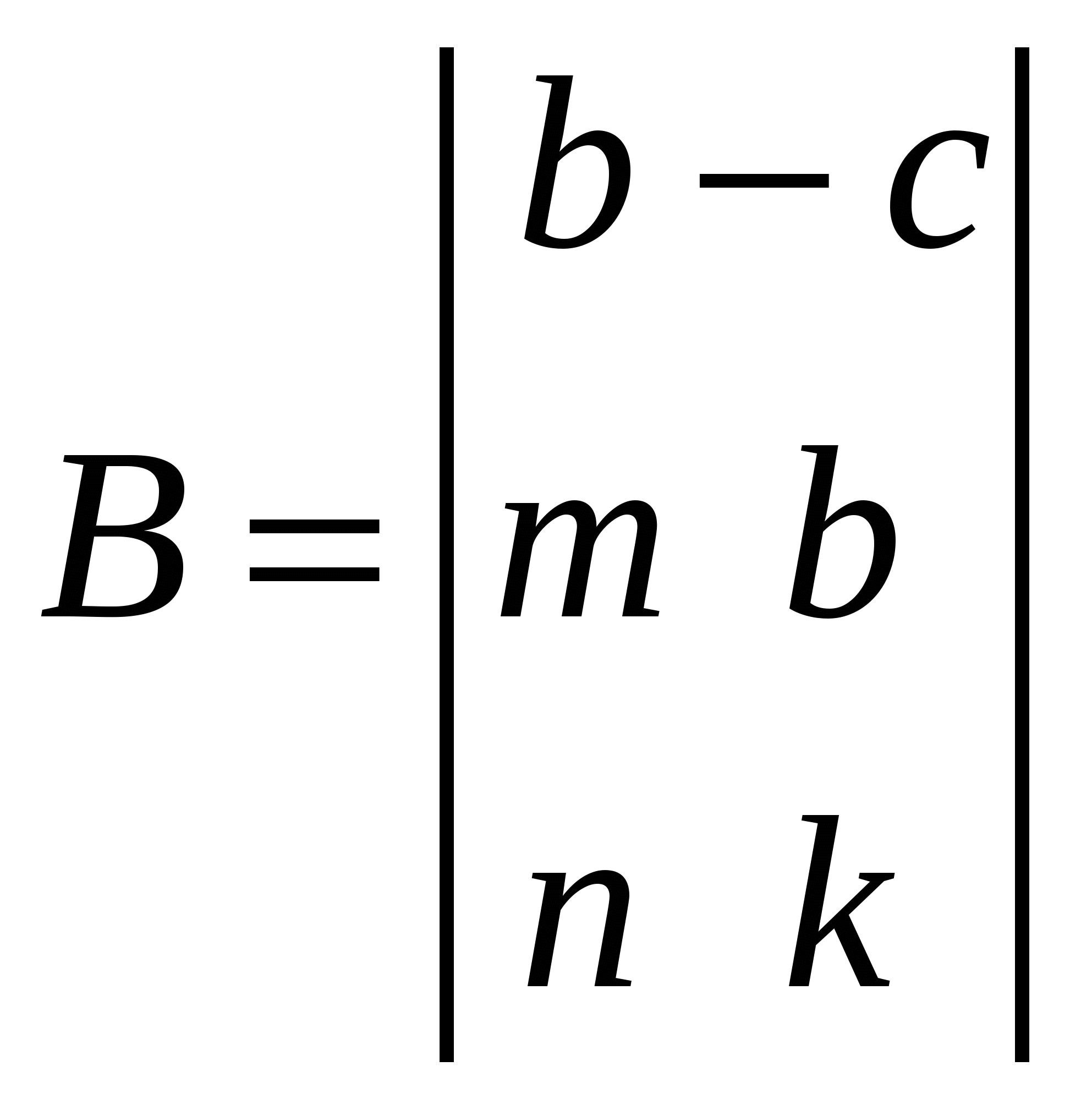,  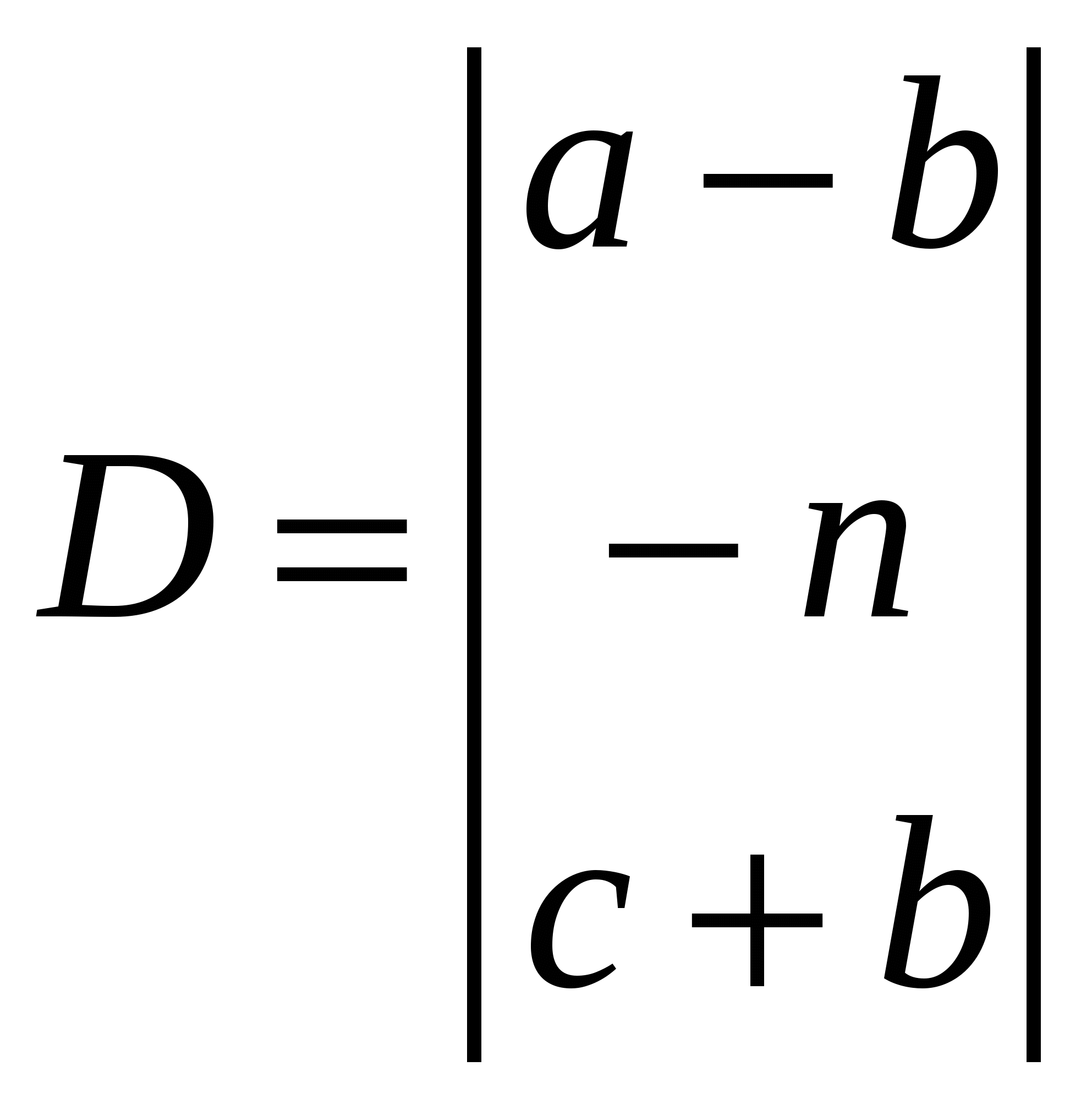,  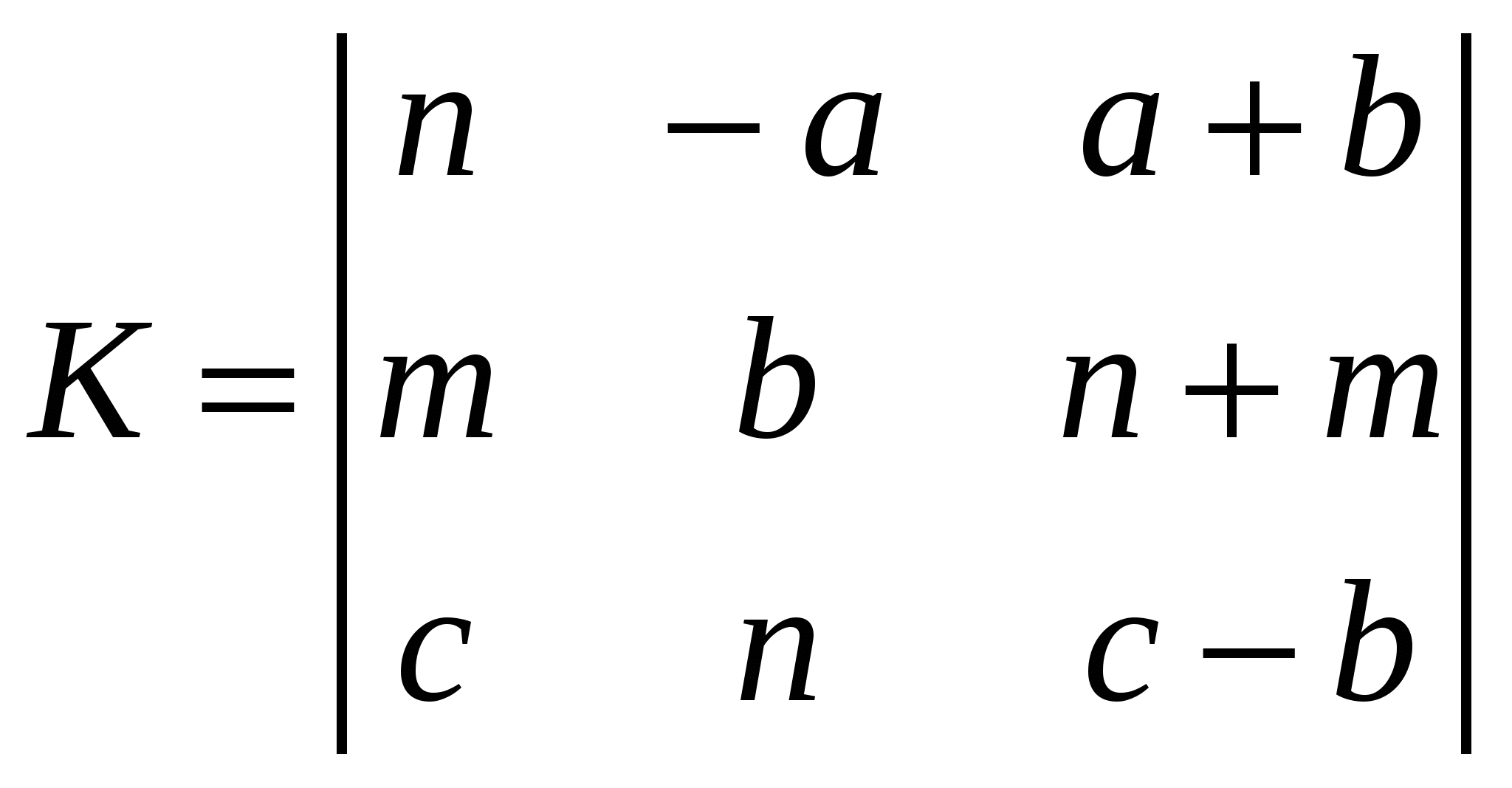,  ,  из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания (см. таблицу 7.2).2. Выполнить действия с матрицами в соответствии с вариантом задания. 3. Найти ранг матрицы А. 4. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А. 5. Найти обратную матрицу К. Найти детерминант матрицы А. Таблица 7.2. – Варианты к заданию 12
Пример. Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид: 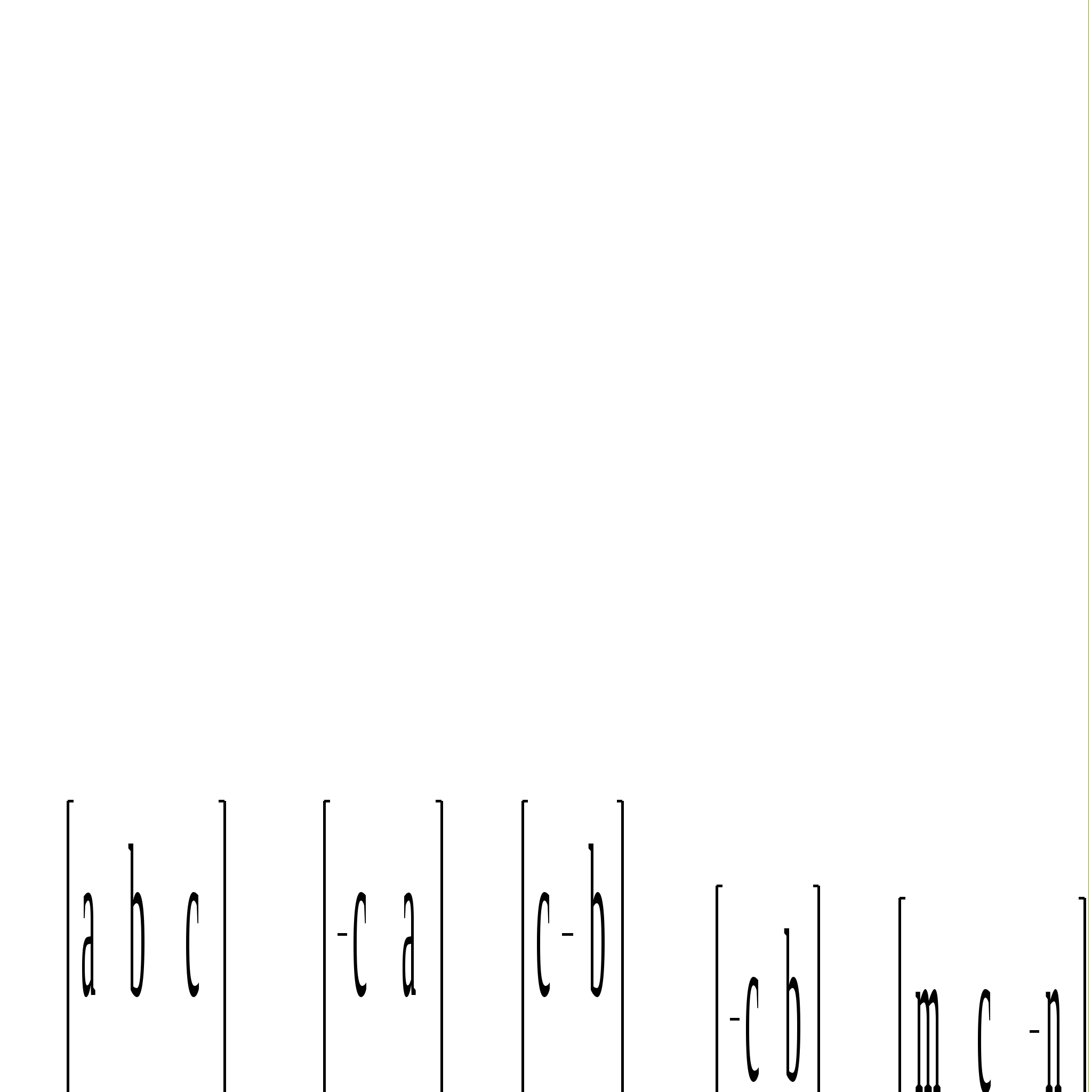  1. Создать матрицы. 1.1. Выбрать панель управления Matrіx (Матрица). 1.2. Определить число строк и столбцов для каждой матрицы (рис.7.6). 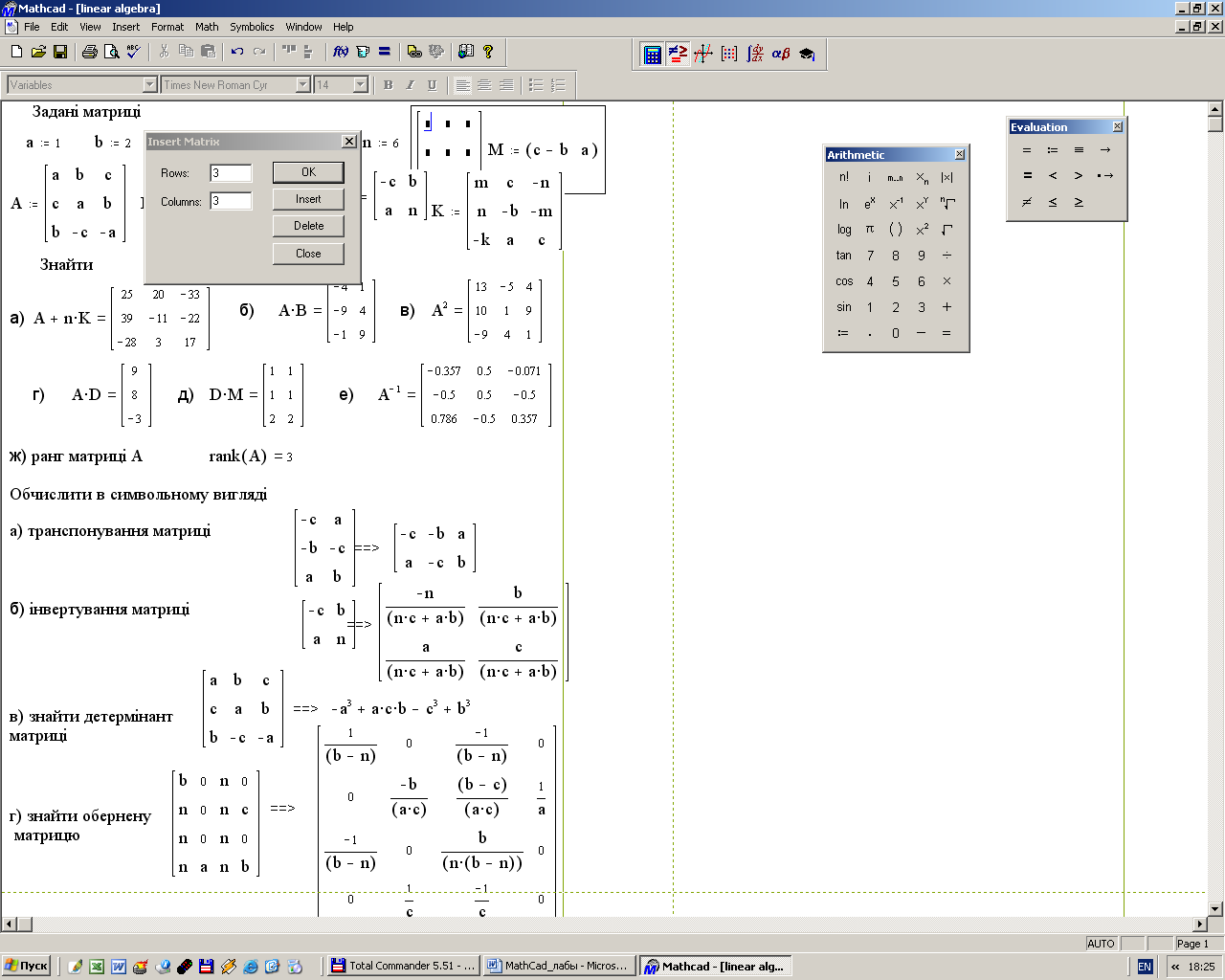 Рис.7.6 - Диалоговое окно для определения размера матрицы 1.3. Матрицы в примере имеют такие размеры: А - (33), В - (32), С(22), М(12), К(33). 1.4. Заполнить матрицы соответствующими параметрами. 2. Выполнить следующие действия с матрицами: 1) А+n·K; 2)A·B; 3) A2; 4) A·D; 5)D·M; 6) D-1. 3. Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A). 4. В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В. 4.1. Выделить матрицу В. 4.2. Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (Рис. 9.7). 5. В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) . 5.1. Выделить матрицу A. 5.2. Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.7.7). 6. В символьном виде найти обратную матрицу К. 6.1. Выделить матрицу К. 6.2. Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.7.7). 7. В символьном виде найти детерминант (определитель) матрицы А. 7.1. Выделить матрицу A. 7.2. Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.7.7). 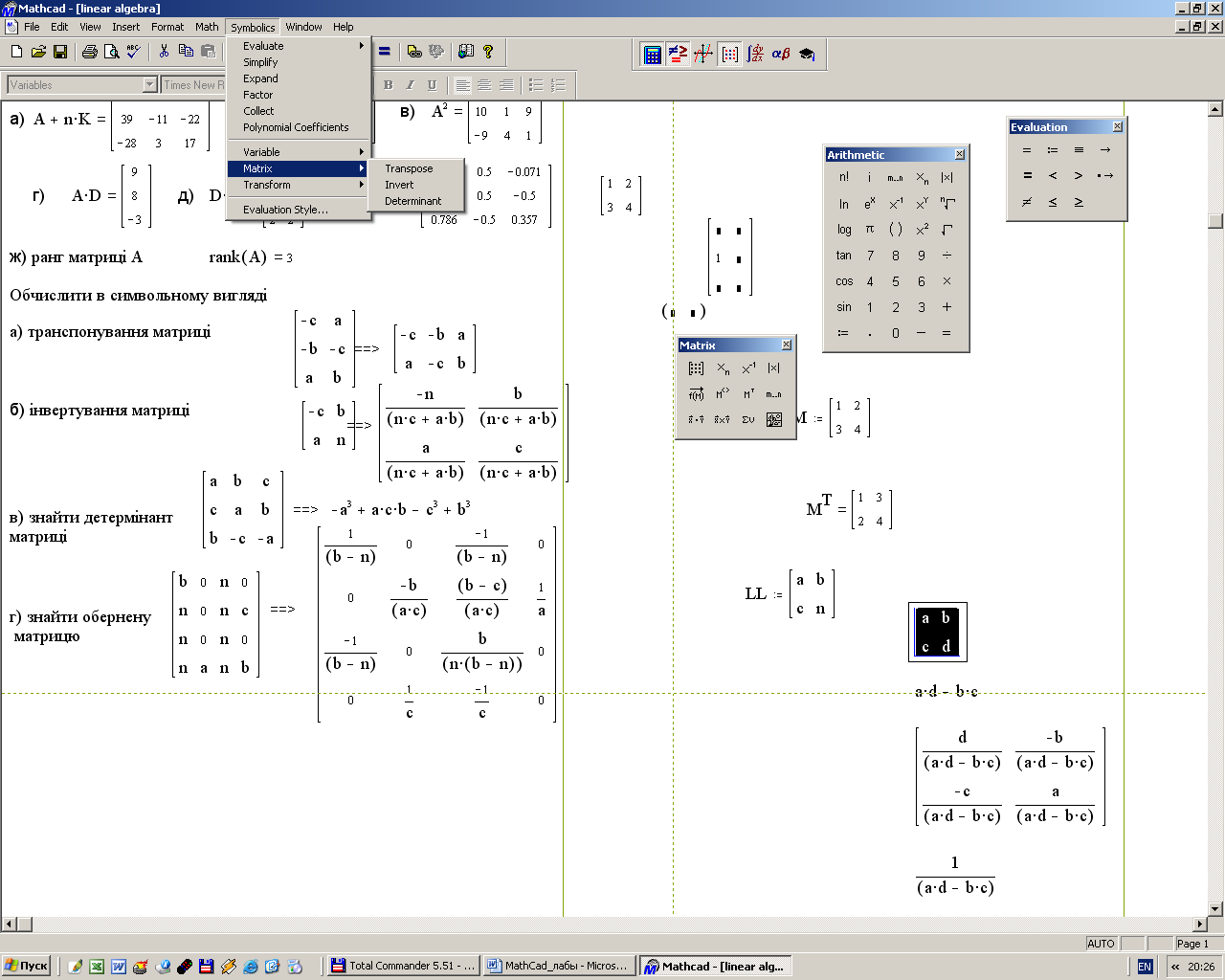 Рис. 9.7 – Меню Symbolic для работы с матрицами в символьном виде |