9. Расчет и конструирование слоистых д.к.. Проведенные экспериментальные исследования позволили установить
 Скачать 0.54 Mb.
|
|
Проведенные экспериментальные исследования позволили установить: 1. Наличие вертикальных колебаний аэродромной конструкции под действием ударных самолетных нагрузок. 2. Аэродромная конструкция, под действием ударной самолетной нагрузки, совершает от 5 до 9 колебаний, что не учитывается при ее проектировании. 3. Затухающие знакопеременные вертикальные колебания аэродромной конструкции ВПП при посадке ВС свидетельствуют о знакопеременном изгибающем моменте в слоях, существенно отличающегося от статического и приводящего к формированию знакопеременного затухающего напряженно-деформированного состояния аэродромной конструкции. 4. Аэродромные конструкции ВПП испытывают ударный импульс от 3,6 до 148 кН·с, частота вынужденных колебаний составляет 83-142 Hz. Её значение совпадает с выводами главы 6, а механика формирования волн в многослойной среде (6.4) качественно подтверждается приведенными экспериментами. 9. РАСЧЕТ И КОНСТРУИРОВАНИЕ СЛОИСТЫХ ДОРОЖНЫХ КОНСТРУКЦИЙ НА КРАТКОВРЕМЕННОЕ ВОЗДЕЙСТВИЕ ТРАНСПОРТНЫХ СРЕДСТВ Критериями динамической устойчивости слоистых конструкций при воздействии на них подвижных нагрузок могут выступать: а – динамический прогиб поверхности – uдин; б – скорость вертикальных колебаний – úдин; в – ускорения вертикальных колебаний – üдин; г – частота вынужденных колебаний; Наличие нескольких критериев устойчивости объясняется их различной чувствительностью на изменение условий нагружения конструкции подвижной нагрузкой. Так, например, динамический упругий прогиб малозаметно изменяется в зависимости от скорости движения нагрузки, в то время как скорости и ускорения колебаний существенно зависят от неё. Кроме того скорости колебаний и ускорения лучше измеряются современными средствами измерений, но являются производными от прогиба. В целом же критерии динамической устойчивости слоистых дорожных конструкций чрезвычайно вариабельны. Так при движении со скоростью V по поверхности одной и той же конструкции прогибы, их формы, скорости вертикальных колебаний и ускорений зависят от конструкции транспортных средств (автомобилей и самолетов), числа осей и колес. Деформационное состояние конструкции при этом различно при проезде разных транспортных средств и смена его вертикальной направленности наблюдается от 4 до 9 раз, а частота этой смены при скорости в 100 км/ч для автотранспорта составляет 14-85 Hz. и для воздушных судов при посадочной скорости в 300 км/ч 170-240 Hz. Представляемый ниже метод расчета толщины слоев дорожных конструкций предполагает их динамическую устойчивость под действием подвижной нагрузки в случае выполнения условия – динамический прогиб поверхности покрытия многослойной дорожной конструкцией от действия подвижной расчетной нагрузки не должен превышать допустимый; сопротивление грунта Uдин< [U] (9.1) здесь U – динамический прогиб поверхности конструкции от действия подвижной расчетной нагрузки; [U] – допустимый прогиб поверхности конструкции, гарантирующий её сплошность. Технология расчета дорожных конструкций, пригодных в основном для участков дорог и автомагистралей с высокой скоростью движения сводится к предварительному назначению числа и толщины слоев покрытий, оснований и подстилающих слоев с заданными характеристиками прочности и деформативности и перебору вариантов их соотношений до выполнения условий 9.1. Для каждого варианта составляется расчетная схема, аналогичная рис. 9.1, а, а дорожная конструкция может быть создана по принципу ступенчатого изменения плотности слоев по ее толщине (рис. 9.1, в) или убывающего (рис. 9.1, б). В первом случае на границах с более плотными слоями возникает эффект отражения волн напряжений. Нагрузка на поверхность конструкции q(t) действует кратковременно в течение 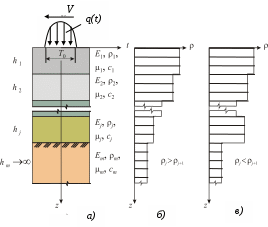 (здесь D – длина продольного контакта колеса с покрытием и равная диаметру кругового следа) и задана функцией  . Слоистая среда, нижний слой которой – упругое полупространство неограниченной толщины hм → ∞, характеризуется числом слоев М, а любой j-й слой (1 < j < М) – толщиной hj модулем упругости Еj, коэффициентом Пуассона vj, плотностью ρj и скоростью распространения продольной волны cj. Отдельный слой толщиной hj, загружаемый сверху напряжением σj-1 начинает воспринимать действие напряжений со времени: . (9.2) Рис. 9.1. Расчетная схема слоистой дорожной конструкции (а) и принципы конструирования её при ступенчато убывающей (б) и ступенчато возрастающей плотности слоев (в) Процесс преодоления напряжениями сжатия от кратковременных колесных поверхностных давлений q слоистой конструкции состоит в последовательном от слоя к слою пробеге зоной сжатия каждого слоя со скоростью распространения продольных волн сj. Поэтому время действия напряжений в слоях конструкции увеличивается с ростом числа и толщины слоев, а значение напряжений убывает. В табл. 9.1. приведен блок формул для вычисления этого времени и времени максимальных напряжений. Таблица 9.1 Время действия и образования максимума напряжений сжатия в слоях конструкций
В табл.9.1  ;  ; g = 980 см/с2.Максимальное напряжение сжатия в слое составит:  (9.3)где а = 1÷2,5, (а = 1 для упруговязкопластичных конструкций с асфальтобетонными покрытиями); (а = 1 для упруговязких конструкций с цемнтобетонными покрытиями);  ; q– принимают как удельное давление под колесом.Упругий динамический прогиб слоя составит:  (9.4)а всей слоистой конструкции:  (9.5)Если слоистая конструкция создана по принципу ступенчатого изменения плотности слоев по толщине, то на границе слоев при ρj < ρj+1 возникают отраженные напряжения: 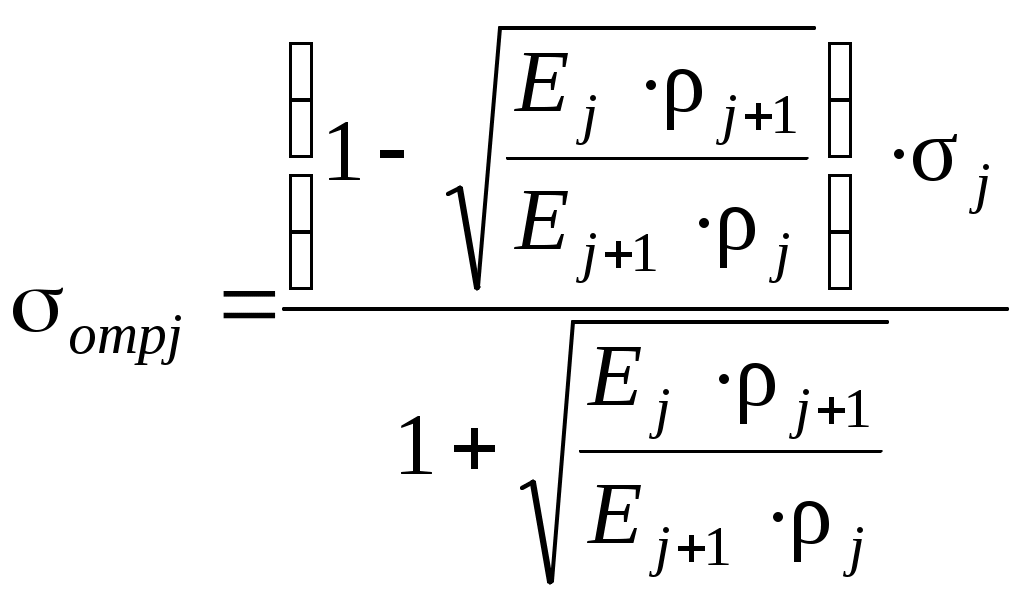 . (9.6)В этом случае динамический прогиб конструкции составит:  (9.7)Значение допустимого динамического прогиба для автомобильных нагрузок принимают из табл. 8.1.1. Расчетные механические свойства материалов для расчета конструкций дорог и аэродромов принимают по Приложениям к нормативным методам, а прогибы по табл. 9.2. Таблица 9.2 Допускаемый динамический прогиб конструкций взлетно-посадочных полос и аэродромов
Расчет динамического напряженно-деформированного состояния (ДНДС) слоистой конструкции сводится к выполнению вышеприведенного алгоритма, условия 9.1 с точностью +5 % и представлении ДНДС примененным во времени. При этом вычисляются и производные от ДНДС и в частности: скорость вертикальных колебаний (úдин) и ускорения (üдин). Представленные последовательно формулы начиная с 9.2, таблицы 9.1 есть алгоритм расчетной программы DINWAY-2 на реализации которой построены последующие выводы. В качестве примера из программы DINWAY-2 покажем её работу по расчету ДНДС дорожной и аэродромной конструкции из цементобетонного покрытия из бетона класса В40 толщиной 28 см, цементогрунтового основания из супеси, укрепленной цементом 1 марки прочности и толщиной 20 см и грунтового основания из суглинка при относительной влажности 0,7. Расчеты вертикальных прогибов, скоростей и ускорений колебаний этой конструкции в относительном времени (t/T0) и их изменений по траектории движения (S, м) приведены для воздействия на неё нагрузки группы А1 с нагрузкой на ось 100 кН и при скорости её движения V = 60 км/ч и для воздействия самолетной нагрузки от самолета БОИНГ 747-400 с нагрузкой на 4-х колесную опору 463,6 кН и при посадочной скорости V = 260 км/ч. Результаты представлены на рис. 9.2 и 9.3. Из них следует, что одна и та же конструкция устроенная на автомагистрали и взлетно-посадочной полосе аэродрома испытывает на последней более сложное и тяжелое динамическое деформационное состояние (ДДС) проявляющееся в том, что при увеличении на неё подвижной колесной нагрузки лишь в 4,63 раза, динамический прогиб (вертикальные колебания) увеличивается в 22 раза, скорость колебаний в 120 раз, а ускорение в 80 раз. Кроме этого из рис. 9.2, 9.3 и 9.4 следует, что принятая для расчета конструкция: - пригодна для дороги только III категории, т.к. динамический прогиб в 0,38 мм меньше допустимого в 0,406 мм (см. табл. 9.1); - непригодна для устройства ВПП аэродрома, т.к. динамический прогиб в 6,5 мм от самолета БОИНГ 747-400 больше допустимого в 1,66 м (см. табл. 9.2) и поэтому требуется увеличение толщины конструкции; - допускает проникание заметных динамических напряжений сжатия от автомобильной нагрузки А1 (100 кН на ось) на глубину 129 см, а от самолетной (БОИНГ 747-400) на глубину 171 см. В месте с этих высокочастотных колебаний локализованы в основном в покрытии и основании конструкции; - форма вертикальных перемещений конструкции, её затухающий во времени характер совершенно не адекватна статической теории изгиба плит и многослойных сред. 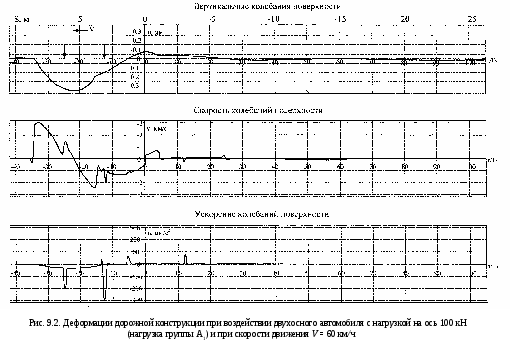 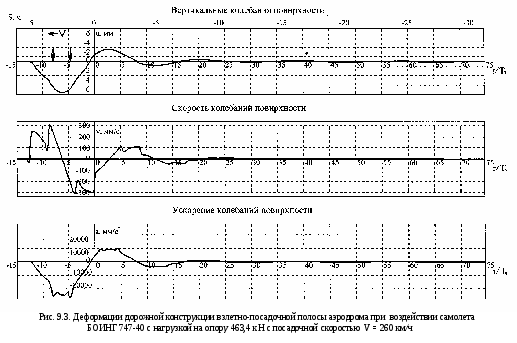 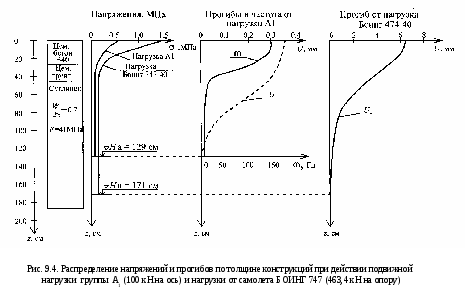 9.1. Комбинаторный метод расчета толщины дорожных | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
