|
|
лекция. Прямая на плоскости
Лекция 4
Глава 3
Прямая на плоскости
3.1. Понятие уравнения линии
Предположим, что на плоскости  задана декартова прямоугольная система координат задана декартова прямоугольная система координат 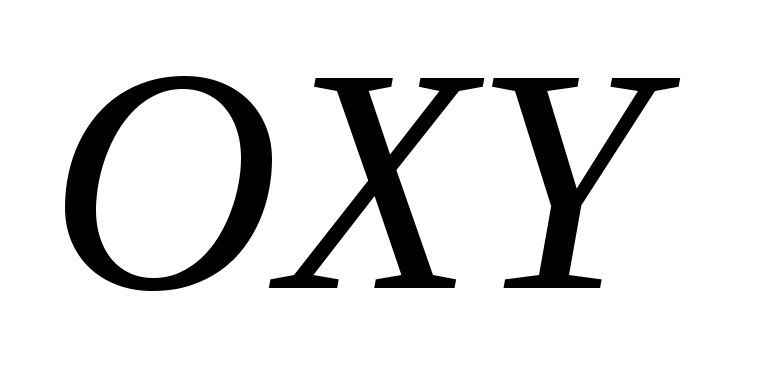 и некоторая линия и некоторая линия  . .
Рассмотрим уравнение
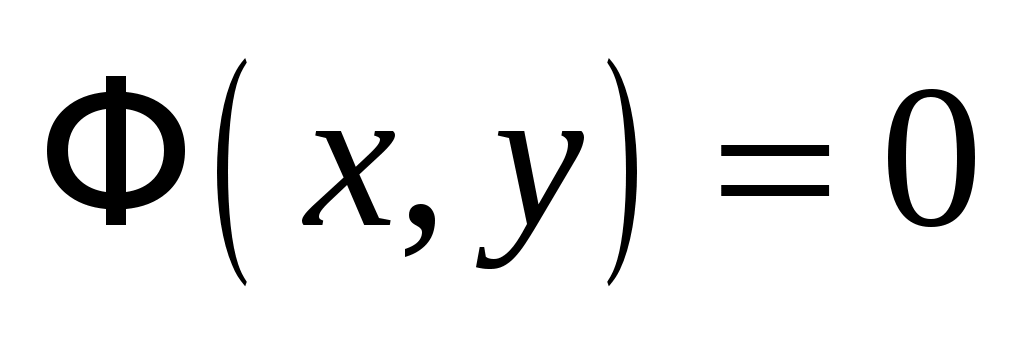 , (3.1) , (3.1)
связывающее две переменные  и и 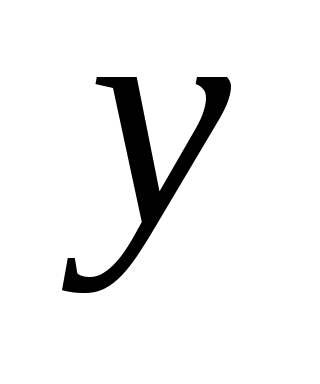 . .
Определение 1. Уравнение (3.1) называется уравнением линии  относительно заданной системы координат, если уравнению (3.1) удовлетворяют координаты относительно заданной системы координат, если уравнению (3.1) удовлетворяют координаты  и и 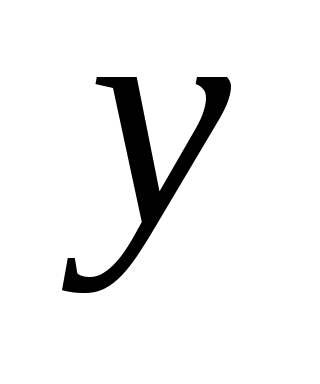 любой точки, лежащей на линии любой точки, лежащей на линии  , и не удовлетворяют координаты , и не удовлетворяют координаты  и и 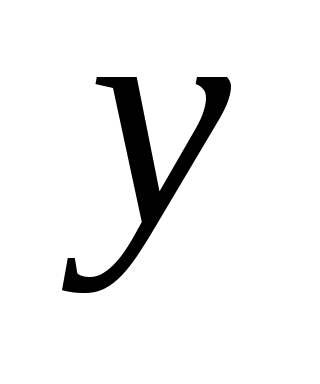 ни одной точки, не лежащей на линии ни одной точки, не лежащей на линии  . .
Согласно этому определению сама линия  представляет собой геометрическое место точек, координаты которых удовлетворяют уравнению (3.1) представляет собой геометрическое место точек, координаты которых удовлетворяют уравнению (3.1)
Если в заданной системе координат уравнение (3.1) является уравнением линии  , будем говорить, что (3.1) определяет линию , будем говорить, что (3.1) определяет линию  . .
Пример 1. Пусть фиксирована декартова система координат 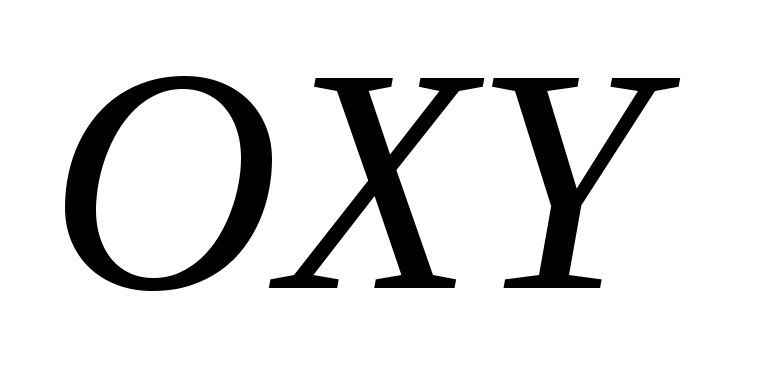 . Требуется показать, что уравнение . Требуется показать, что уравнение
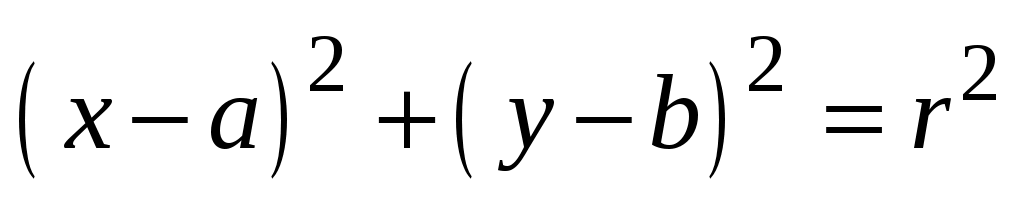 (3.2) (3.2)
является уравнением окружности радиуса 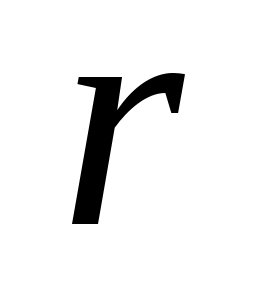 с центром в точке с центром в точке  . .
Окружность по определению есть геометрическое место точек (совокупность тех и только тех точек), для каждой из которых расстояние до некоторой фиксированной точки есть величина постоянная.
Пусть  – окружность радиуса – окружность радиуса 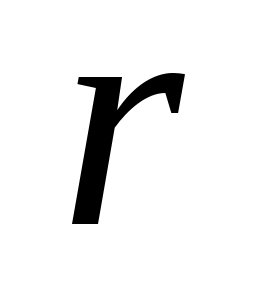 с центром в точке с центром в точке  . .
  (рис. 3.1), или (рис. 3.1), или 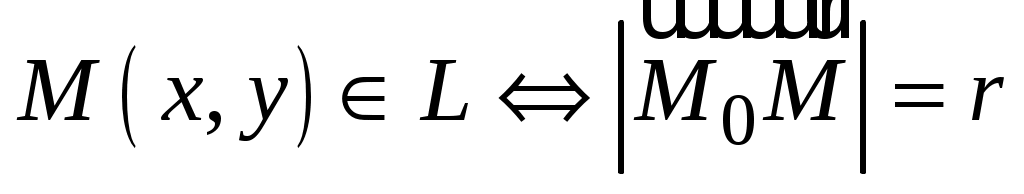 , или , или 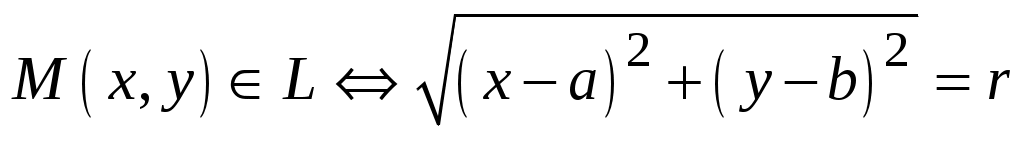 , или , или
 – –
уравнение (3.2) в соответствии с определением 1 действительно определяет окружность  . .
Определение 2. Линия  называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением (3.1), в котором называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением (3.1), в котором 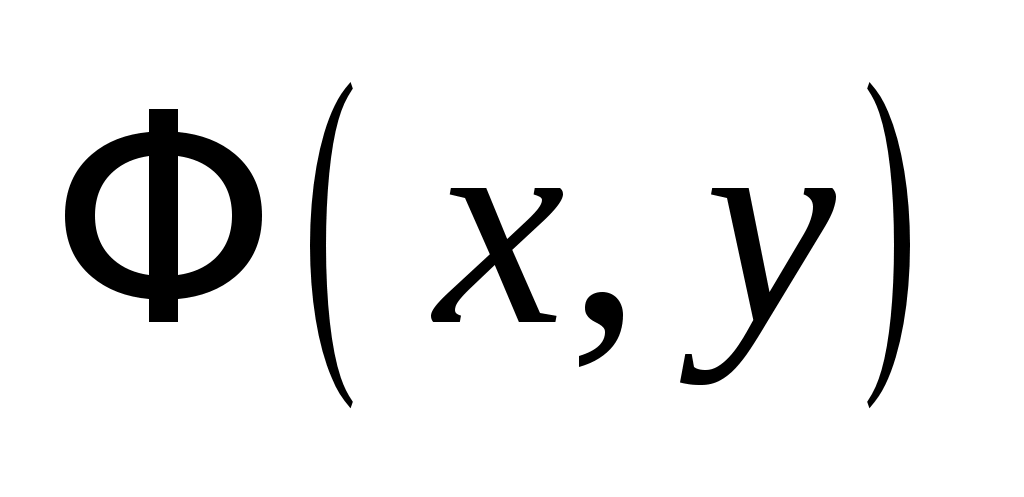 – алгебраический полином (т.е. сумма конечного числа слагаемых вида – алгебраический полином (т.е. сумма конечного числа слагаемых вида 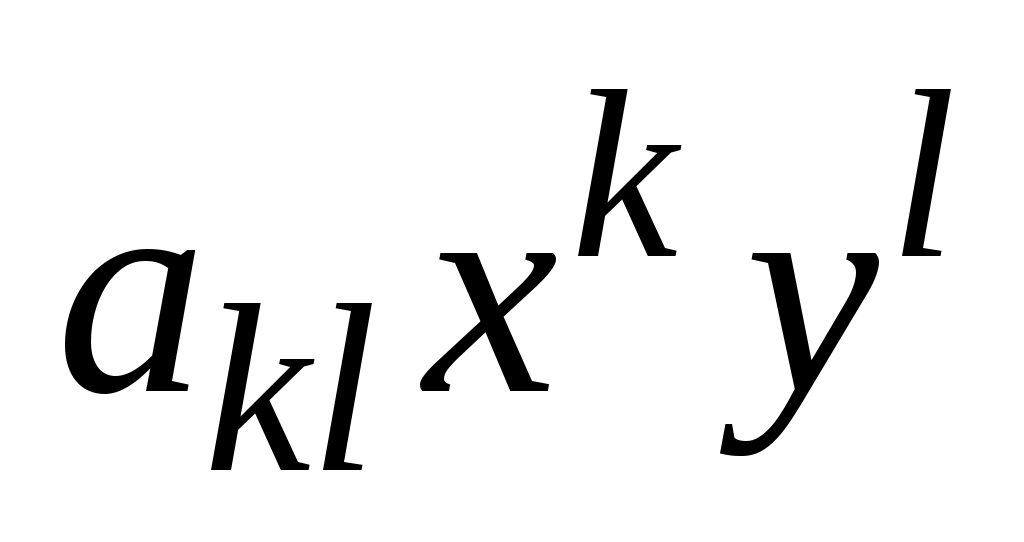 , ,  – целые, – целые,  – некоторая постоянная). – некоторая постоянная).
Если при этом 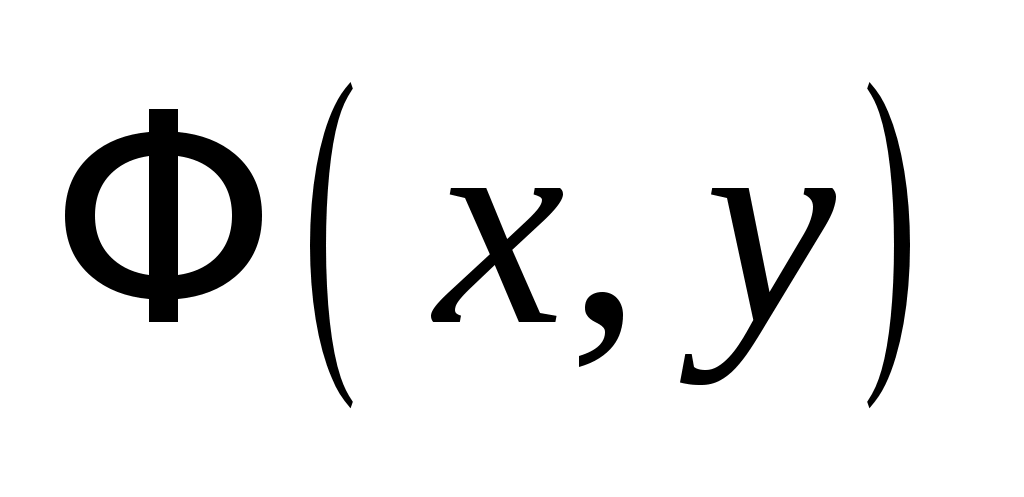 – алгебраический полином порядка – алгебраический полином порядка  , линия , линия  называется линией порядка называется линией порядка  . .
Например, окружность – алгебраическая линия второго порядка (см. пример 1).
Определение 3. Всякая неалгебраическая линия называется трансцендентной.
Приведем без доказательства следующее утверждение.
Теорема 1. Если линия  в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени  , эта линия и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени , эта линия и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени  . .
3.2. Уравнение прямой в общем виде
Теорема 2. Пусть фиксирована декартова система координат 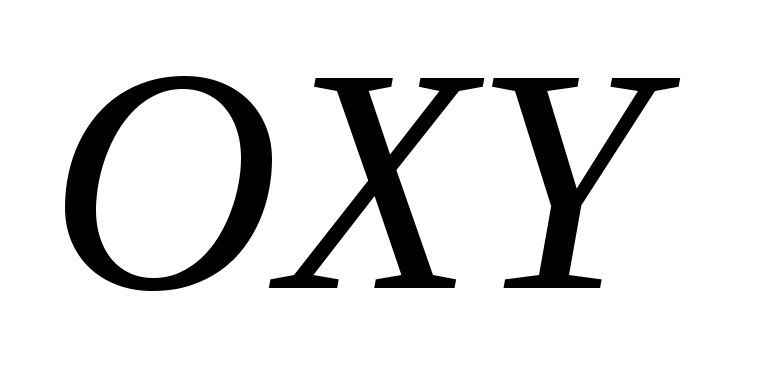 . Всякое уравнение вида . Всякое уравнение вида
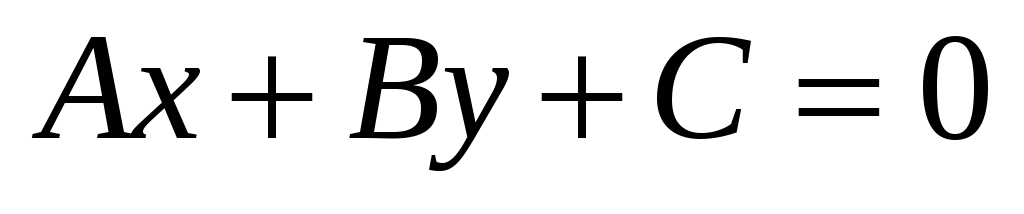 , (3.3) , (3.3)
где 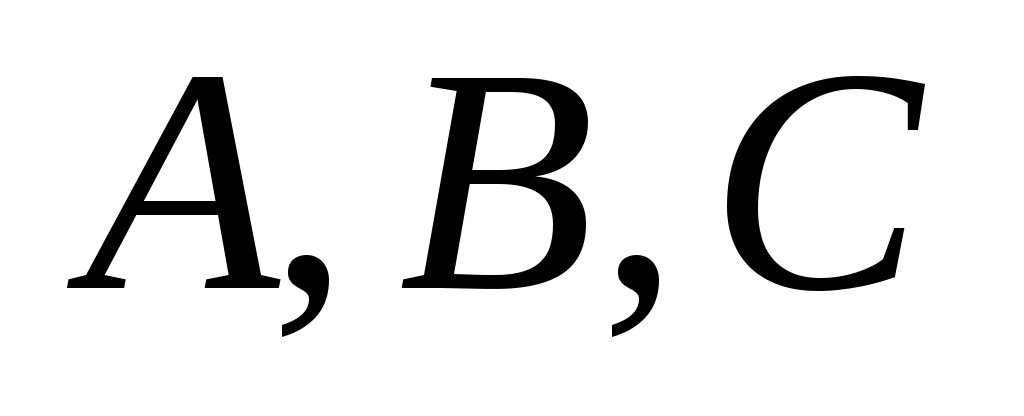 – действительные числа, причем – действительные числа, причем  и и 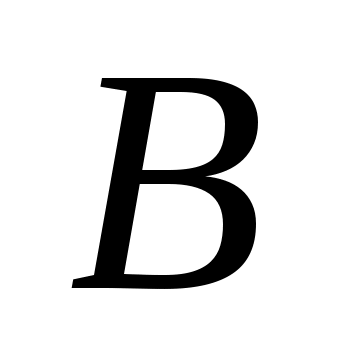 не равны нулю одновременно, определяет на плоскости прямую линию. не равны нулю одновременно, определяет на плоскости прямую линию.
Доказательство. Пусть 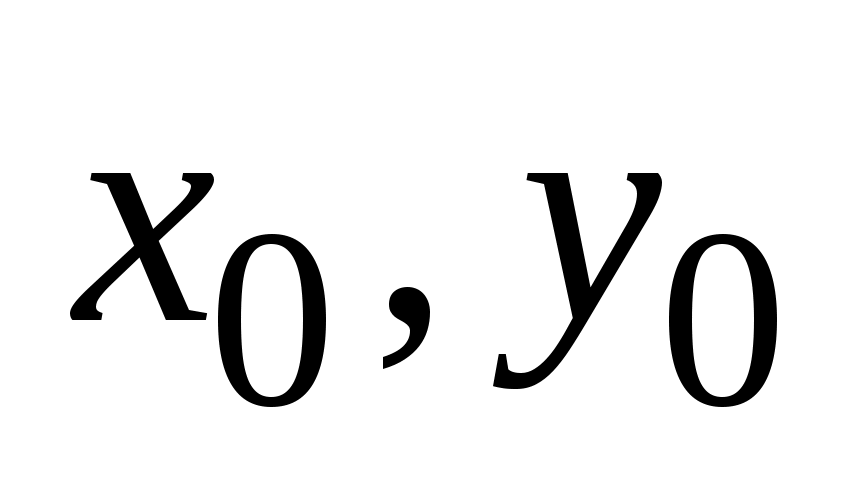 – решение (3.3). – решение (3.3).
Уравнение (3.3) имеет хотя бы одно решение ( и и 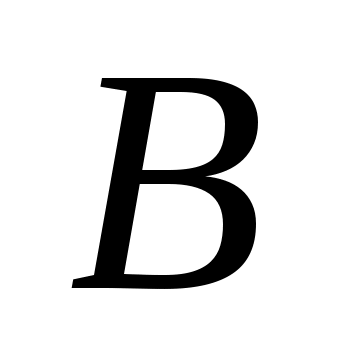 не равны нулю одновременно, пусть для определенности не равны нулю одновременно, пусть для определенности 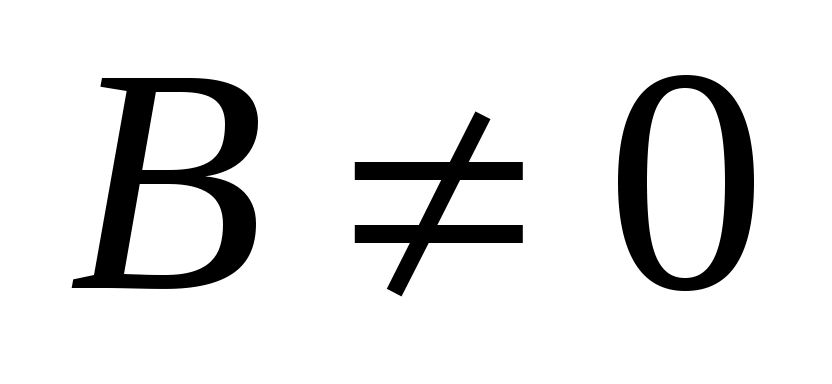 , тогда , тогда  , полагаем , полагаем 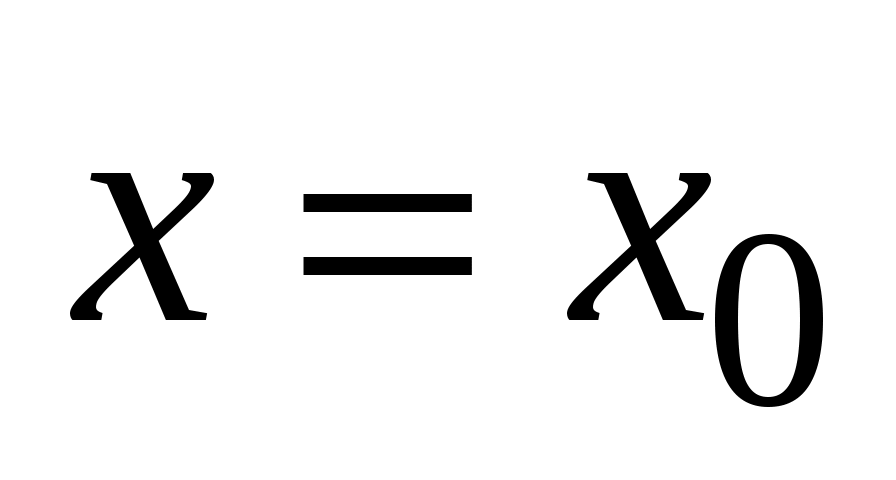 и получаем и получаем  , и пара , и пара  – решение (3.3)). – решение (3.3)).
Тогда справедливо тождество
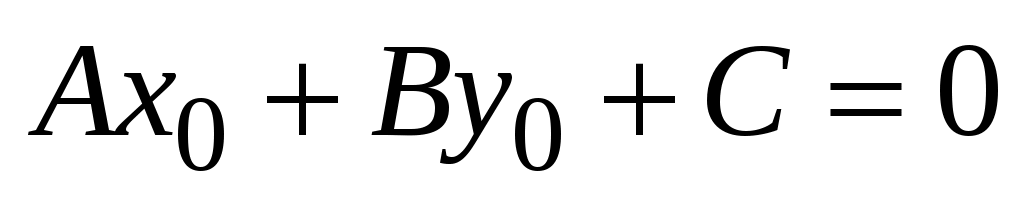 . (3.4) . (3.4)
Пусть 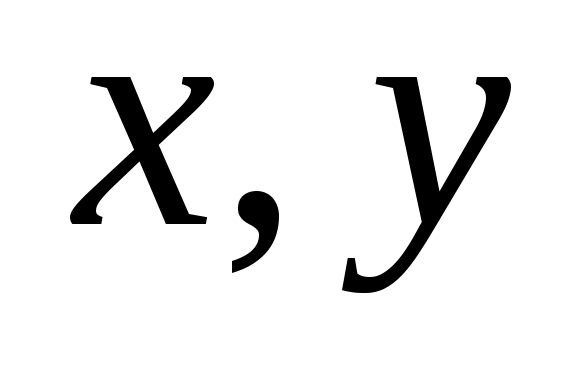 – другое решение (3.3). Тогда выполняется тождество – другое решение (3.3). Тогда выполняется тождество
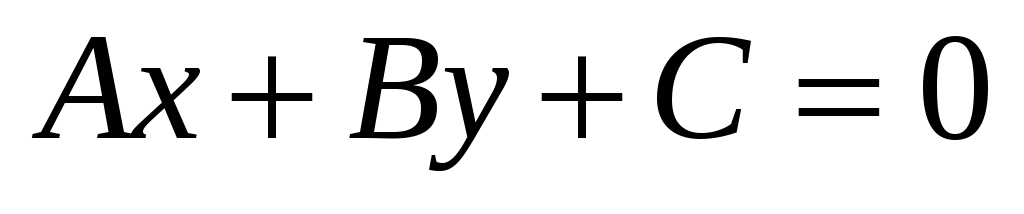 . (3.5) . (3.5)
Вычтем из (3.5) почленно (3.4):
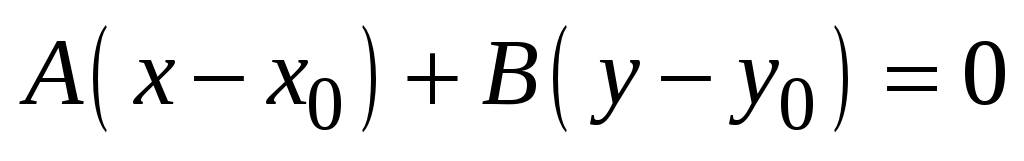 . (3.6) . (3.6)
Пусть  – точка с координатами – точка с координатами  , а , а  – точка с координатами – точка с координатами 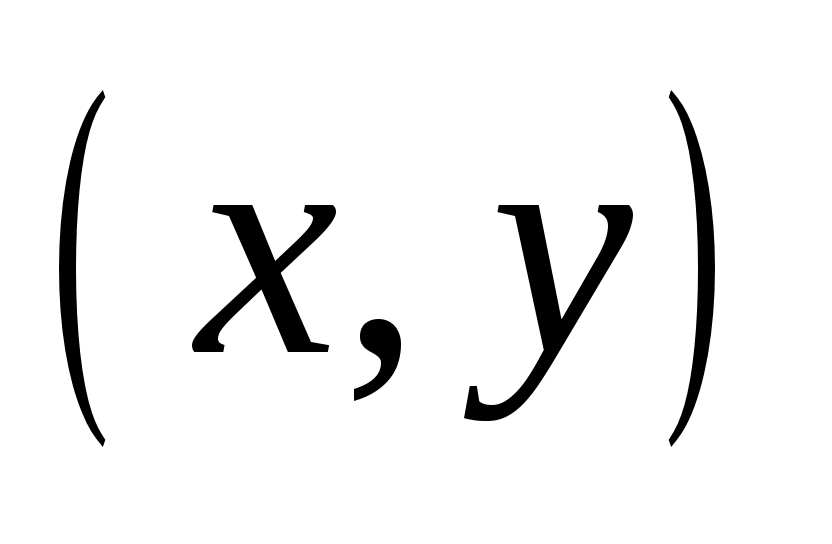 . Тогда . Тогда 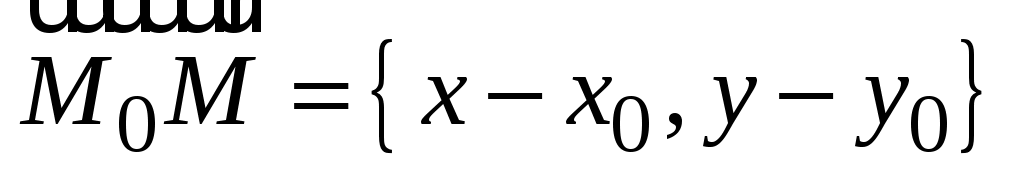 . .
Введем в рассмотрение вектор 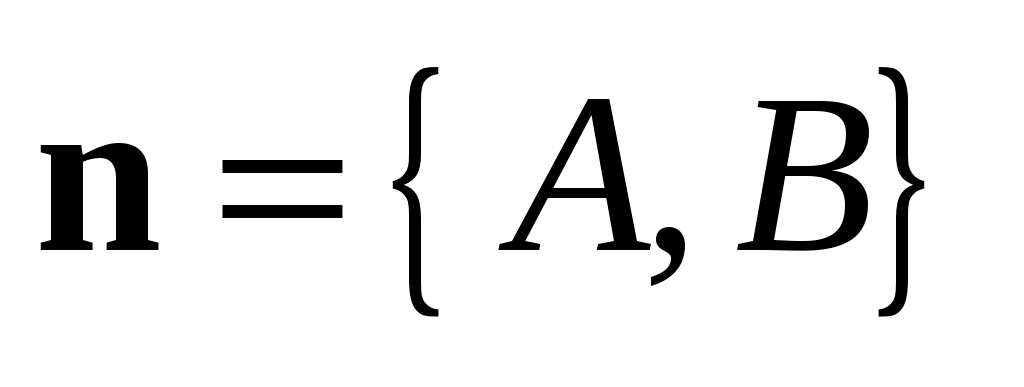 . Равенство (3.6) выполняется тогда и только тогда, когда . Равенство (3.6) выполняется тогда и только тогда, когда 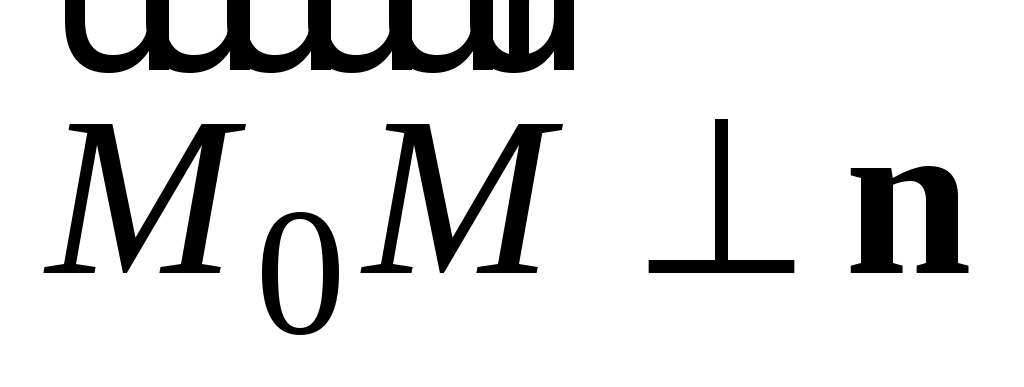 . .
(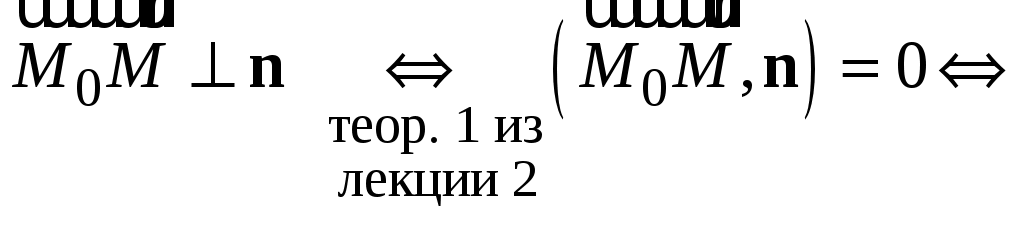
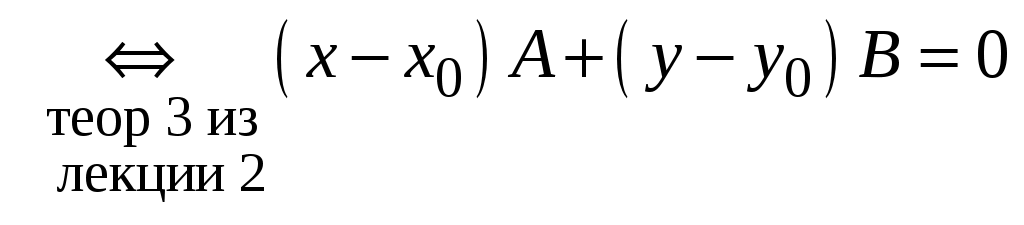 ). ).
Т аким образом, если пара чисел аким образом, если пара чисел 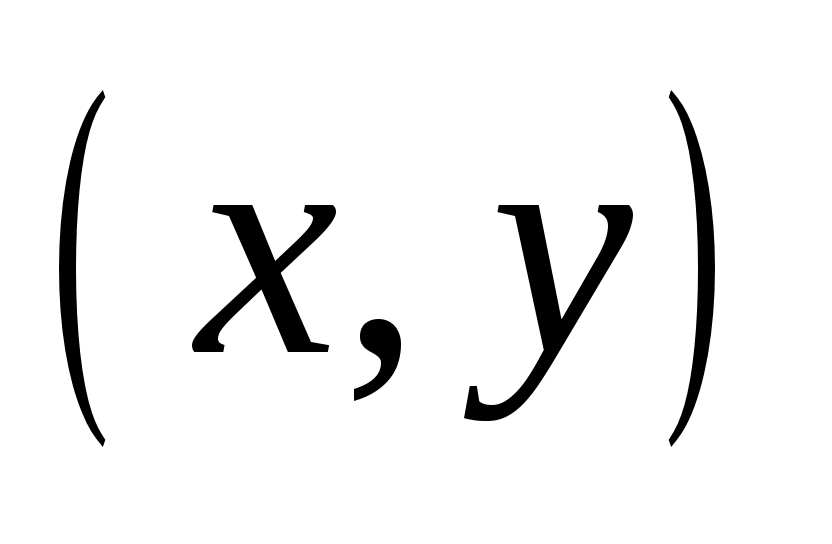 удовлетворяет (3.3), то точка удовлетворяет (3.3), то точка 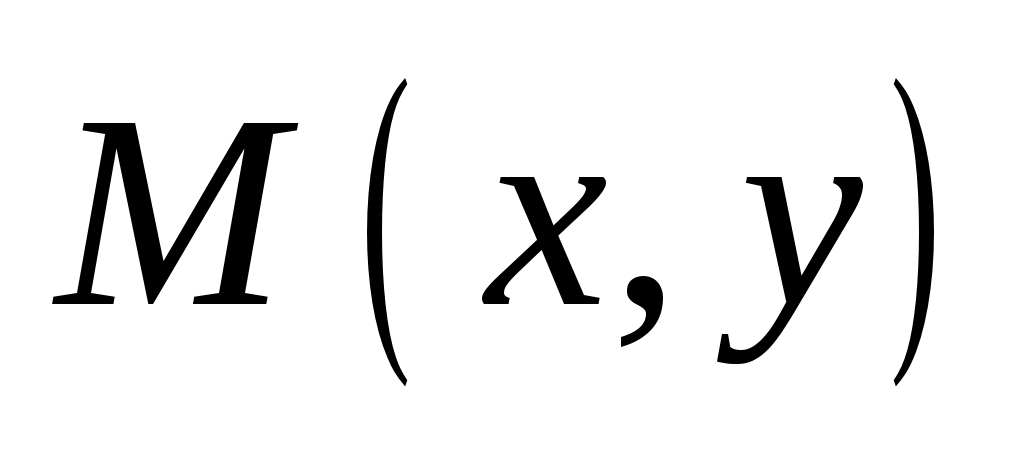 является концом вектора является концом вектора 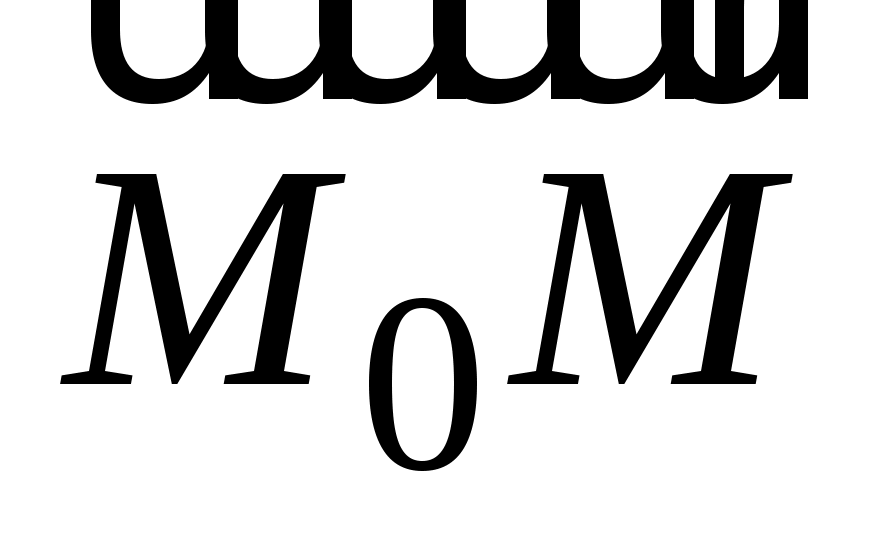 , перпендикулярного , перпендикулярного  и, следовательно, принадлежит прямой и, следовательно, принадлежит прямой  , проходящей через точку , проходящей через точку  и перпендикулярной и перпендикулярной  (рис. 3.2). (рис. 3.2).
Обратно. Пусть  принадлежит прямой принадлежит прямой  , проходящей через точку , проходящей через точку  и перпендикулярной и перпендикулярной 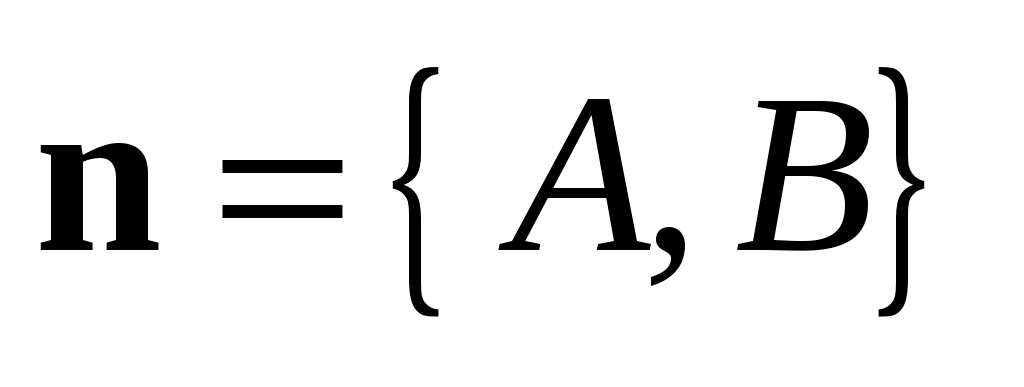 . Тогда . Тогда 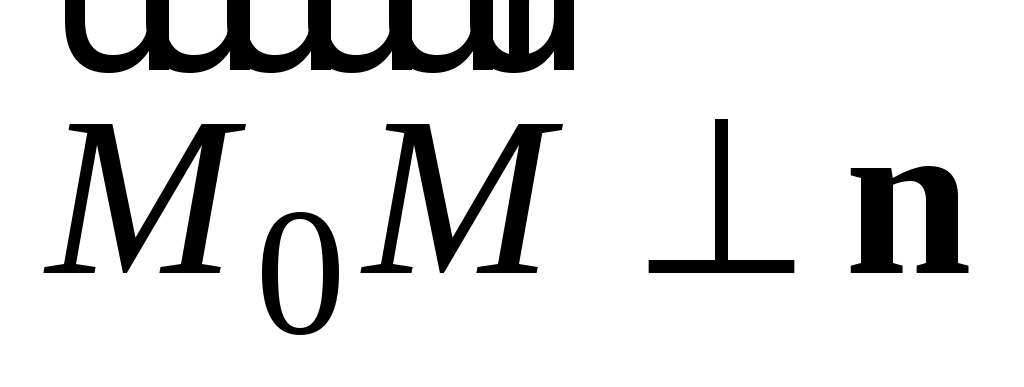 и выполняется равенство (3.6), а значит, с учетом (3.4) выполняется (3.5) или, что то же самое, уравнение (3.3), и пара чисел и выполняется равенство (3.6), а значит, с учетом (3.4) выполняется (3.5) или, что то же самое, уравнение (3.3), и пара чисел  и и 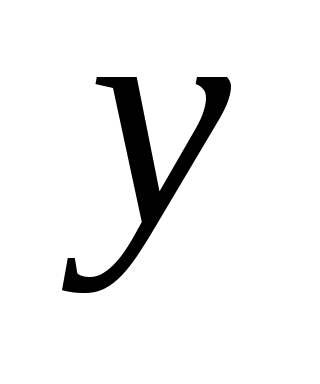 является решением (3.3), следовательно, (3.3) – уравнение прямой является решением (3.3), следовательно, (3.3) – уравнение прямой  . .
Уравнение (3.3) называется общим уравнением прямой, вектор 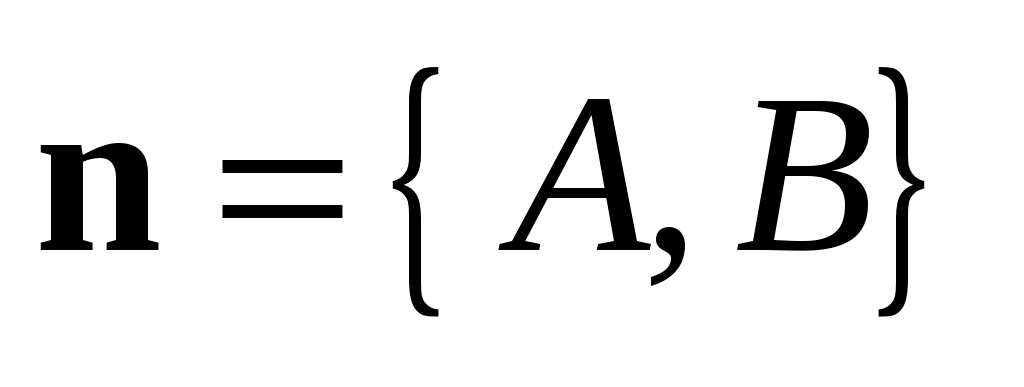 – нормальным вектором прямой. – нормальным вектором прямой.
Если хотя бы один из коэффициентов в уравнении (3.3) равен нулю, уравнение называется неполным.
Упражнение. Выяснить особенности расположения относительно осей координат прямой, задаваемой неполным уравнением:
1) 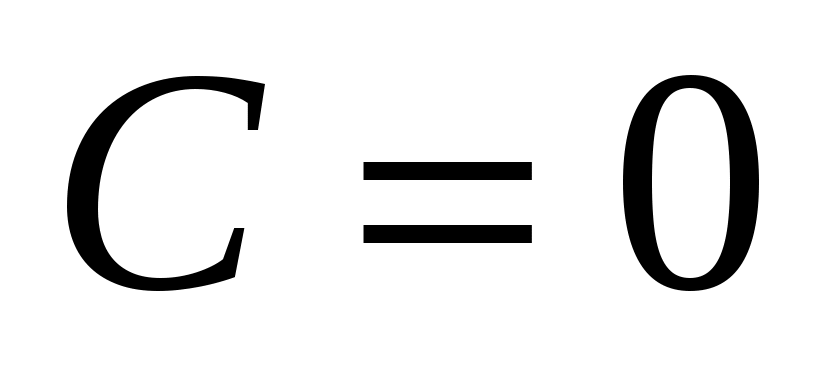 , , 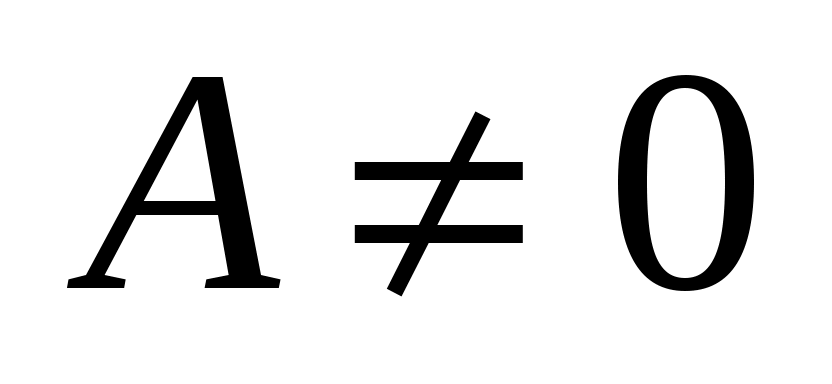 , , 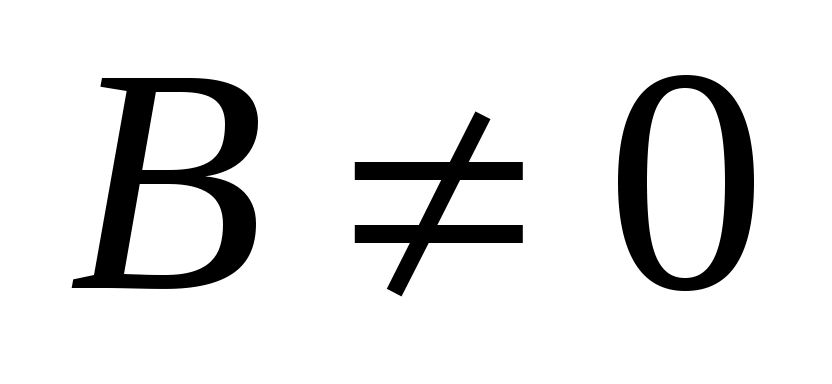 ; 2) ; 2) 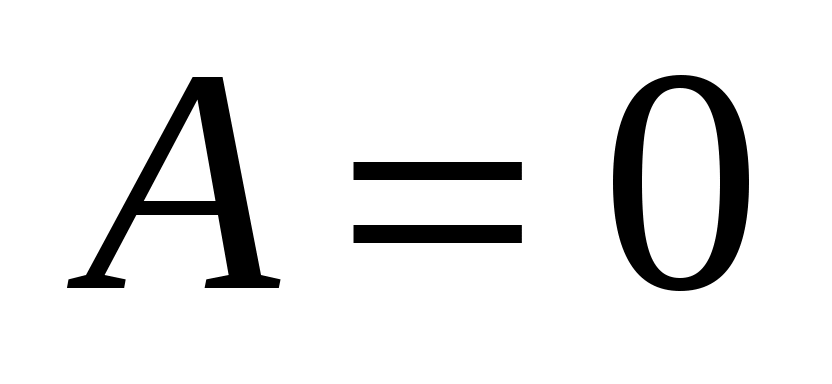 , , 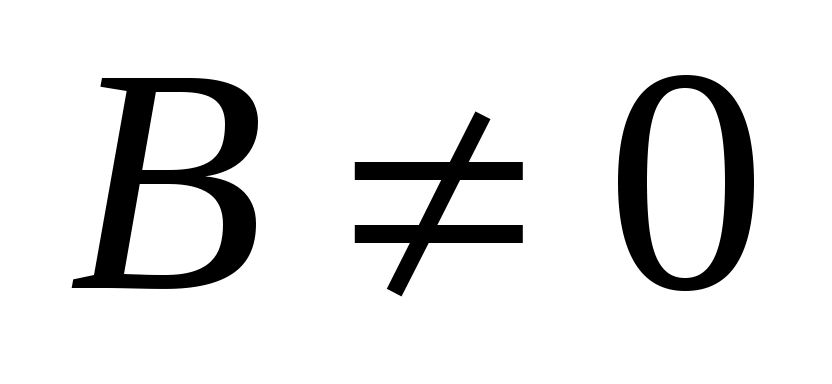 , , 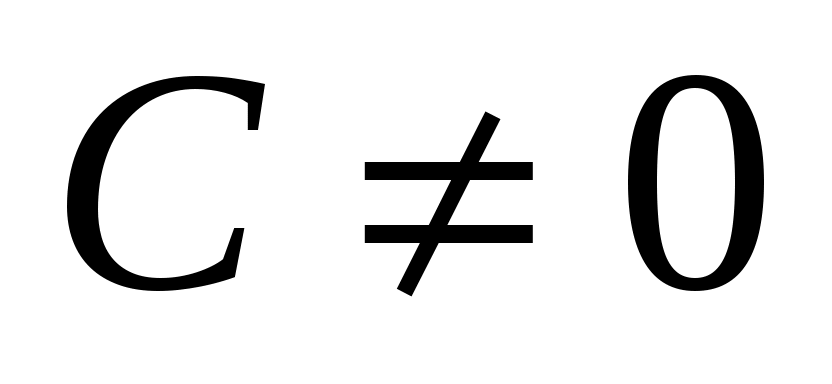 ; ;
3)  , , 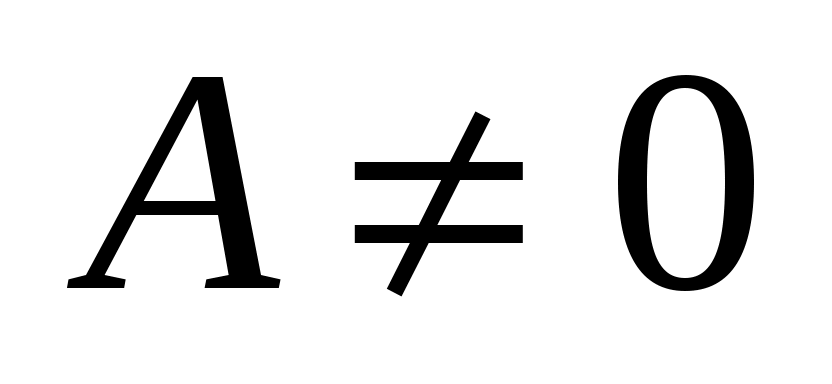 , , 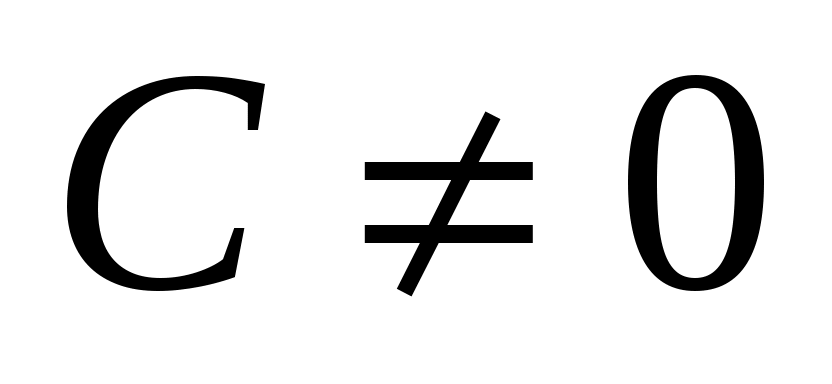 ; 4) ; 4) 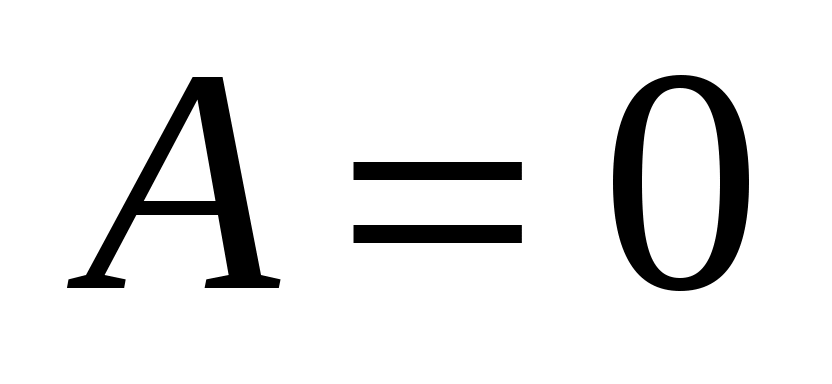 , , 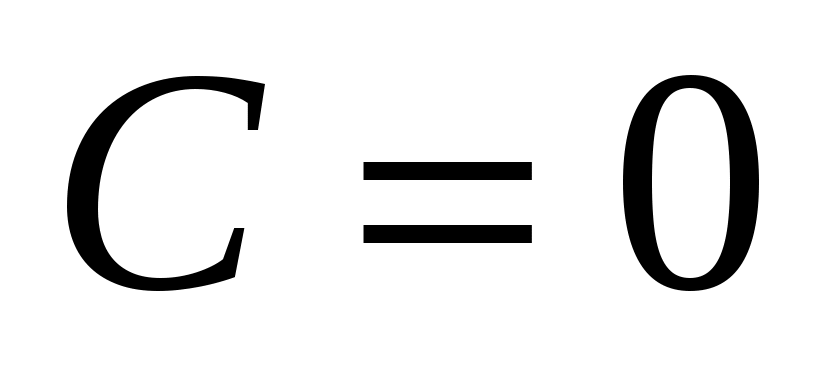 , , 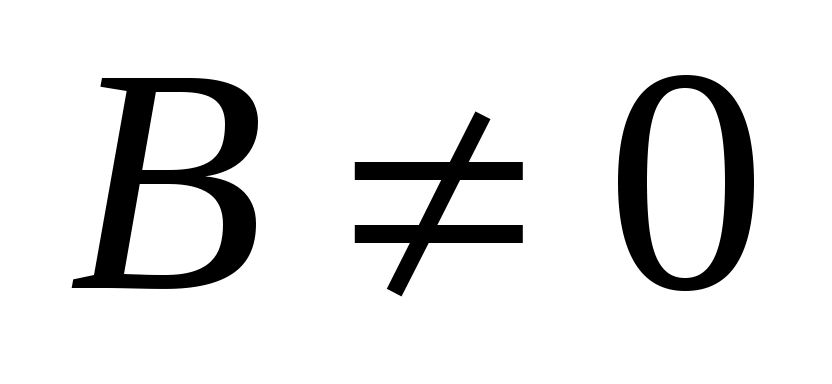 ; ;
5)  , ,  , , 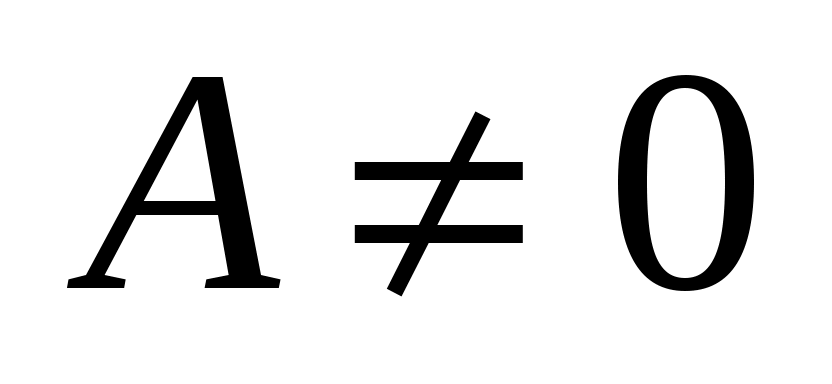 . .
Замечание. Два уравнения
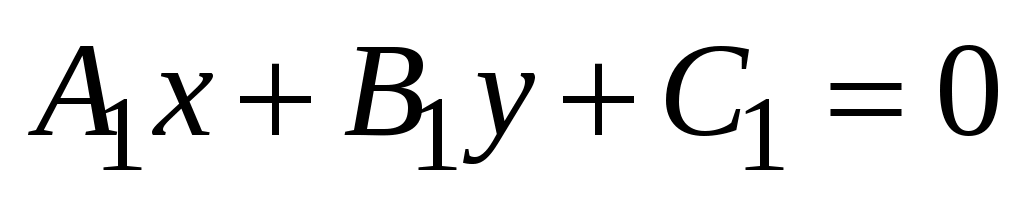 , (3.7) , (3.7)
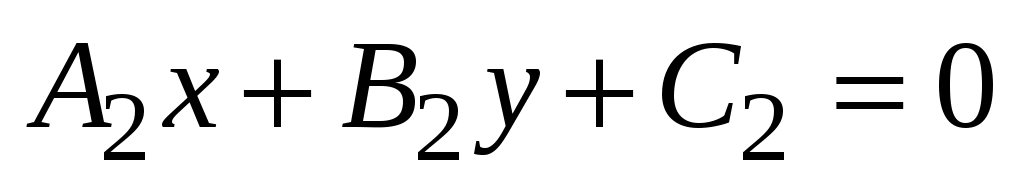 (3.8) (3.8)
определяют одну и ту же прямую тогда и только тогда, когда
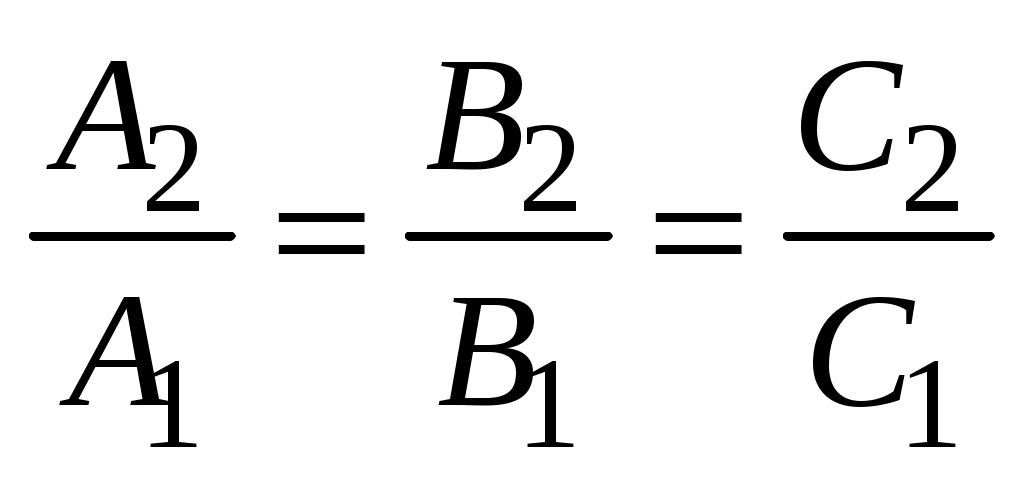 . (3.9) . (3.9)
Действительно, пусть (3.7) и (3.8) определяют одну и ту же прямую   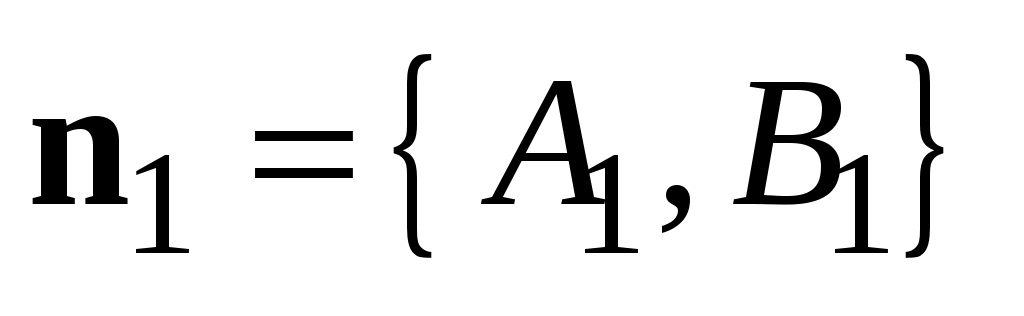 и и 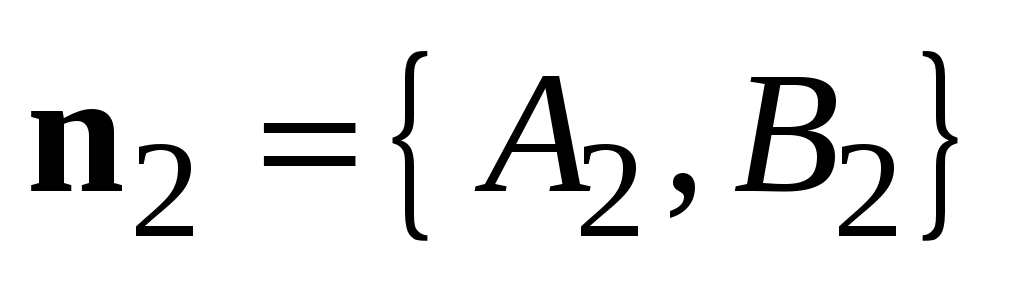 коллинеарны коллинеарны   . .
Обозначим это общее отношение через  : : 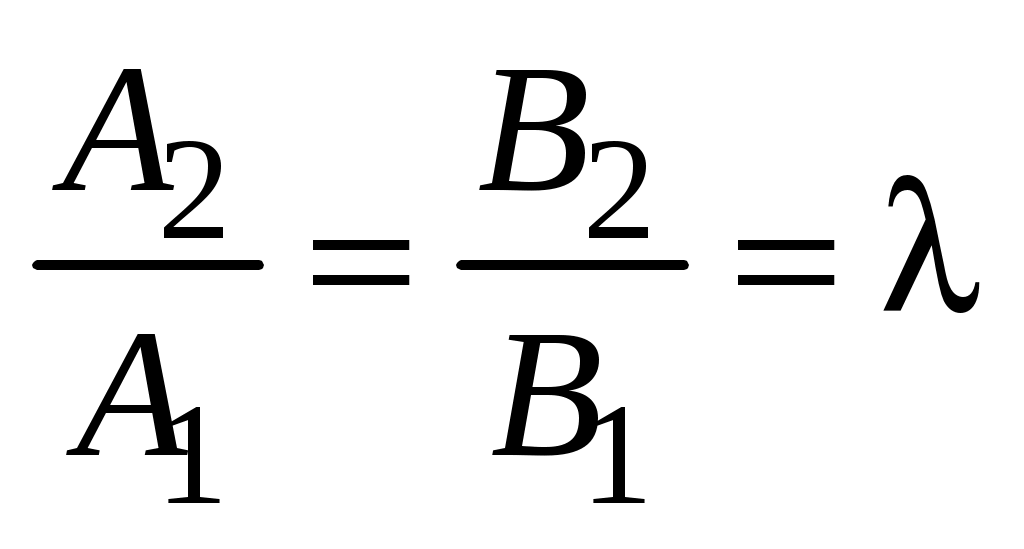 . .
Пусть 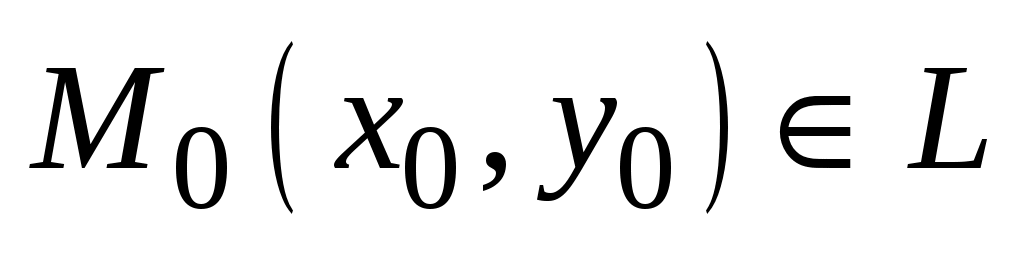 . Тогда выполняются два тождества: . Тогда выполняются два тождества:  и и 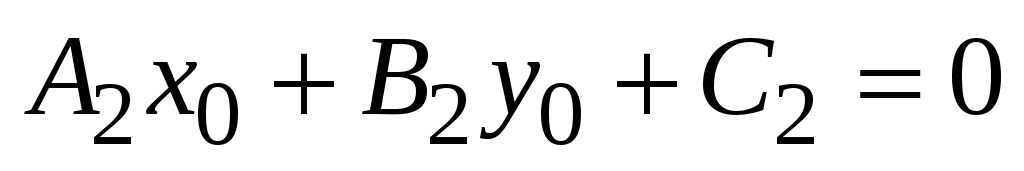 . .
Умножим первое на  и вычтем из второго: и вычтем из второго:
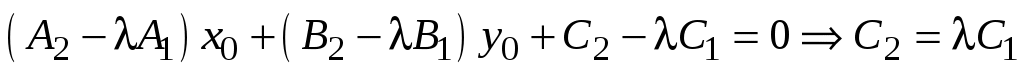 и и 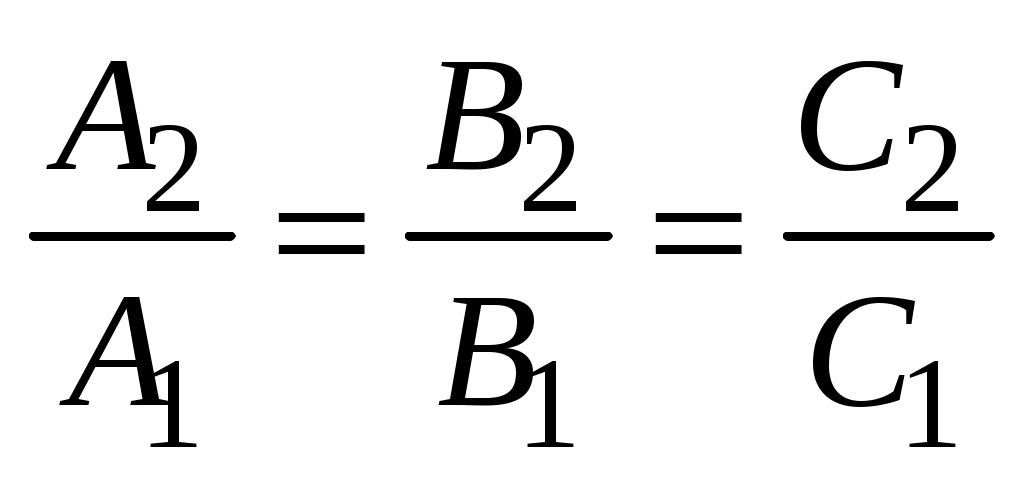 . .
Обратно. Пусть (3.7) определяет 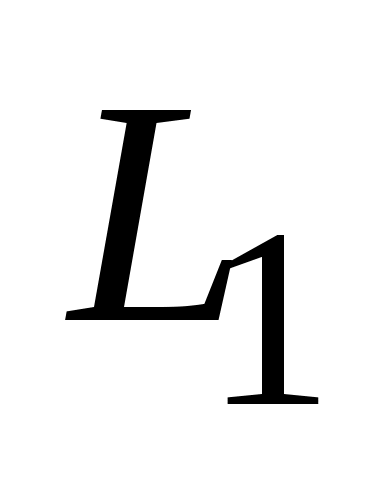 , а (3.8) - , а (3.8) -  и пусть выполняется равенство (3.9). Пусть и пусть выполняется равенство (3.9). Пусть  , следовательно, справедливо тождество , следовательно, справедливо тождество
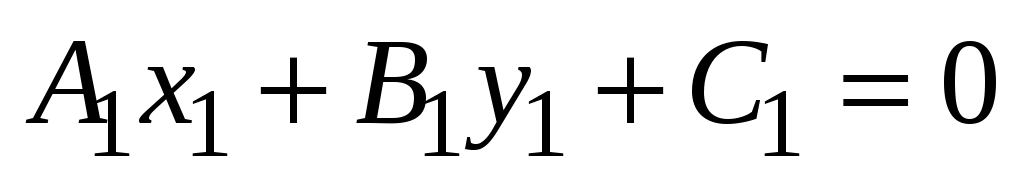 . (3.10) . (3.10)
Умножим обе части (3.10) на  и получим и получим 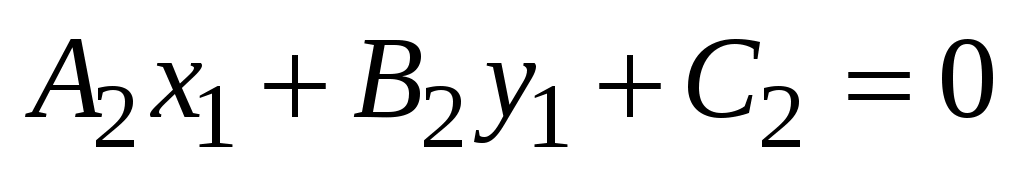 – это означает, что – это означает, что  . Справедливо также, что всякая точка . Справедливо также, что всякая точка  , принадлежащая , принадлежащая  , принадлежит , принадлежит 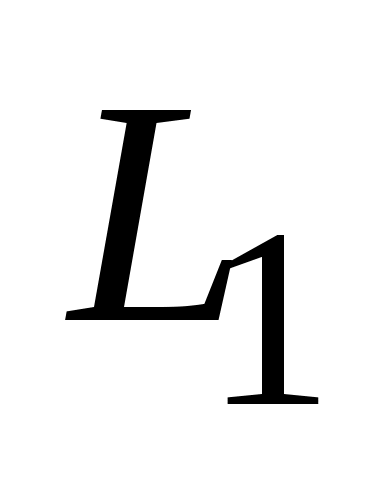 (доказывается совершенно аналогично) (доказывается совершенно аналогично)  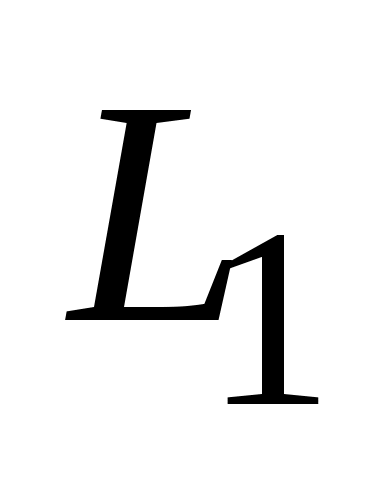 и и  состоят из одних и тех же точек состоят из одних и тех же точек  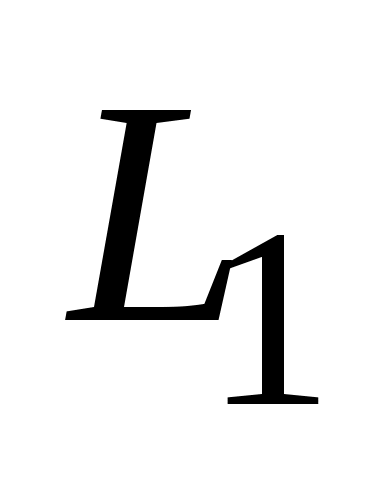 и и  совпадают. совпадают.
|
|
|
 Скачать 0.84 Mb.
Скачать 0.84 Mb. (рис. 3.1), или
(рис. 3.1), или  аким образом, если пара чисел
аким образом, если пара чисел 