|
|
лекция. Прямая на плоскости
3.3. Каноническое и параметрические уравнения прямой
Определение 4. Пусть 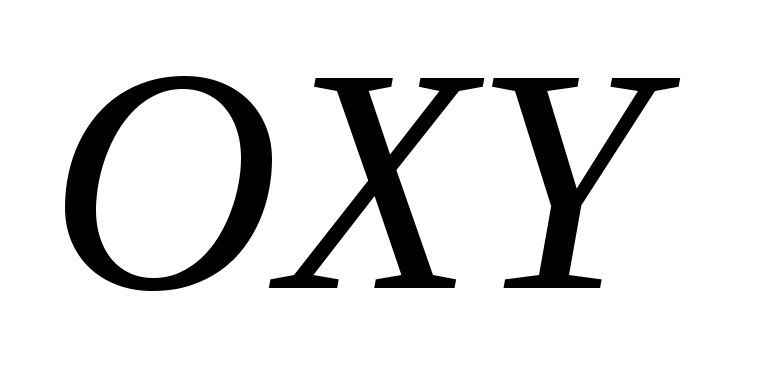 – декартова система координат, – декартова система координат,  - произвольная прямая. Любой вектор - произвольная прямая. Любой вектор  такой, что такой, что  , ,  параллелен параллелен  , называется направляющим вектором прямой , называется направляющим вектором прямой  (рис. 3.3). (рис. 3.3).

Пусть 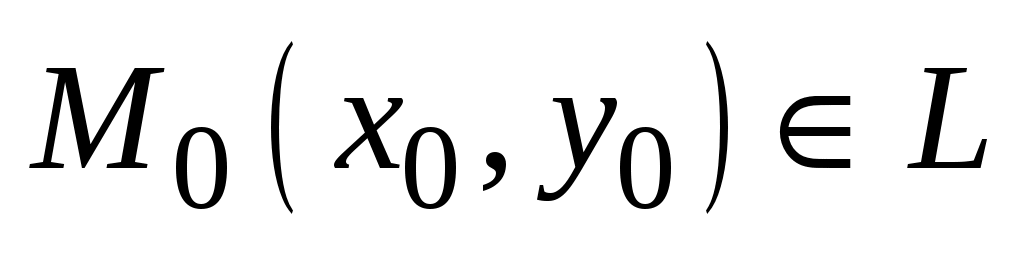 , , 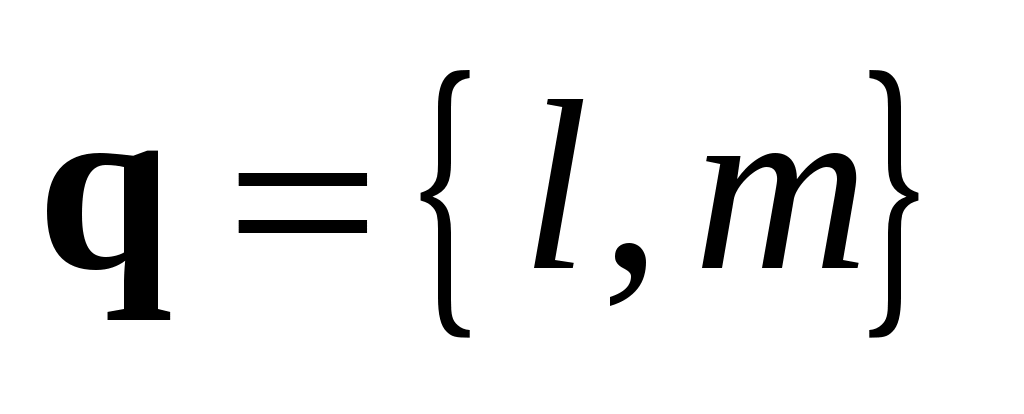 – направляющий вектор прямой – направляющий вектор прямой  . Тогда . Тогда
 коллинеарен коллинеарен 
  (3.11) (3.11)
(соответствующие координаты векторов  и и 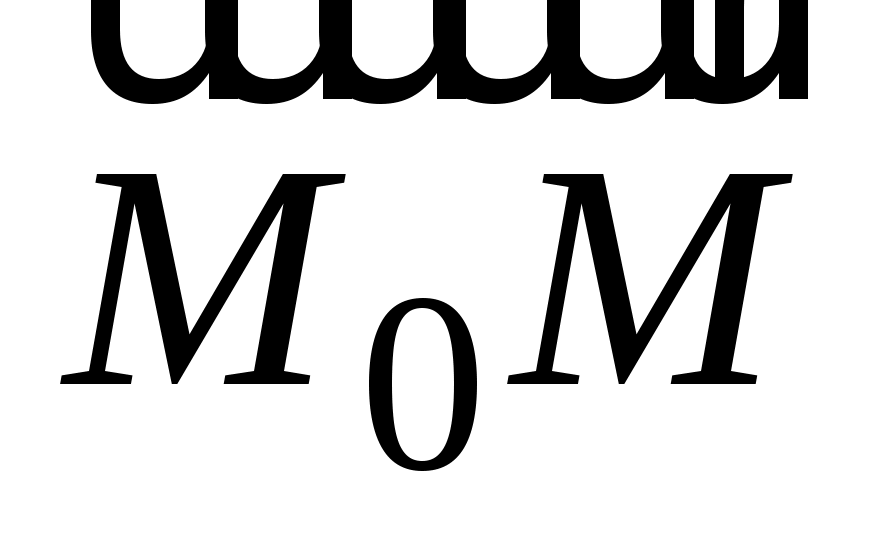 пропорциональны). пропорциональны).
Уравнение (3.11) называется каноническим уравнением прямой  , проходящей через точку , проходящей через точку  и имеющей направляющим вектор и имеющей направляющим вектор 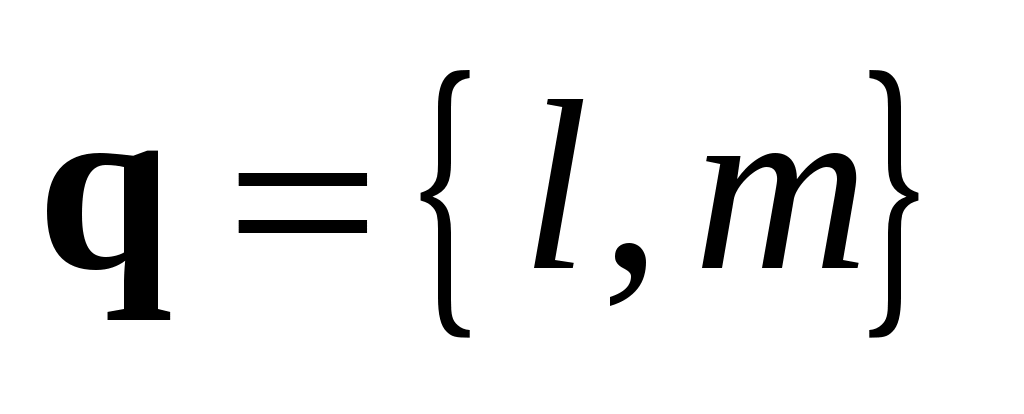 . .
Обозначим отношение в (3.11) через  : : 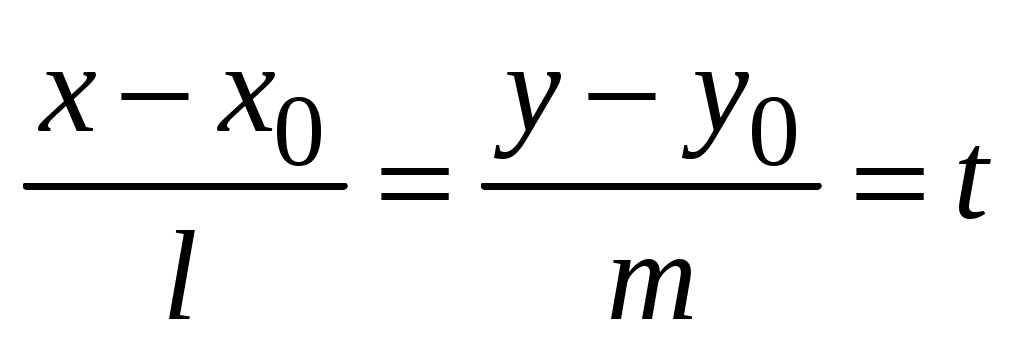 . Тогда уравнение (3.11) приведет к двум равенствам . Тогда уравнение (3.11) приведет к двум равенствам
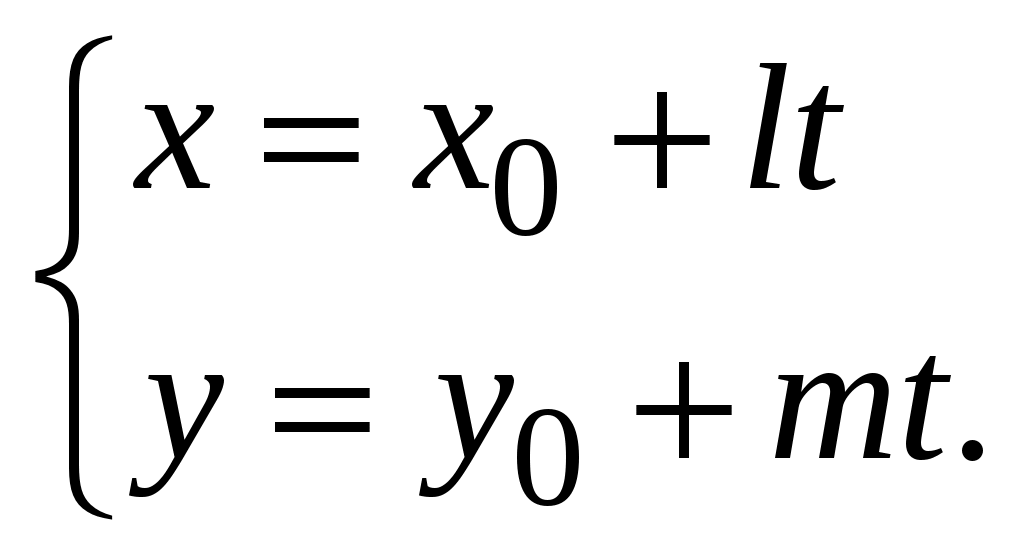 (3.12) (3.12)
Так как  , то хотя бы одно из чисел , то хотя бы одно из чисел 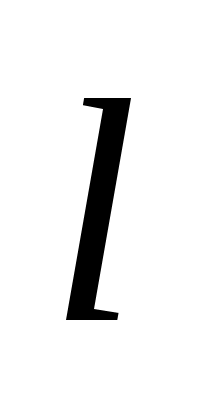 или или 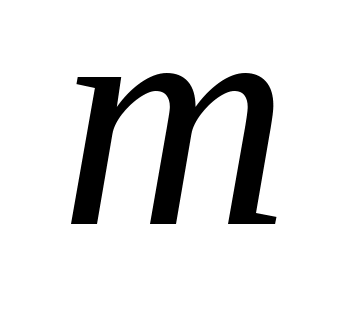 отлично от нуля. Пусть для определенности отлично от нуля. Пусть для определенности 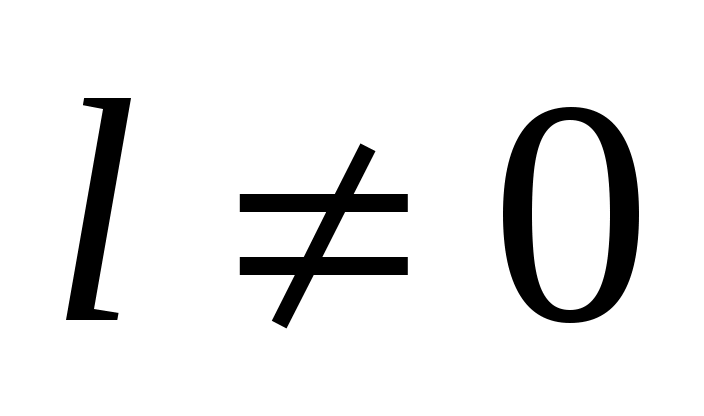 . Тогда при . Тогда при 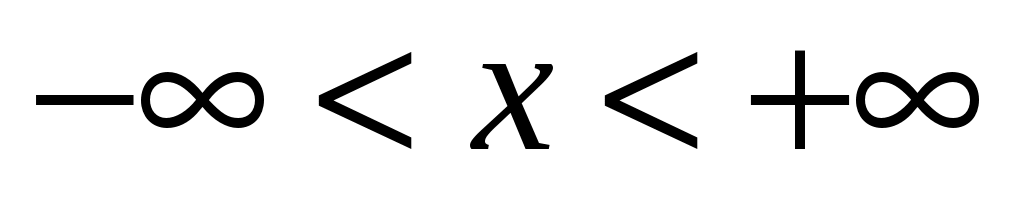 и и  , таким образом, , таким образом, 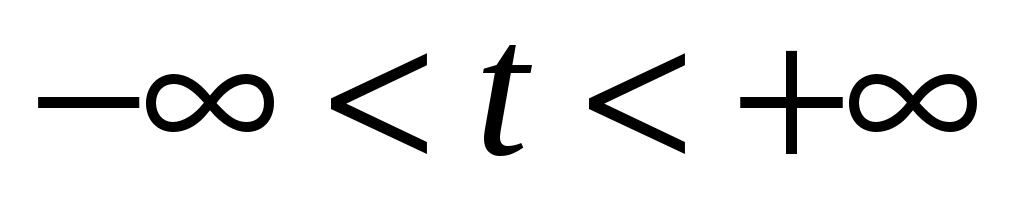 . .
Равенства (3.12) при 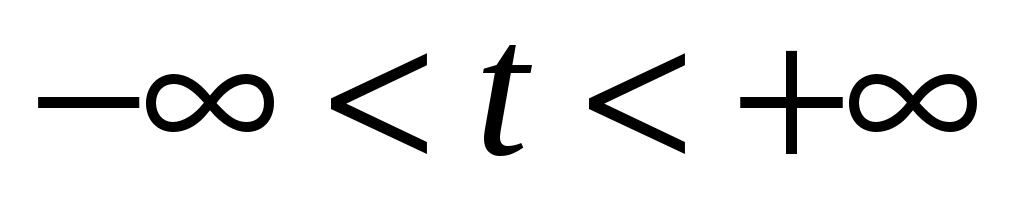 называются параметрическими уравнениями прямой называются параметрическими уравнениями прямой  , проходящей через точку , проходящей через точку  и имеющей в качестве направляющего вектор и имеющей в качестве направляющего вектор 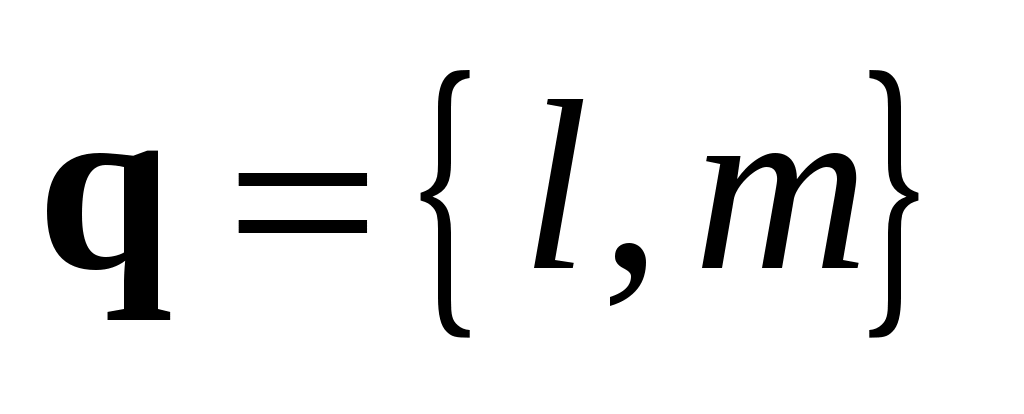 . .
Пример 2. Составить каноническое уравнение прямой  , проходящей через две заданные точки , проходящей через две заданные точки  и и  . .
В качестве направляющего возьмем вектор  (рис. 3.4). Воспользуемся уравнением (3.11), полагая (рис. 3.4). Воспользуемся уравнением (3.11), полагая 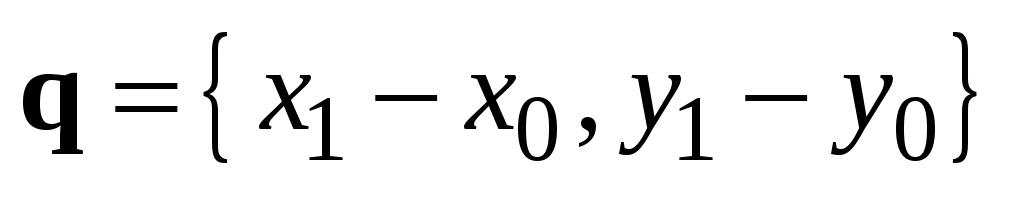 , и получим , и получим
 . (3.13). . (3.13).
Пример 3. Составить каноническое уравнение прямой  , проходящей через , проходящей через 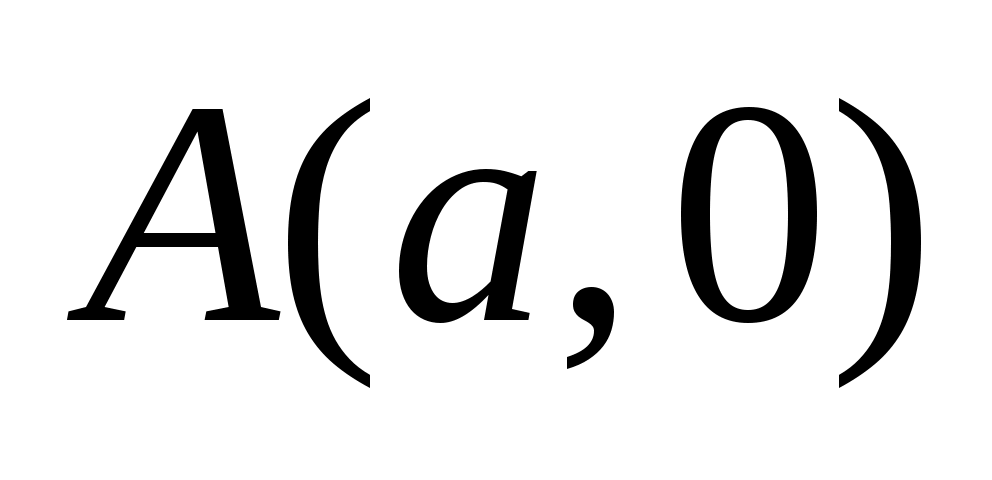 и и  ( (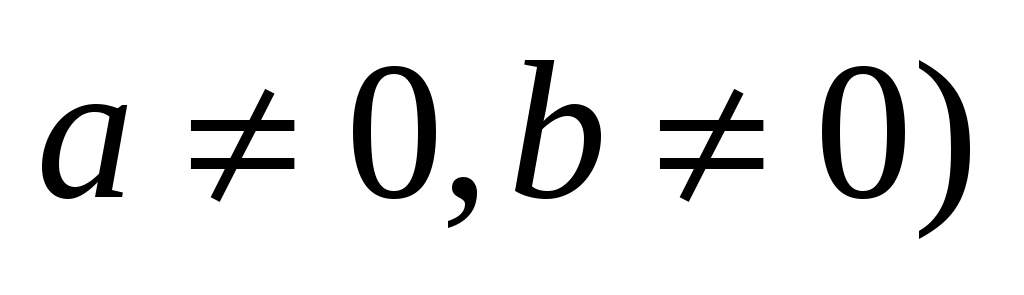 (рис. 3.5). (рис. 3.5).
Воспользуемся уравнением (3.13), полученным в примере 2, считая 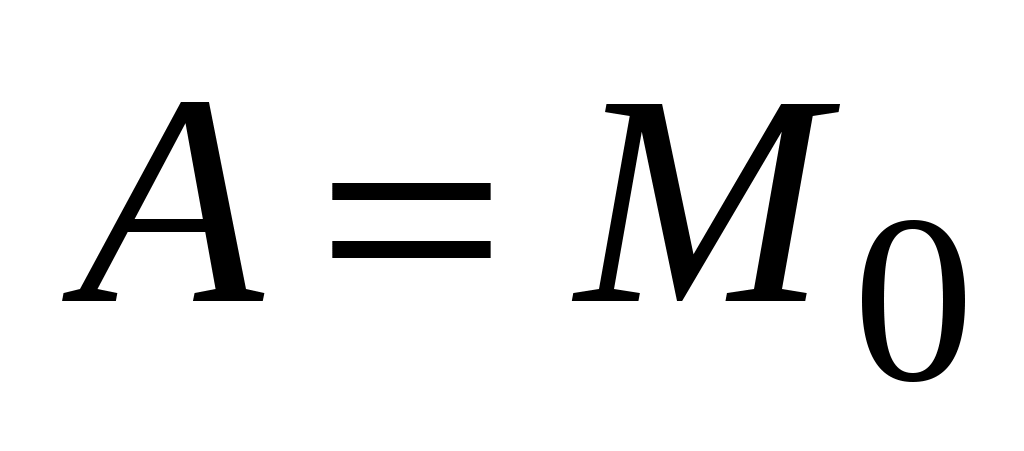 , , 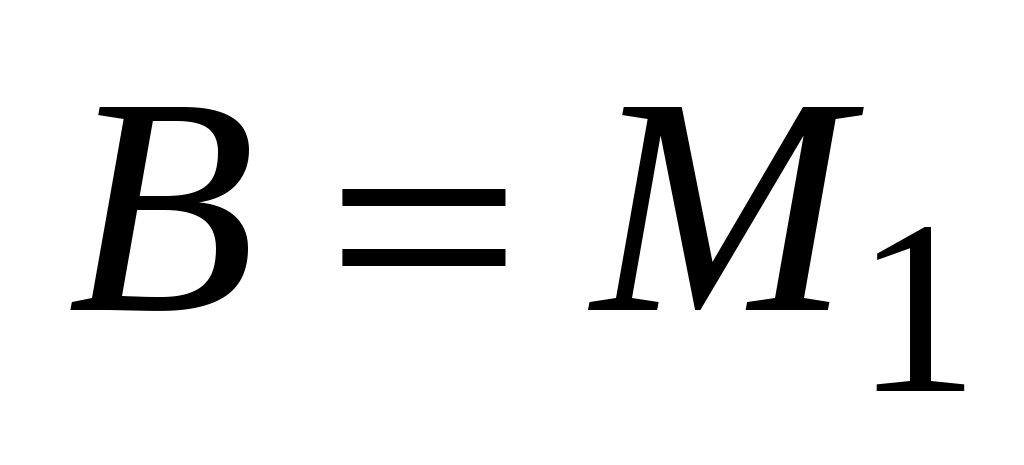 : : 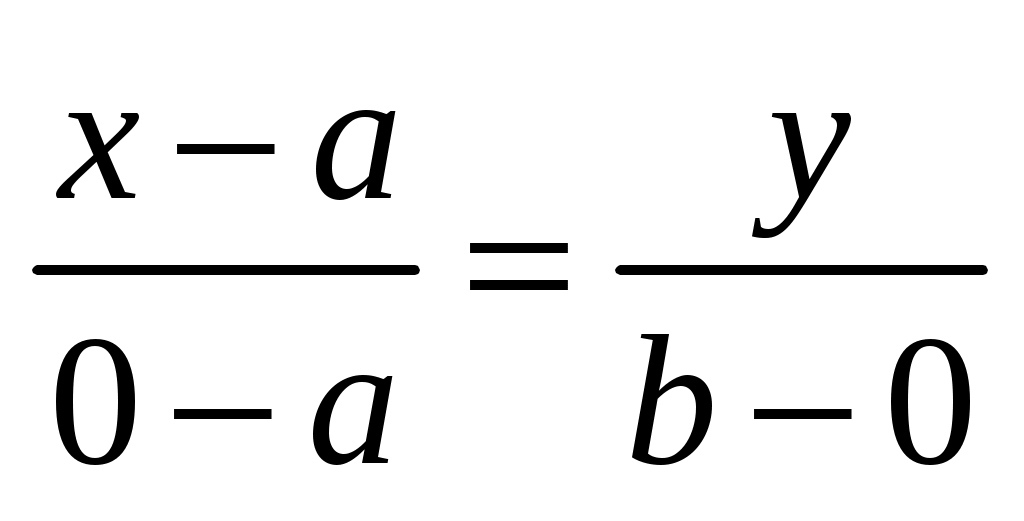 , или , или
 . (3.14) . (3.14)
Уравнение (3.14) называется уравнением прямой в отрезках.
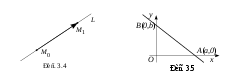
3.4. Уравнение прямой с угловым коэффициентом
О пределение 5. Пусть пределение 5. Пусть  – декартова система координат, – декартова система координат,  не параллельна оси не параллельна оси  и пересекает ее в точке и пересекает ее в точке  (рис. 3.6). Выберем на оси (рис. 3.6). Выберем на оси  точку точку  , расположенную по ту сторону от , расположенную по ту сторону от  куда направлена ось куда направлена ось 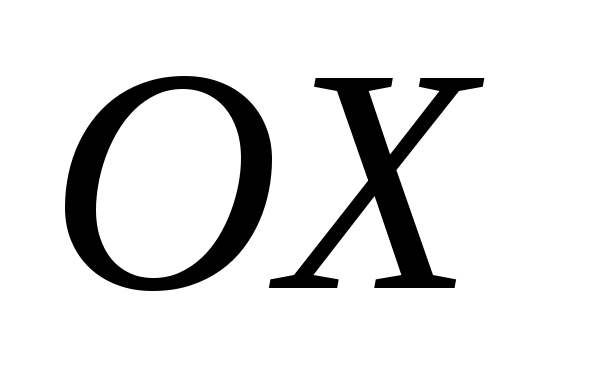 . На . На  выберем точку выберем точку 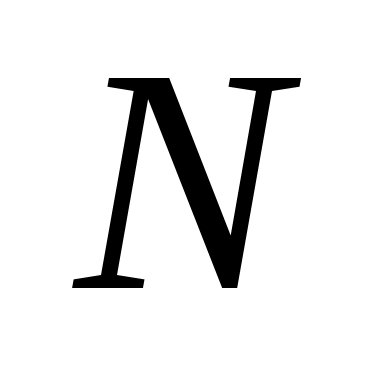 , расположенную на прямой , расположенную на прямой  по ту сторону от по ту сторону от  , куда направлена ось , куда направлена ось 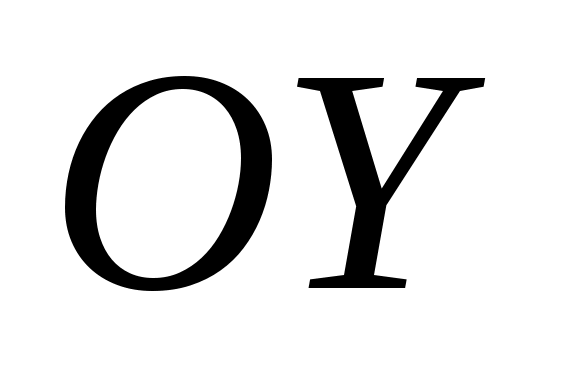 . Угол . Угол  называется углом наклона прямой называется углом наклона прямой  к оси к оси 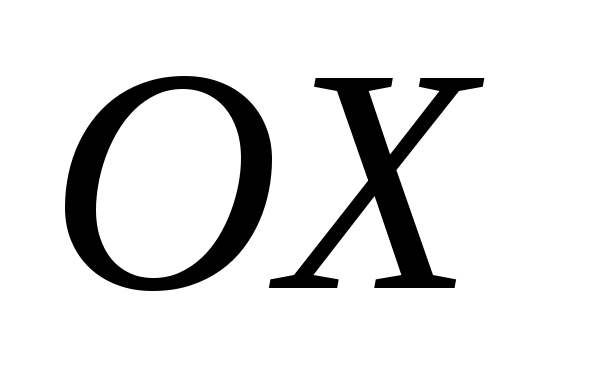 . Число . Число  называется угловым коэффициентом прямой называется угловым коэффициентом прямой  (если (если  параллельна оси параллельна оси 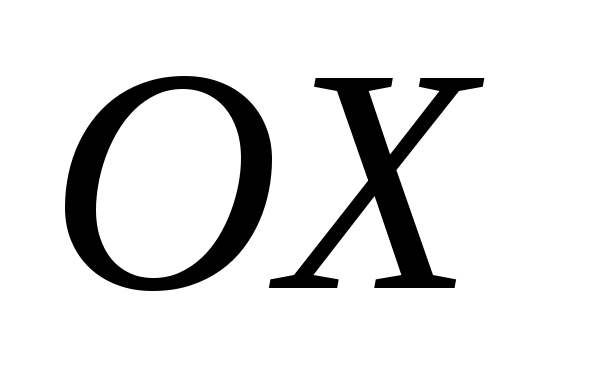 , то , то 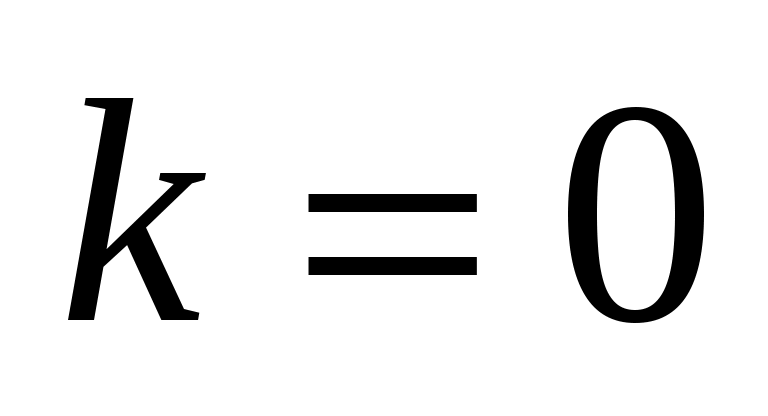 ; если ; если 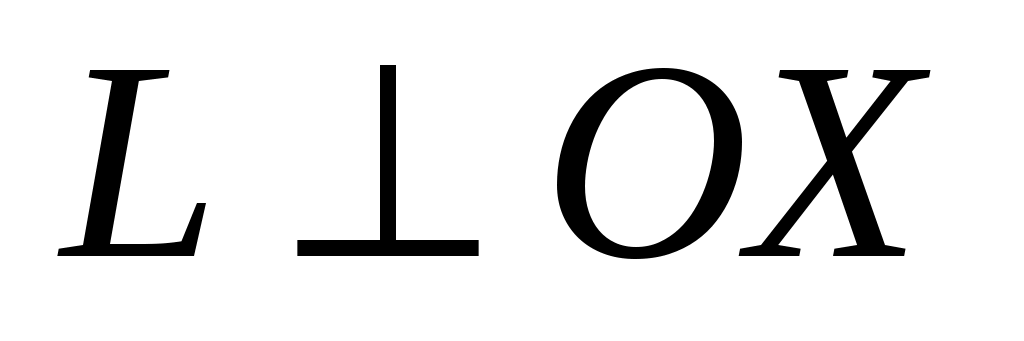 , т.е. , т.е.  параллельна параллельна 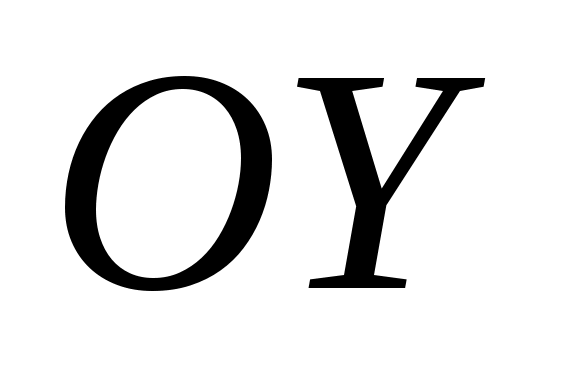 , то , то 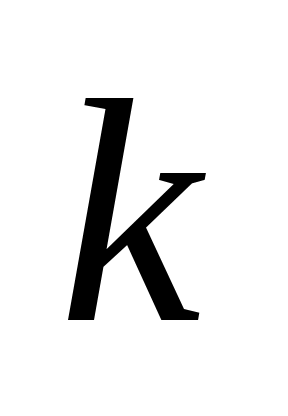 не определен). не определен).
Упражнение. Доказать следующее утверждение: пусть  не параллельна оси не параллельна оси  , , 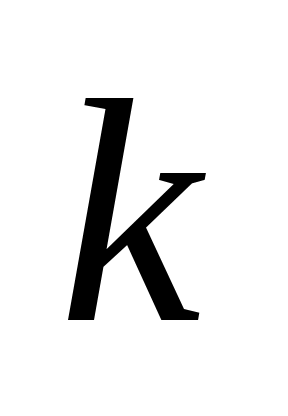 – угловой коэффициент – угловой коэффициент  , , 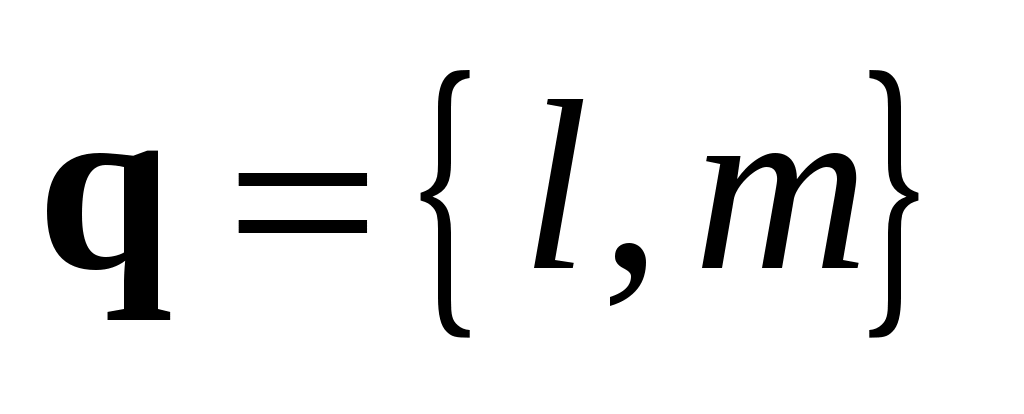 – направляющий вектор прямой – направляющий вектор прямой  , тогда , тогда 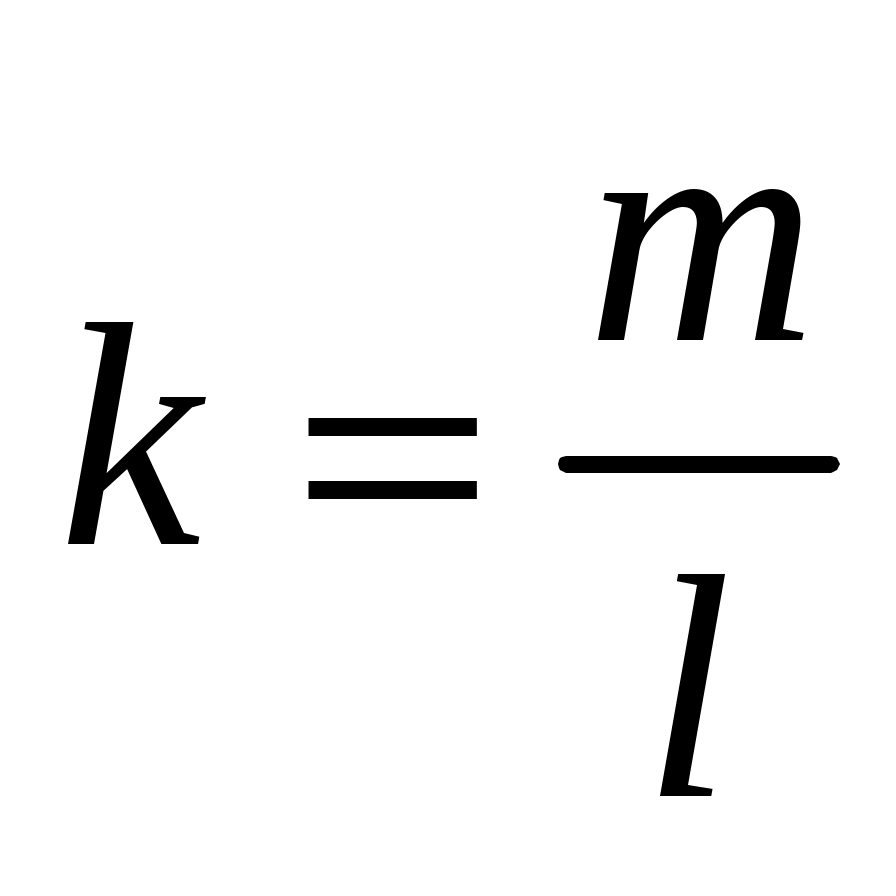 . .
Пример 4. Пусть 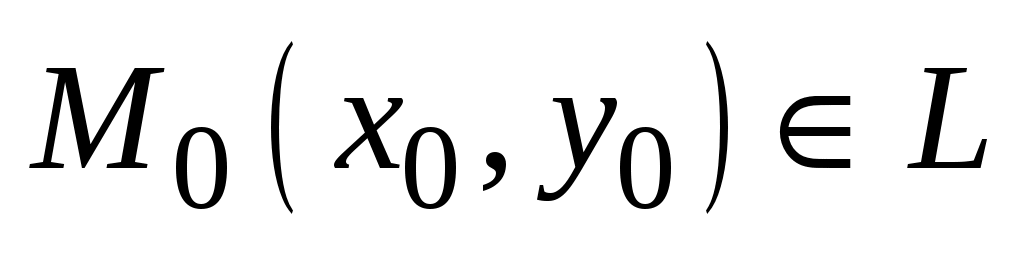 , , 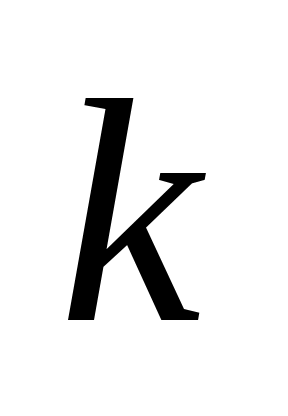 – угловой коэффициент прямой – угловой коэффициент прямой  . Составить уравнение прямой. . Составить уравнение прямой.
Воспользуемся каноническим уравнением (3.11):
 , или , или 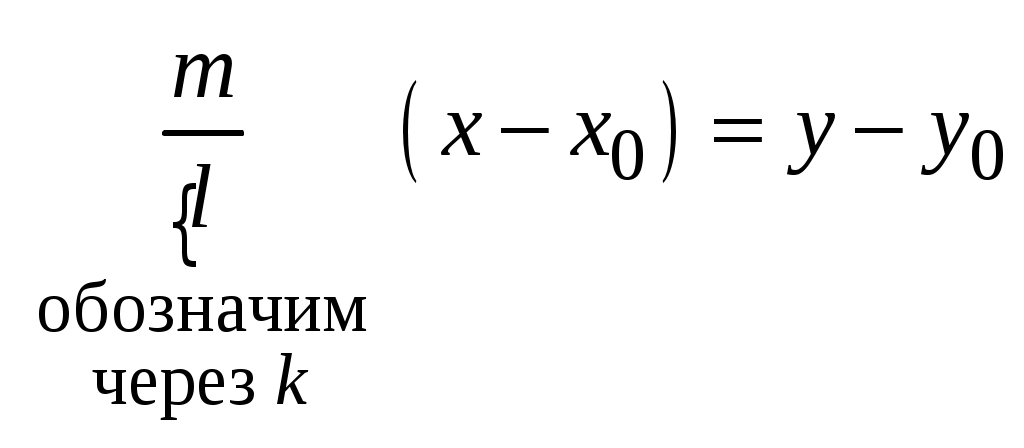 , или , или 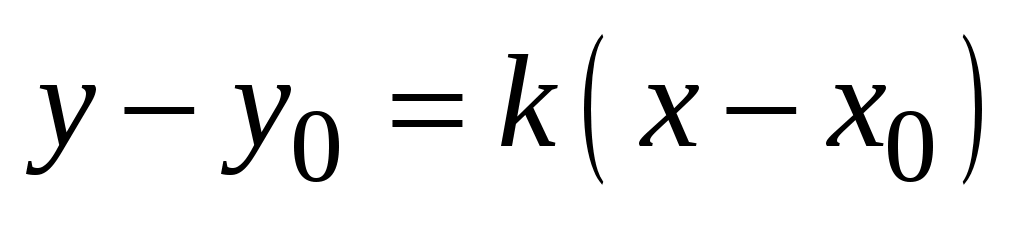 , или , или  , ,
или  . (3.15) . (3.15)
Уравнение (3.15) называется уравнением прямой с угловым коэффициентом (в уравнении (3.15) 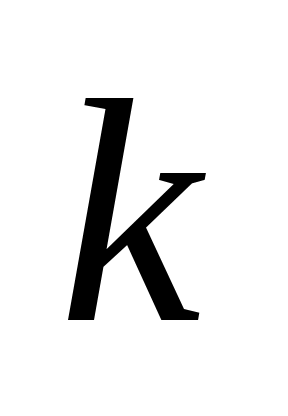 – угловой коэффициент прямой (см. упражнение), а – угловой коэффициент прямой (см. упражнение), а 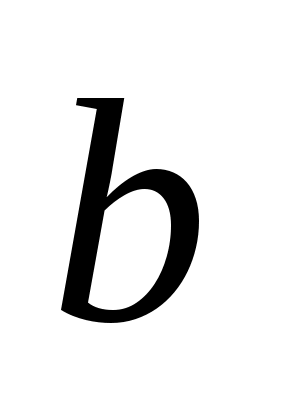 – ордината точки пересечения прямой с осью – ордината точки пересечения прямой с осью 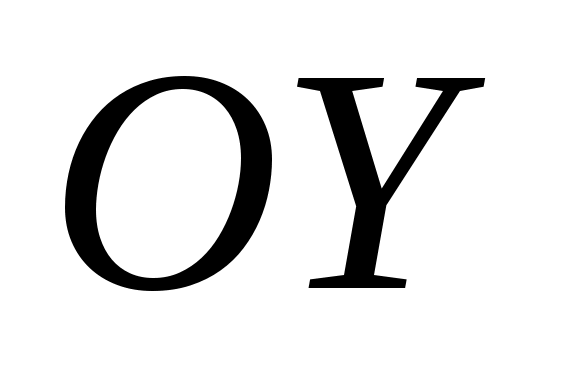 ). ).
Итак, положение прямой  на плоскости полностью определяется заданием: на плоскости полностью определяется заданием:
точки 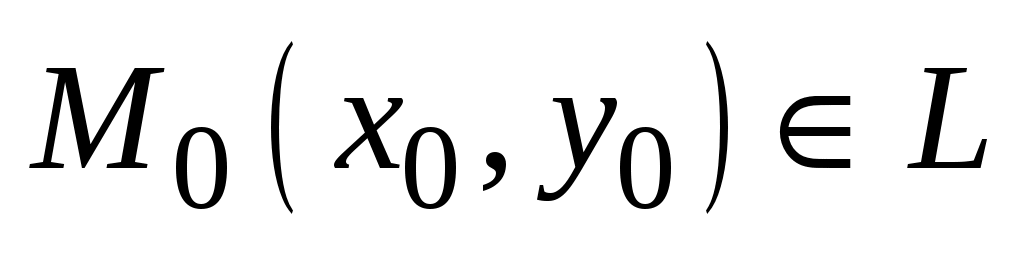 и и 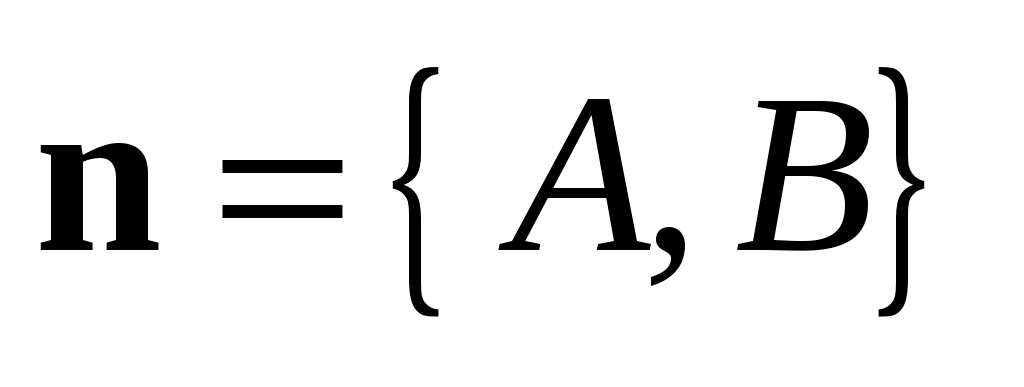 , перпендикулярного прямой , перпендикулярного прямой  (нормального вектора); (нормального вектора);
точки 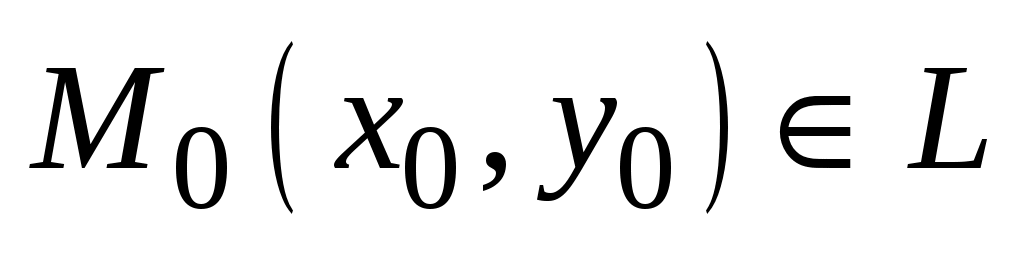 и вектора и вектора 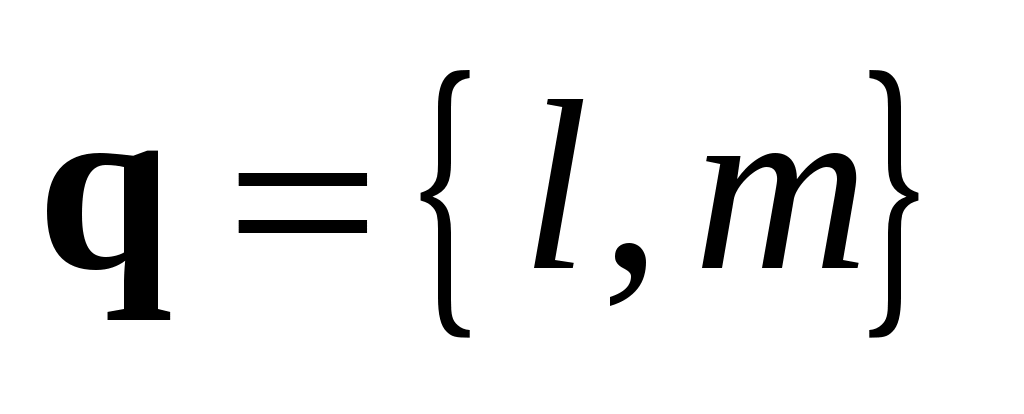 , параллельного прямой , параллельного прямой  (направляющего вектора); (направляющего вектора);
точки 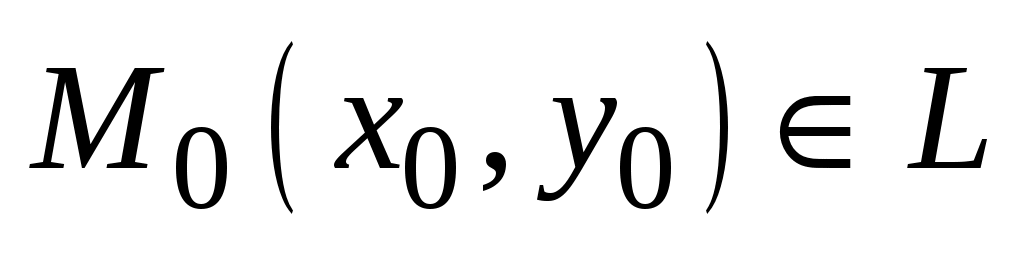 и углового коэффициента и углового коэффициента 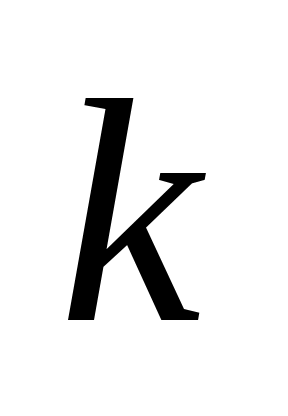 . .
3.5. Угол между двумя прямыми
Две прямые 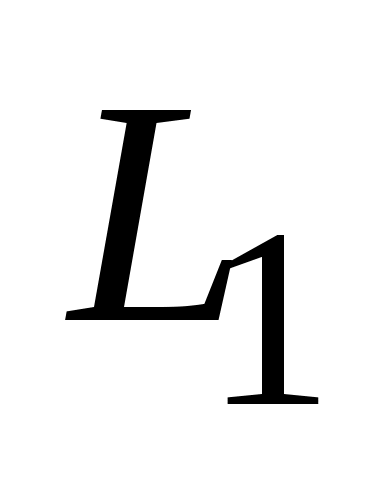 и и  , пересекаясь, образуют два угла, дополняющие друг друга до , пересекаясь, образуют два угла, дополняющие друг друга до  . Любой из этих углов будем считать углом между прямыми . Любой из этих углов будем считать углом между прямыми 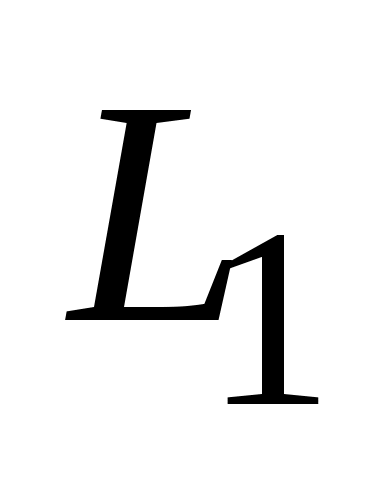 и и  и обозначать далее и обозначать далее  . .
Утверждение 1. Пусть прямые  и и  заданы своими общими уравнениями заданы своими общими уравнениями
 : : 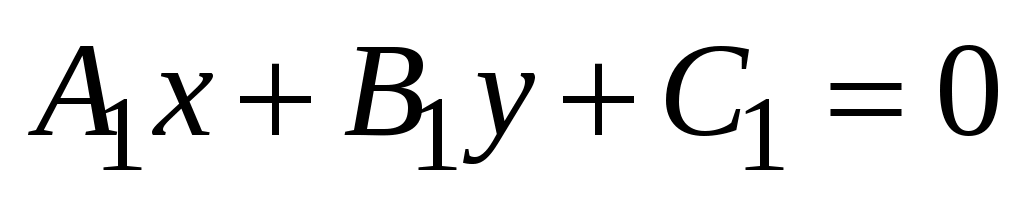 и и  : : 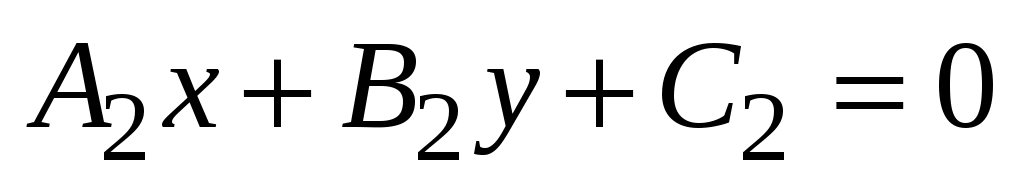 . .
Тогда
 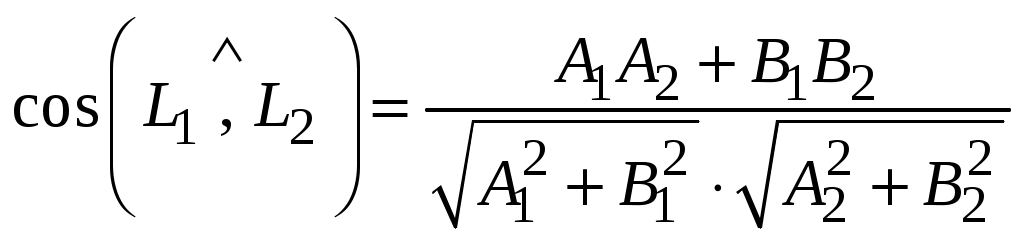 . (3.16) . (3.16)
В самом деле, один из углов между 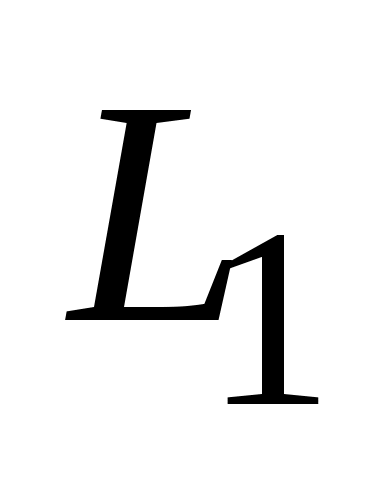 и и  равен углу между нормальными векторами равен углу между нормальными векторами  и и 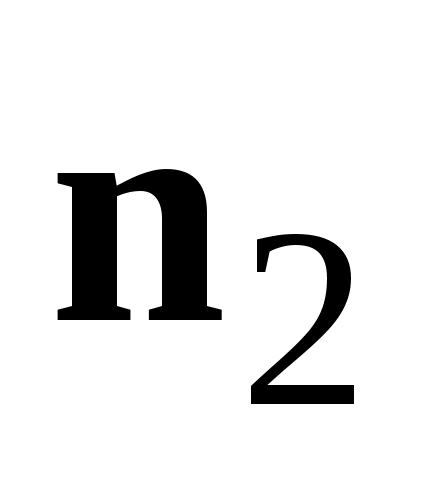 (рис.3.7). (Углы, отмеченные двумя дугами, равны как углы с соответственно перпендикулярными сторонами.) (рис.3.7). (Углы, отмеченные двумя дугами, равны как углы с соответственно перпендикулярными сторонами.)
Итак, 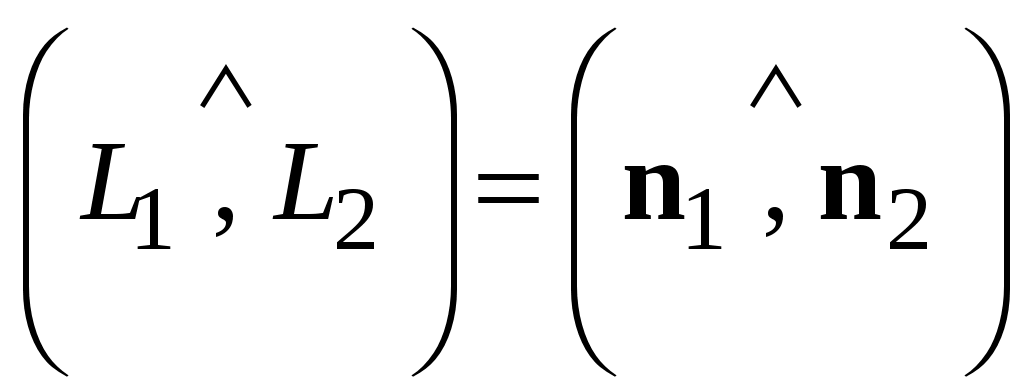 , отсюда , отсюда
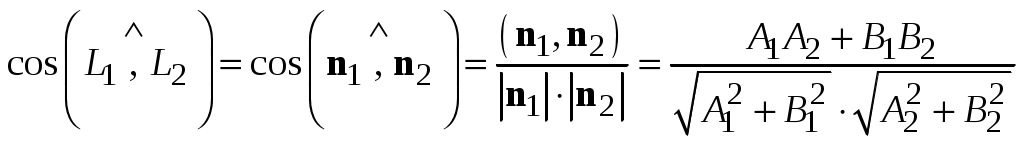 , ,
и формула (3.16) верна.
Отметим частные случаи:
1) 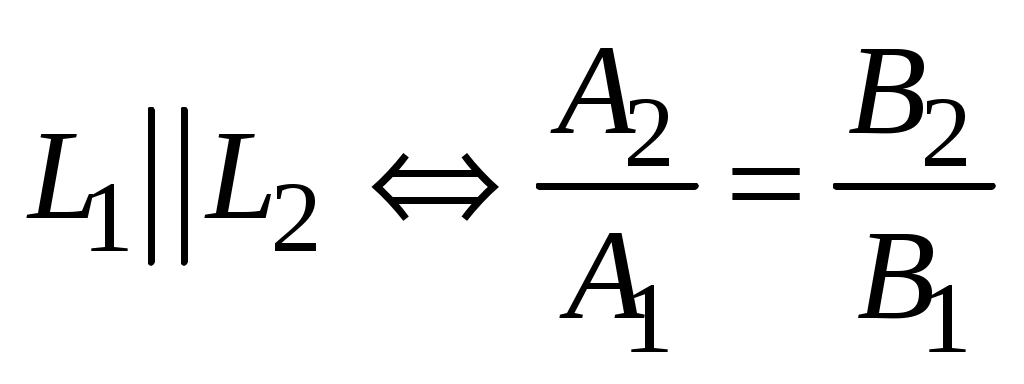 (условие коллинеарности (условие коллинеарности  и и  ) (рис. 3.8); ) (рис. 3.8);
2) 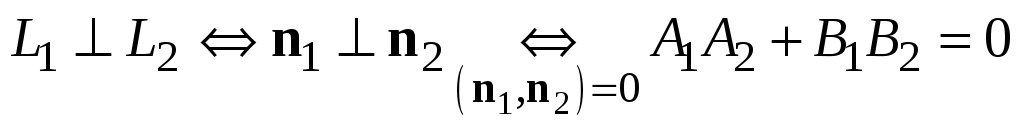 (рис. 3.9). (рис. 3.9).

Утверждение 2. Пусть прямые 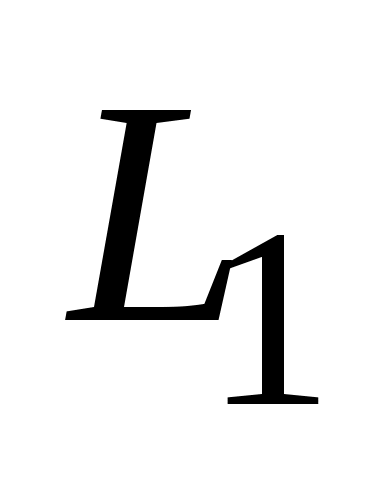 и и  заданы своими каноническими уравнениями заданы своими каноническими уравнениями
 : : 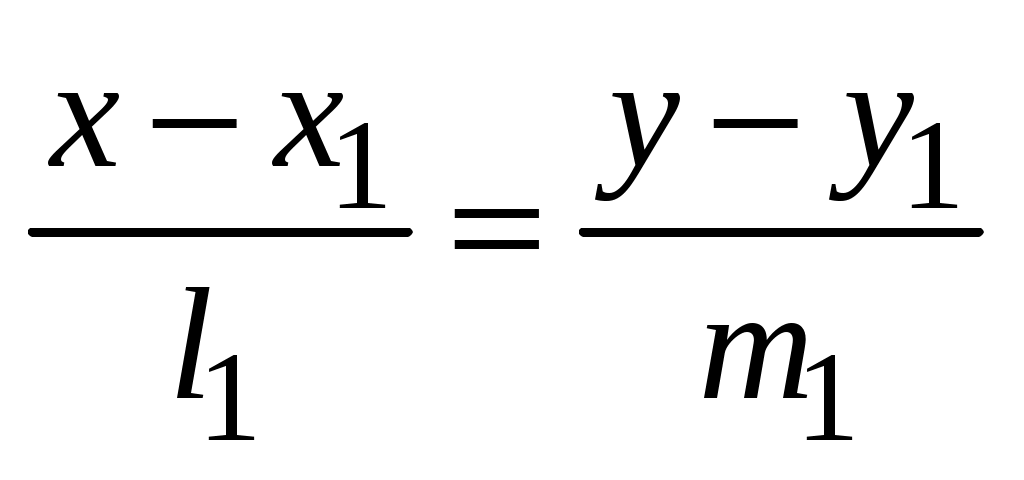 и и  : : 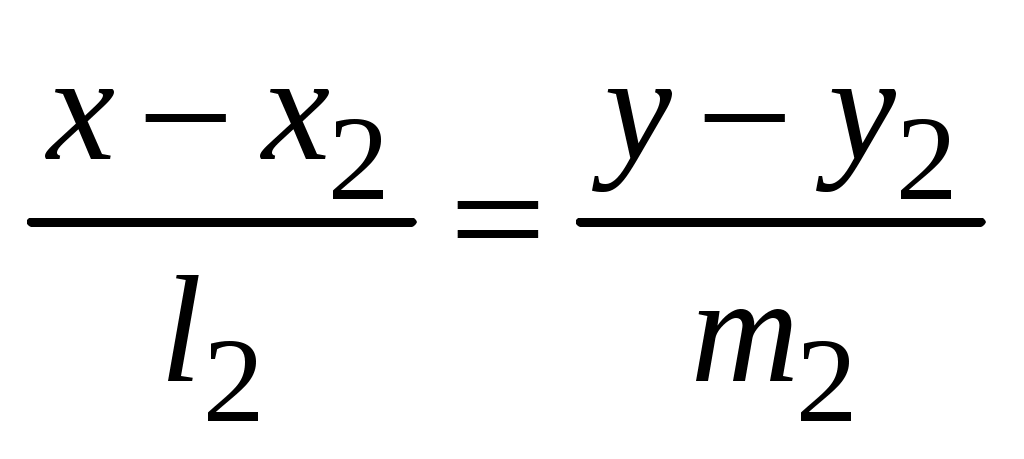 . .
Тогда
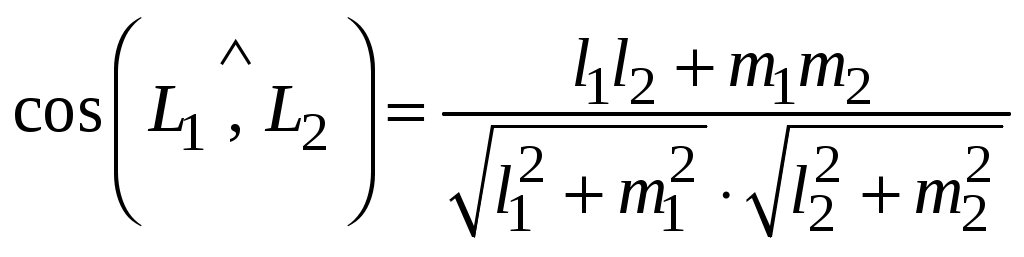 . (3.17) . (3.17)
Действительно, один из углов между прямыми 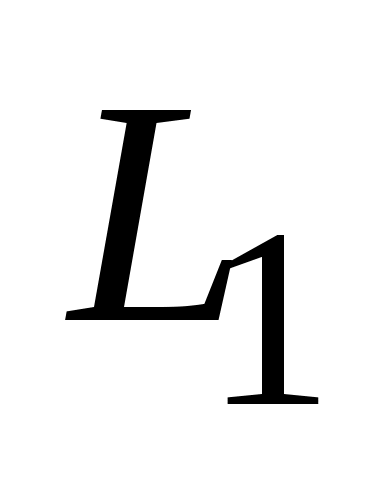 и и  равен углу между направляющими векторами равен углу между направляющими векторами 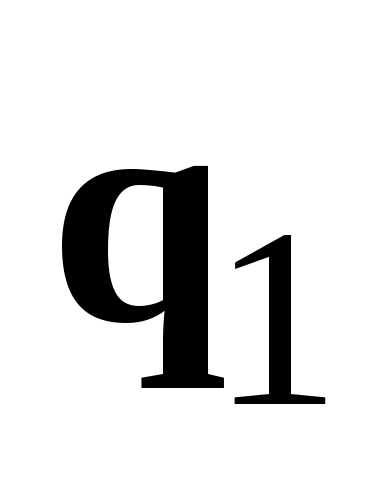 и и  (на рис. 3.10 отмечены одной дугой). (на рис. 3.10 отмечены одной дугой).

Итак,  , ,  , ,  , поэтому , поэтому
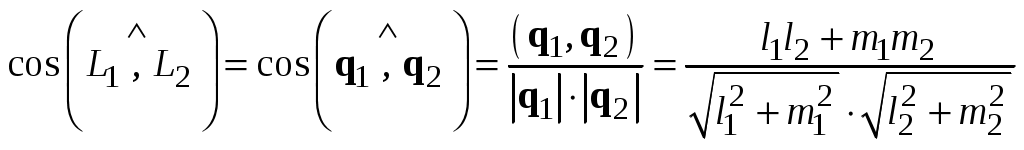 , ,
и равенство (3.17) справедливо.
Частные случаи:
1) 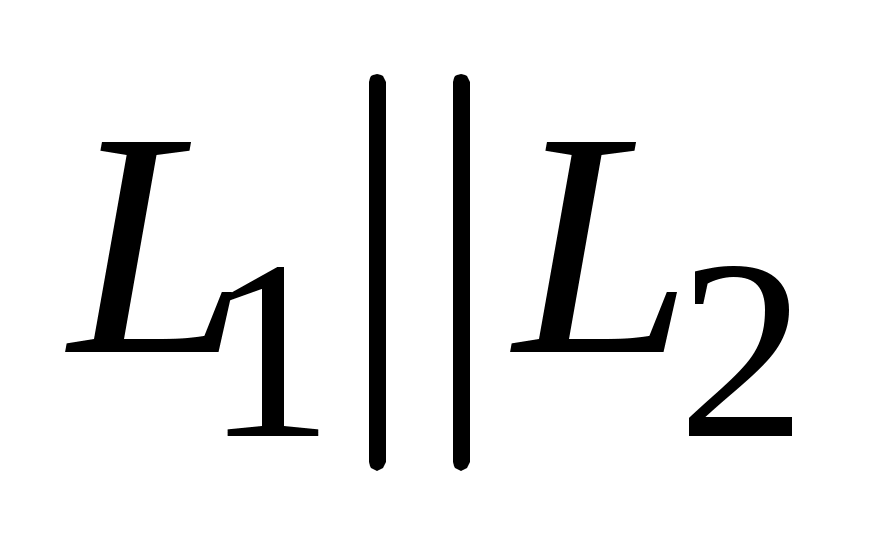  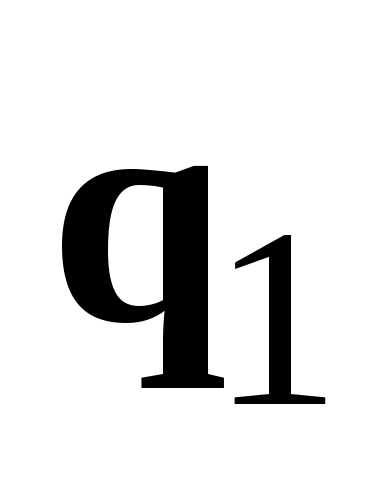 и и  коллинеарны коллинеарны 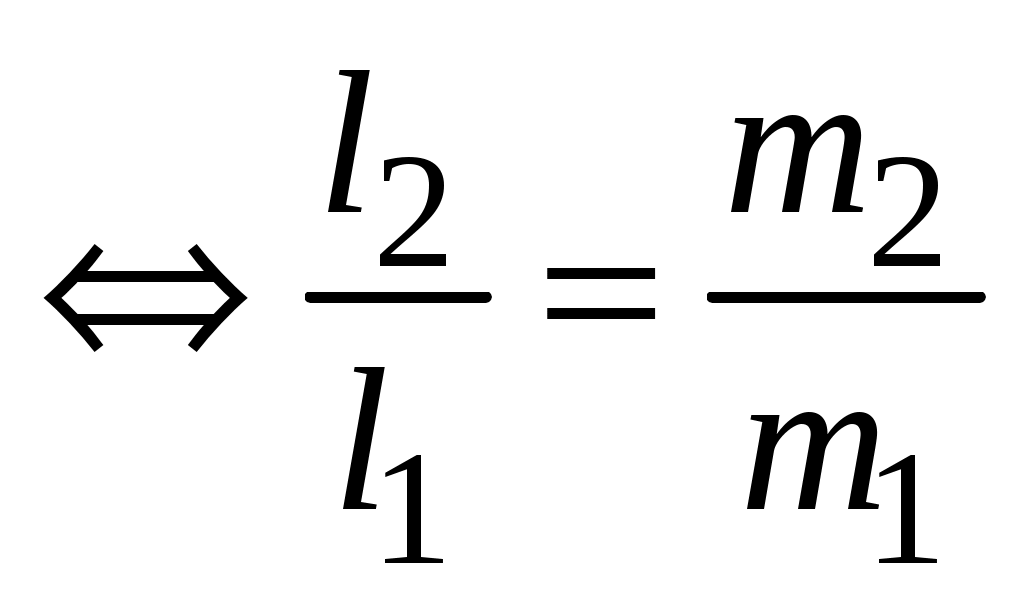 (рис. 3.11); (рис. 3.11);
2) 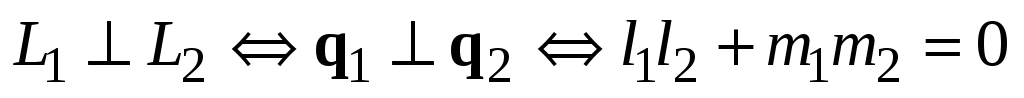 (рис. 3.12). (рис. 3.12).

|
|
|
 Скачать 0.84 Mb.
Скачать 0.84 Mb.
 пределение 5. Пусть
пределение 5. Пусть 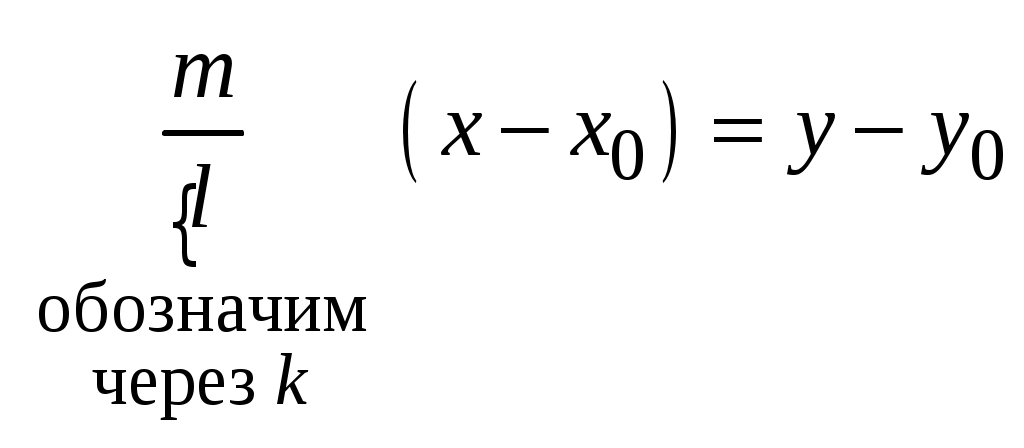 , или
, или 



