|
|
Рабочая программа по алгебре 7 класс. Рабочая программа по алгебре 7 класс Г. Магнитогорск, 2013 пояснительная записка
Тематическое планирование по алгебре для 7 класса
№ п/п
|
Количество часов на тему
|
Тема
|
Требования к уровню достижения
государственного образовательного стандарта
Знания, умения, навыки, типовые задания
|
Требования к уровню возможностей
Знания, умения, навыки,
задания продвинутого уровня
|
Повторение* *
|
Примечание* * *
|
1.
|
15
|
Математический язык. Математическая модель
|
Ученик должен знать:
Понятия: числовое выражение, значение числового выражения, алгебраическое выражение, значение алгебраического выражения, допустимое, недопустимое значение алгебраического выражения, математический язык, математическая модель;
Понятие линейного уравнения с одной переменной и алгоритм его решения;
Алгоритм решения задач с помощью уравнений выделяя три этапа математического моделирования;
Понятие: координатная прямая, обозначение числовых промежутков, название числовых промежутков.
Ученик должен уметь:
Находить значение числового выражения; составлять числовое выражение для решения задачи;
Записывать алгебраическое выражение;
Находить значение этого выражения при заданных значениях переменной;
Записывать неравенства, используя знаки < ≤, ≥, > и числовые промежутки, соответствующие этим неравенствам.
Записывать двойное неравенство;
Применять свойства действий над числами при нахождении значений выражений;
Решать линейное уравнение с одной переменной, применяя алгоритм его решения, и уравнения к нему сводящиеся;
Решать текстовые задачи с помощью уравнений, выделяя три этапа математического моделирования.
Типовые задачи:
1. Найдите значение числового выражения:
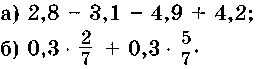
2. Решите уравнение: а)2х + 3 = 0;
б) 6х - 7 = 15 + 2х.
3. Дан открытый луч с началом в точке (-9).
Запишите обозначение, аналитическую и геометрическую модели данного числового промежутка. Сколько целых отрицательных чисел принадлежит этому промежутку?
4. Данное предложение запишите в виде числового выражения и найдите его значение:
сумма числа 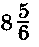 и частного чисел и частного чисел 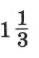 и 3,2. и 3,2.
5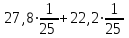 . Вычислите наиболее рациональным способом: . Вычислите наиболее рациональным способом:
|
Ученик должен уметь:
Составлять алгебраические выражения для решения задачи;
Выяснять при каких значениях переменной выражение имеет смысл;
Решать более сложные уравнения, сводящиеся к линейным;
Решать более сложные задачи с помощью уравнения, выделяя три этапа математического моделирования.;
Задачи продвинутого уровня:
1. Выясните, равна дробь нулю или она не имеет смысла:
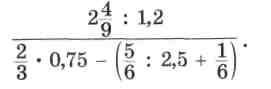
2. Упростите алгебраическое выражение и найдите его значение:
4(4с - 3) - (10с + 8) при с = 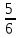 |. |.
3. Решите задачу, выделяя три этапа математического моделирования.
В книге 140 страниц. В пятницу Знайка прочитал в 1,2 раза меньше страниц, чем в субботу, и на 20 страниц больше, чем в воскресенье. Сколько страниц прочитал Знайка в субботу?
|
1. Действия с десятичными и обыкновенными дробями, смешанными числами.
2. Действия с положительными и отрицательными числами.
3. Порядок выполнения действий.
4. Решение уравнений и задач с помощью уравнений.
5. Решение пропорций.
6. Координатная прямая.
7. Двойное неравенство.
|
|
2.
|
14
|
Линейная функция
|
Ученик должен знать:
термины: прямоугольная система координат на плоскости (декартова система координат); координатная плоскость, координатные углы, начало координат; абсцисса, ордината, ось абсцисс, ось ординат;
понятия: линейное уравнение с двумя переменными (ах + by + с = 0); решение линейного уравнения с двумя переменными; независимая переменная (аргумент); зависимая переменная; линейная функция (у = kx+ т); угловой коэффициент (для линейной функции у = kx + т).
обозначения: хОу (для прямоугольной системы координат на плоскости); М(х; у) (для обозначения координат точки М на координатной плоскости); Унаиб.> Унаим. (для наибольшего и наименьшего значений линейной функции на заданном числовом промежутке).
математическую модель:у = kx; у = kx + т; ах + by+ с = 0;
Что является графиком уравнения х = а, функций у = b, у = kx, y = kx + m .
алгоритмы: алгоритм отыскания координат точки М, заданной в прямоугольной системе координат хОу; алгоритм построения точки М(а; Ь) в прямоугольной системе координат хОу;
алгоритм построения графика линейного уравнения ах + by + с = 0.
Ученик должен уметь:
Находить значение функции по заданному значению аргумента и наоборот с помощью формулы и по графику;
Задавать формулой зависимость;
Составлять таблицу значений;
«Читать» график;
Находить координаты точек пересечения графика функции с осями координат;
Строить графики линейной функции и линейного уравнения ах + by + с = 0.
Выяснять принадлежность точки графику функции.
Типовые задачи:
1. Какие из пар чисел (-1; 3), (-3; 0), (0; 4) являются решением уравнения 4х - Зу + 12 = 0?
2. Постройте график уравнения х + у - 3 = 0.
3. Преобразуйте линейное уравнение с двумя переменными -4х + 2у = 6 к виду линейной функции у= кх + т. Постройте график полученной линейной функции. По графику определите:
а) координаты точек пересечения графика с осями координат;
б) значения функции при х = -2; -1; 2;
в) значения аргумента, если у = -3; 1; 4.
4. Постройте график линейной функции у = -2х +1. С помощью графика найдите:
а) наименьшее и наибольшее значения функции на отрезке [-1; 2];
б) значения переменной х, при которых график функции расположен ниже оси Ох.
5. Найдите координаты точки пересечения прямых у = 3 - х и y= 2х.
6.Найдите координаты точек пересечения графика линейного уравнения -Зх + 2у - 6 = 0 с осями координат. Определите, принадлежит ли графику данного уравнения точка К(0,5; 3,5).
|
Ученик должен знать:
понятие углового коэффициента прямой;
свойство угловых коэффициентов прямых, являющихся графиками двух линейных функций.
Ученик должен уметь:
Находить значение функции, заданной несколькими формулами;
По формулам выяснять взаимное расположение графиков линейных функций;
Определять расположение графика линейной функции в зависимости от коэффициентов;
Находить координаты точек пересечения графиков линейных функций;
Решать несложные задачи, приводящие к понятию линейного уравнения с двумя переменными.
Задачи продвинутого уровня:
1. Найдите значение коэффициента а в уравнении ах + 2у - 30 = 0, если известно, что пара чисел (9; -3) является решением уравнения.
2. Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен прямой -Зх + у - 4 = 0. Определите, возрастает или убывает заданная вами линейная функция.
3. При каком значении р решением уравнения 5х + ру - Зр = 0 является пара чисел (1; 1)?
|
1. Координатная плоскость.
2. Решение уравнений с одной переменной.
3. Действия с положительными и отрицательными числами.
1. Действия с десятичными и обыкновенными дробями, смешанными числами.
|
|
3.
|
15
|
Системы двух линейных уравнений с двумя переменными
|
Ученик должен знать:
понятия: система двух линейных уравнений с двумя переменными; решение системы уравнений; несовместная система, неопределенная система уравнений;
математическую модель - система двух линейных уравнений с двумя переменными;
три метода решения систем линейных уравнений: графический метод, метод подстановки, метод алгебраического сложения.
Ученик должен уметь:
Выражать одну переменную уравнения через другую;
Находить значение ординаты графика функции по значению аргумента;
Решать системы линейных уравнений: графический метод, метод подстановки, метод алгебраического сложения;
Решать несложные текстовые задачи, выделяя три этапа математического моделирования с помощью системы линейных уравнений.
Типовые задачи:
1. Решить систему уравнений графический метод 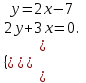
2. Решить систему уравнений методом подстановки 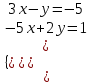
3. Решить систему уравнений методом алгебраического сложения 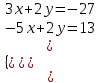
4. Решите задачу, используя для составления математической переменной две переменные:
Два числа в сумме дают 77. Найдите эти числа, если 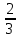 одного числа составляют 0,8 другого. одного числа составляют 0,8 другого.
|
Ученик должен уметь:
Составлять линейные уравнения с двумя переменными;
Составлять систему линейных уравнений, решение которой известно;
Решать более сложные системы уравнений с двумя переменными;
Решать более сложные задачи составлением системы уравнений с двумя переменными.
Задачи продвинутого уровня:
1. Решите задачу, выделяя три этапа математического моделирования. Периметр прямоугольника равен 48 см. Если одну его сторону увеличить в 2 раза, а другую уменьшить на 6 см, то периметр нового прямоугольника будет равен 64 см. Найдите стороны данного прямоугольника.
2. Составьте уравнение прямой, проходящей через данные точки: А(5;0); В(0;2).
3. Решите систему уравнений:
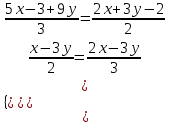
4. При каком значении р график уравнения у + рх = 0 пройдет через точку пересечения прямых у =-3/8х+15 и у= 5/6х + 73?
|
1. Решение уравнений, сводящихся к линейному.
2. Нахождение дроби, процента от числа и числа по его значению дроби (процента)
|
|
4.
|
9
|
Степень с натуральным показателем и его свойства
|
Ученик должен знать:
определение степени числа а с натуральным показателем, большим 1;
определение степени с нулевым показателем;
правила умножения и деления степеней с одинаковыми основаниями;
свойства возведения в степень произведения и степени;
Ученик должен уметь:
записывать произведение в виде степени;
находить значение степени с натуральным показателем;
применять свойства степеней с одинаковыми основаниями при нахождении значений выражений, упрощении выражений;
Типовые задачи:
1. Запишите произведение в виде степени, назовите основание
и показатель степени:
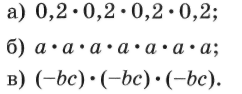
Вычислите:
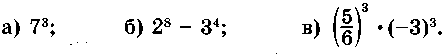
Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1.
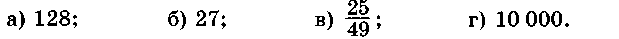
4.Решите уравнение:

5. Ребро куба равно 6 см. Найдите объем куба и площадь его поверхности.
6. Представьте выражение в виде степени:
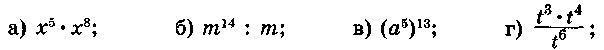

|
Ученик должен уметь:
применять свойства степеней с одинаковыми знаменателями при нахождении значений выражений, упрощении выражений, решении простейших степенных, показательных уравнений.
Задачи продвинутого уровня:
1. Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1.
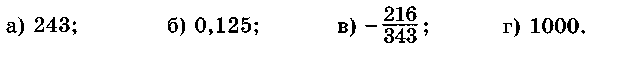
2. Решите уравнение:

3. Объем куба равен 27 см3. Найдите ребро куба и площадь его поверхности.
4. Возведите данное выражение в степень:
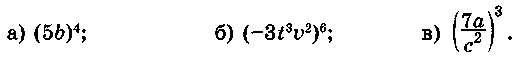
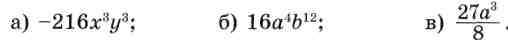
5. Вычислите
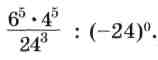 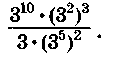
|
1. Квадрат и куб числа.
2. Действия с положительными и отрицательными числами.
3. Действия с десятичными и обыкновенными дробями, смешанными числами.
Нахождение значения числового, алгебраического выражения.
|
| |
|
|
 Скачать 416.21 Kb.
Скачать 416.21 Kb.