Рабочая программа по алгебре 7 класс. Рабочая программа по алгебре 7 класс Г. Магнитогорск, 2013 пояснительная записка

• Название: Рабочая программа по алгебре 7 класс Г. Магнитогорск, 2013 пояснительная записка
• Дата: 04.12.2022
• Размер: 416.21 Kb.
• Имя файла: Рабочая программа по алгебре 7 класс.docx
• Тип: Рабочая программа; #826872
• страница: 5 из 6

5.

8

Одночлены. Арифметические операции над одночленами

Ученик должен знать:

• 
  понятия: одночлена, коэффициента одночлена; подобных одночленов;
  
• 
  действия над одночленами;
  

Ученик должен уметь:

• 
  Записывать одночлен в стандартном виде.
  
• 
  Складывать (вычитать) подобные одночлены.
  
• 
  Представлять одночлен в виде суммы подобных од­ночленов.
  
• 
  Возводить одночлен в натуральную степень.
  
• 
  Делить одночлен на другой одночлен.
  

Типовые задачи:

1.Приведите одночлен к стандартному виду и выпишите коэффициент одночлена:



2.Выполните действия с подобными одночленами:


3. Упростите выражение и найдите его значение:


4. Решите задачу, выделяя три этапа математического моде­лирования.

Магазин увеличил розничную цену на товар по сравнению с оптовой на 20%, затем в связи с рекламной акцией снизил ее на 10%. Вычислите оптовую цену товара, если разница между оптовой и рекламной ценой составила 10 р. 80 коп.
5. Упростите выражение: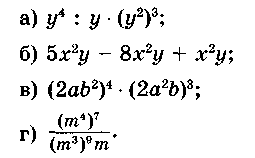



6. Вычислите:


7. Сравните значения выражений

Ученик должен уметь:

• 
  Выполнять упрощение более сложных выражений, содержащих одночлены;
  
• 
  Решать уравнения по теме.
  

Задачи продвинутого уровня:

1. Решите уравнение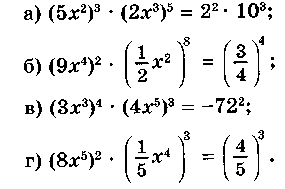




2. Упростите выражение

1. 
   Действия со степенями.
   

6.

18

Многочлены. Арифметические операции над многочленами.

Ученик должен знать:

• 
  понятия: многочлен, в частности двучлен, трехчлен; приведение подобных членов многочлена, взаимное уничтожение членов многочлена; стандартный вид многочлена; алгебраическая сумма многочленов.
  
• 
  правила: составления алгебраической суммы много­членов; умножения многочлена на одночлен; умножения многочлена на многочлен; деления многочлена на одночлен.
  
• 
  формулы:
  

(а + b)² = а² + 2аb + b² (квадрат суммы);

(а - b)² = а²- 2аb + b² (квадрат разности);

(а + b) (а - b) = а² - b² (разность квадратов);

(а - b) (a² + ab + b²) = а³-b³(разность кубов);

(а + b) (a² -ab + b²) = а³ + b³(сумма кубов).
Ученик должен уметь:

• 
  Называть члены многочлена.
  
• 
  Приводить подобные члены многочленов
  
• 
  Складывать и вычитать многочлены
  
• 
  Умножать одночлен на многочлен
  
• 
  Умножать многочлен на многочлен
  
• 
  Возводить в квадрат суммы и разности двух выражений;
  
• 
  Находить разность квадратов, сумму и разность кубов.
  

Типовые задачи:

1. Приведите многочлен к стандартному виду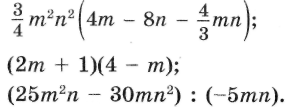




2. Приведите многочлен к стандартному виду и запишите его в порядке убывания степеней переменной:

3. Приведите многочлен

к стандартному виду и найдите его значение при р = -2, q = -1.

4. Найдите _если

5 . Решите уравнение



6. Решите задачу, выделяя три этапа математического моде­лирования.

Из пункта А в пункт В вышел пешеход. Через 1,5 ч навстре­чу ему из пункта В выехал велосипедист, скорость которо­го на 8 км/ч больше скорости пешехода. Через 2 ч после выезда велосипедиста они встретились. С какой скоростью двигался велосипедист, если расстояние от А до В равно 38 км?
7. Периметр прямоугольника 280 м. Если длину прямоуголь­ника уменьшить на 30 м, а ширину увеличить на 20 м, то его площадь уменьшится на 300 м². Найти длину и ширину данного прямоугольника.

8. Упростите выражения:



9 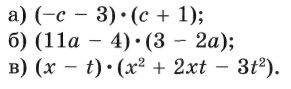. Выполните действия:


10. Раскройте скобки: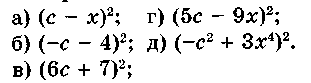


11. Замените пропуски, отмеченные символом * так, чтобы вы­полнялось равенство
12. Составьте многочлен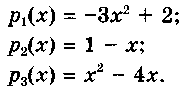

и запи­шите его в стандартном виде, если:

Ученик должен знать:

• 
  Куб суммы, куб разности двух выражений;
  

Ученик должен уметь:

• 
  Находить значение многочлена.
  
• 
  Составлять многочлены разной степени,
  
• 
  Приводить многочлен к стандартному виду.
  
• 
  Располагать многочлен по убывающим или возрастающим степеням.
  
• 
  Преобразовывать произведение в многочлен.
  
• 
  Возводить в квадрат сумму и разность сложных многочленов.
  
• 
  Представлять выражение в виде квадрата двучлена.
  

Задачи продвинутого уровня:

1. Приведите многочлен к стандартному виду и запишите его
в порядке убывания степеней переменной:


2. Используя формулы сокращенного умножения для (а + b)² и (а - b)², вычислите


_3. Упростите выражение, используя формулы сокращенного умножения:

4. Докажите, что значение выражения



не зависит от значения переменной.

7.

21

Разложение многочленов на множители

Ученик должен знать:

• 
  понятия матема­тического языка: разложение многочлена на множители; алгебраическая дробь, сокращение алгебраической дроби; тождество, тождественно равные выражения, тожде­ственное преобразование выражения.
  

Ученик должен уметь:

• 
  пользоваться приемами разло­жения многочлена на множители: вынесение общего множителя за скобки; группировка; использование формул сокращенного умножения; выделение полного квадрата.
  

Типовые задачи:

1. Разложите на множители: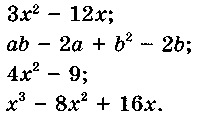



2.Сократите дробь:

а) б)
3. Решите уравнение х³- 64х = 0.

Ученик должен уметь:

раскладывать многочлены на множители с помощью комбинаций различных приемов.
Задачи продвинутого уровня:

1. Докажите тождество

х² - 12х + 32 = (х - 8)(х - 4).

2. Вычислите наиболее рациональным способом:


3. Разложите на множители




4. Решите уравнение


5. Разложите многочлен на множители,

выделив полный квадрат двучлена.

8.

11

Функция у=х².

Ученик должен знать:

• 
  термины: парабола, ось (ось симметрии) параболы, ветви параболы, вершина параболы; непрерывная функция, разрыв функции; кусочная функция; область определения функции; чтение графика.
  
• 
  математическую моде­ль: у = х² , y = f(x).
  
• 
  график функции у = х².
  

Ученик должен уметь:

• 
  строить и «читать» график функции у = х²;
  
• 
  использовать алгоритм графического решения урав­нения вида f(x) = g(x).
  

Типовые задачи:

1. Постройте график функции у= х².
С помощью графика найдите:

а) значения функции при значении аргумента, равном -2; 1; 3;

б) значения аргумента, если значение функции равно 4;

в) наибольшее и наименьшее значения функции на от­резке [-3; 0].
2. Решите графически уравнение -х²= 2х - 3.
3. Дана функция где

<

а) Вычислите:

б) Укажите область определения функции у = f(х).

Ученик должен уметь:

• 
  строить графики кусочных функций.
  

Задачи продвинутого уровня:

1. Дана функция где При каких значениях аргумента верно равенство
2. Постройте график функции

1. Линейная функция, её график.
2. Свойства функции:

а) точки пересечения с осями координат;

б) наибольшее и наименьшее значения функции;

в) возрастающая, убывающая функция.

9.

0

Элементы комбинаторики, статистики и теории вероятностей

Ученик должен знать:

• 
  правило умножения и дерево вариантов,
  
• 
  n! .
  

Ученик должен уметь:

• 
  Решать простейшие комбинаторные задачи, используя правило умножения.
  
• 
  Строить дерево вариантов.
  
• 
  Вычислять n!
  
• 
  Решать несложные комбинаторные задачи, используя выбор нескольких элементов.
  
• 
  Решать несложные комбинаторные задачи, используя сочетания.