Рабочая программа по алгебре 7 класс. Рабочая программа по алгебре 7 класс Г. Магнитогорск, 2013 пояснительная записка
 Скачать 416.21 Kb. Скачать 416.21 Kb.
|
Тематика контрольных работ по алгебре
Материально-техническое обеспечение учебного предмета «Алгебра» Материально-техническое обеспечение преподавания учебного предмета «Математика» ориентировано на реализацию федерального компонента Государственного образовательного стандарта по математике и соответствует требованиям к оснащению образовательного процесса, изложенным в письме МОиН РФ от 01 апреля 2005 г. № 03-417 «О перечне учебного и компьютерного оборудования для оснащения образовательных учреждений». Для преподавания учебной дисциплины «Алгебра» используется: Единая коллекция цифровых образовательных ресурсов: http://school-collection.edu.ru/. Веб-сайты, перечень которых представлен в таблице:
Особенности курса «Алгебра» с учетом выбранного УМК Основные цели и задачи математического образования в школе, которые реализованы в выбранном учебно-методическом комплексе, заключаются в следующем: содействовать формированию культурного человека, умеющего мыслить, понимающего идеологию математического моделирования реальных процессов, владеющего математическим языком не как языком общения, а как языком, организующим деятельность, умеющего самостоятельно добывать информацию и пользоваться ею на практике, владеющего литературной речью и умеющего в случае необходимости построить ее по законам математической речи. Исходные положения теоретической концепции курса алгебры для 7—11 классов по авторской программе А.Г.Мордковича можно сформулировать в виде двух лозунгов. Математика в школе — не наука и даже не основа наук, а учебный предмет. Основной задачей учителя должно стать развитие учащихся, поэтому следует продумать выбор места и времени (стратегия) и этапы постепенного подхода к формальному определению на основе предварительного изучения понятия на более простых уровнях (тактика). Таковых уровней в математике можно назвать три: наглядно-интуитивный, когда новое понятие вводится с опорой на интуитивные или образные представления учащихся; рабочий (описательный), когда от учащегося требуется уметь отвечать не на вопрос «что такое?», а на вопрос «как ты понимаешь? »; формальный. Стратегия введения определений сложных математических понятий в выбранном УМК базируется на положении о том, что выходить на формальный уровень следует при выполнении двух условий: 1) если у учащихся накопился достаточный опыт для адекватного восприятия вводимого понятия, причем опыт по двум направлениям — вербальный (опыт полноценного понимания всех слов, содержащихся в определении) и генетический (опыт использования понятия на наглядно-интуитивном и рабочем уровнях); 2) если у учащихся появилась потребность в формальном определении понятия. То или иное понятие математики практически всегда проходило в своем становлении три указанные выше стадии (наглядное представление, рабочий уровень восприятия, формальное определение), причем переход с уровня на уровень зачастую был весьма длительным по времени и болезненным. Не учитывать этого нельзя. Надо дать учащимся время пережить это, не спеша переходить с уровня на уровень. Поэтому, в частности, существенной ошибкой является традиция предлагать определение функции не подготовленным для этого учащимся 7 класса. В авторской программе А.Г. Мордковича это понятие «созревает» с 7 по 9 класс. Поначалу, пока изучаются простейшие функции (линейная, обратная пропорциональность, квадратичная и т. д. — это материал 7—8 классов), следует отказаться от формального определения функции и ограничиться описанием, не требующим заучивания. Ничего страшного в этом нет, о чем свидетельствует и история математики. Многие математические теории строились, развивались, обогащались все новыми и новыми фактами и приложениями, несмотря на отсутствие определения основного понятия этой теории. Можно строить теорию, даже достаточно строгую, и при отсутствии строгого определения исходного понятия — во многих случаях это оправдано с методической точки зрения. Итак, в отличие от сложившихся традиций в 7 классе не вводится определение функции, хотя работаем с функциями и в 7, и в 8 классе очень много. И только в 9 классе, проанализировав накопленный учащимися опыт в использовании понятия функции и в работе со свойствами функции в курсе алгебры 7 и 8 классов, учащиеся убеждаются в том, что у них появилась и потребность в формальном определении понятия функции и ее свойств. Что касается свойств функций, то следует подчеркнуть, что фактически в 7 классе работаем с учащимися на наглядно-интуитивном уровне, в 8 классе — на рабочем уровне и только в классе выходим на формальный уровень. Новый математический термин и новое обозначение должны появляться мотивированно, только тогда, когда в них возникает необходимость (в первую очередь в связи с появлением новой математической модели). Немотивированное введение нового термина провоцирует запоминание (компонент обучения) без понимания (и, следовательно, без развития). Математика в школе — гуманитарный учебный предмет. Математика — гуманитарный (общекультурный) предмет, который позволяет субъекту правильно ориентироваться в окружающей действительности и «ум в порядок приводит». Математика — наука о математических моделях. Модели описываются в математике специфическим языком (термины, обозначения, символы, графики, графы, алгоритмы и т. д.). Значит, надо изучать математический язык, чтобы мы могли работать с любыми математическими моделями. Особенно важно при этом подчеркнуть, что основное назначение математического языка — способствовать организации деятельности (тогда как основное назначение обыденного языка — служить средством общения), а это в наше время очень важно для культурного человека. Поэтому в авторской программе А.Г.Мордковича математический язык и математическая модель — ключевые слова в постепенном развертывании курса, его идейный стержень. При наличии идейного стержня математика предстает перед учащимися не как набор разрозненных фактов, которые учитель излагает только потому, что они есть в программе, а как цельная развивающаяся и в то же время развивающая дисциплина общекультурного характера. В наше время владение хотя бы азами математического языка — непременный атрибут культурного человека. Гуманитарный потенциал школьного курса алгебры заключается в следующем: во-первых, в том, что владение математическим языком и математическим моделированием позволит учащемуся лучше ориентироваться в природе и обществе; во-вторых, в том, что математика по своей внутренней природе имеет богатые возможности для воспитания мышления и характера учащихся; в-третьих, в реализации в процессе преподавания идей развивающего и проблемного обучения; в-четвертых, в том, что уроки математики (при правильной постановке) способствуют развитию речи обучаемого в не меньшей степени, чем уроки русского языка и литературы. Из основных содержательно-методических линий школьного курса алгебры приоритетной в авторской программе А.Г.Мордковича является функционально-графическая линия. Это выражается прежде всего в том, что, какой бы класс функций, уравнений, выражений ни изучался, построение материала практически всегда осуществляется по жесткой схеме: функция — уравнения — преобразования. Для понимания учащимися курса алгебры в целом важно прежде всего, чтобы они полноценно усвоили первичные модели (функции). Это значит, что нужно организовать их деятельность по изучению той или иной функции так, чтобы рассмотреть новый объект (конкретную математическую модель — функцию) системно, с разных сторон, в разных ситуациях. В то же время не следует рассматривать набор случайных сюжетов, различных для разных классов функций — это создаст ситуацию дискомфорта в обучении. Возникает методическая проблема выделения в системе упражнений по изучению того или иного класса функций инвариантного ядра, универсального для любого класса функций. Инвариантное ядро в учебниках и задачниках А.Г. Мордковича состоит из шести направлений: графического решения уравнений; отыскания наибольшего и наименьшего значений функции на заданном промежутке; преобразования графиков; функциональной символики; кусочных функций; чтения графика. Графический (или, точнее, функционально-графический) метод решения уравнений первым и одним из главных при решении уравнений любых типов. Неудобства, связанные с применением графического метода, как правило, и создают ту проблемную ситуацию, которая приводит к необходимости отыскания алгоритмов аналитических способов решения уравнения. Что дает этот метод для изучения той или иной функции? Он приводит ученика к ситуации, когда график функции строится не ради графика, а для решения другой задачи — для решения уравнения. График функции является не целью, а средством, помогающим решить уравнение. Это способствует и непосредственному изучению функции, и ликвидации того неприязненного отношения к функциям и графикам, которое, к сожалению, характерно для традиционных способов организации изучения курса алгебры в общеобразовательной школе. В учебных пособиях А.Г. Мордковича графический способ решения уравнения всегда предшествует аналитическим способам. Ученики вынуждены применять его, привыкать к нему и относиться к нему, как к своему первому помощнику (они как бы «обречены на дружбу» с графическим методом), поскольку никаких других приемов решения того или иного уравнения они к этому времени не знают. Для правильного формирования у учащихся как самого понятия функции, так и представления о методологической сущности этого понятия очень полезны кусочные функции. Во многих случаях именно кусочные функции являются математическими моделями реальных ситуаций. Использование таких функций способствует преодолению обычного заблуждения многих учащихся, отождествляющих функцию только с ее аналитическим заданием в виде некоторой формулы, готовит как в пропедевтическом, так и в мотивационном плане и определение функции, и понятие непрерывности. Использование на уроках кусочных функций дает возможность учителю сделать систему упражнений более разнообразной (что важно для поддержания интереса к предмету у обучаемых), творческой (можно предложить учащимся сконструировать примеры самим). Отметим и воспитательный момент: это воспитание умения принять решение, зависящее от правильной ориентировки в условиях, это и своеобразная эстетика — оценка красоты графиков кусочных функций, предложенных разными учениками. Распределение содержания обучения по классам 7 класс 1. Математический язык. Математическая модель. Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней. 2. Линейная функция. Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М (а; Ь) в прямоугольной системе координат. Линейное уравнение с двумя переменными. Решение уравнения ах + Ьу + с = 0. График уравнения. Алгоритм построения графика уравнения ах + Ьу + с = 0. Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Линейная функция у = кх и ее график. Взаимное расположение графиков линейных функций. 3. Системы двух линейных уравнений с двумя переменными. Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи). 4. Степень с натуральным показателем. Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем. 5. Одночлены. Операции над одночленами. Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен. 6. Многочлены. Арифметические операции над многочленами. Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов. Деление многочлена на одночлен. 7. Разложение многочленов на множители. Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата. Понятие алгебраической дроби. Сокращение алгебраической дроби. Тождество. Тождественно равные выражения. Тождественные преобразования. 8. Функция у = х2. Функция у = х2, ее свойства и график. Функция у = -х2, ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Разъяснение смысла записи у = f(х). Функциональная символика. 9. Элементы логики, комбинаторики. Множество. Элемент множества, подмножества. Объединение и пересечение множеств. Комбинаторные задачи. Простейшие комбинаторные задачи. Правило умножения и дерево вариантов. Перестановки. n!. Выбор нескольких элементов. Сочетания. 10. Обобщающее повторение. Особенности планирования учебного материала по алгебре в 7 - 9 классах Согласно 2 варианту тематического планирования учебного материала на изучение алгебры в 7, 8, 9 классах отводится 136 часов в течение учебного года. Календарное и тематическое планирования по алгебре в 7, 8, 9 классах составлены из расчета 4 часа в неделю. В Примерной программе основного общего образования по математике (Сайт МОиН РФ, 2005 г.) на изучение темы «Элементы логики, комбинаторики, статистики и теории вероятностей» отводится 45ч на 5 лет обучения (5-9 классы), что в среднем составляет 9 часов в год. В авторской программе А.Г.Мордковича Программы. Алгебра 7-9 классы/авт.-сост. И.И.Зубарева, А.Г.Мордкович.-2 изд., испр. и доп. – М.: Мнемозина, 2009 г. на изучение этой темы отводится в 9-м классе 12 часов. В связи с этим в рабочей программе изменено количество часов в некоторых темах курса алгебры в 7, 8 классах и добавлены часы на изучение комбинаторики, статистики и теории вероятностей в объеме 15 часов за два года обучения. Всего на изучение темы «Элементы логики, комбинаторики, статистики, теории вероятностей» предусмотрено в 7-9 классах 27 часов. После изучения основных блоков предусматривается проведение контрольных работ. В ходе изучения блока для учащихся предусмотрена домашняя контрольная работа, которая сдается учащимися после изучения соответствующего блока перед контрольной работой. Планирование учебного материала по алгебре Класс 7 2 вариант: 4 ч. в неделю, всего 136 ч. в год.
|

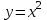 »
»