Главная страница
Навигация по странице:

  • Задача 2. Пример 1.

    		•

    кр. Рабочая программа по курсу эконометрика


    Скачать 0.71 Mb.
    НазваниеРабочая программа по курсу эконометрика
    Дата07.05.2021
    Размер0.71 Mb.
    Формат файлаdoc
    Имя файлаkr_ekonometrika.doc
    ТипРабочая программа
    #202405
    страница5 из 6
    1   2   3   4   5   6

    Задача 25

    Имеются данные по семи банкам страны о размере прибыли ( ) и объёмах выданных кредитов

    № наблюдения
    1
    2
    3
    4
    5
    6
    7

    Кредиты,

    200
    300
    200
    220
    100
    250
    250

    Прибыль,

    19
    30
    26
    22
    13
    35
    28


    Задача 26

    Изучается зависимость доходности акций предприятия ( ) от темпа роста валового внутреннего продукта . Полученные данные отражены в таблице:

    Год
    1
    2
    3
    4
    5
    6
    7

    Темп роста валового

    Внутреннего продукта, %
    5,6
    6,3
    7,8
    7,1
    4,9
    5,4
    6,8

    Доходность акций

    предприятияБ %
    14,2
    18,9
    23,2
    17,9
    8,8
    15,4
    19,4


    Задача 27

    Для семи предприятий области анализируется зарплата в зависимости от количества сотрудников . Данные по предприятиям приведены в таблице:

    № предпр.
    1
    2
    3
    4
    5
    6
    7

    Кол-во сотрудн., чел
    100
    150
    200
    250
    300
    350
    400

    Зарплата, тыс. тыс. руб.
    20
    24
    27
    30
    32
    37
    41



    Задача 28

    По семи регионам приводятся следующие данные:

    № региона
    1
    2
    3
    4
    5
    6
    7

    Среднедушевой прожиточный минимум в день одного трудоспособного, у.е.., x
    78
    82
    87
    79
    89
    106
    67

    Среднедневная заработная плата, у.е., y
    133
    148
    134
    154
    162
    195
    139


    Задача 29

    По семи регионам приводятся следующие данные:

    № региона
    1
    2
    3
    4
    5
    6
    7

    Среднедушевой прожиточный минимум в день одного трудоспособного, у.е.., x
    81
    77
    85
    79
    93
    100
    72

    Среднедневная заработная плата, у.е., y
    124
    131
    146
    139
    143
    159
    135


    Задача 30

    По семи регионам приводятся следующие данные:

    № региона
    1
    2
    3
    4
    5
    6
    7

    Среднедушевой прожиточный минимум в день одного трудоспособного, у.е.., x
    74
    81
    90
    79
    89
    87
    77

    Среднедневная заработная плата, у.е., y
    122
    134
    136
    125
    120
    127
    125


    Задача 2.

    Пример 1. В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны . В этом случае хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

    Рассмотрим эконометрическую модель экономики страны:



    где y1 – расходы на конечное потребление данного года; y2 – валовые инвестиции в текущем году; y3 – расходы на заработную плату в текущем году; y4 – валовой доход за текущий год; x1 -- валовой доход предыдущего года; x2 – государственные расходы текущего года; а - свободный член уравнения, -- случайные ошибки.

    Решение. В этой модели четыре эндогенные переменные (y1, y2, y3, y4). Переменная y4 задана тождеством. Поэтому практически статистическое решение необходимо только для первых трех уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределенных переменных - экзогенную x2 и лаговую x1.

    При практическом решении задачи на основе статистической информации за ряд лет или по совокупности регионов за один год в уравнениях для эндогенных переменных y1, y2, y3 обычно содержится свободный член (a1, a2, a3), значение которого аккумулирует влияние неучтенных в уравнении факторов и не влияет на определение идентифицируемости модели.

    Поскольку фактические данные об эндогенных переменных y1, y2, y3 могут отличаться от теоретических постулируемых моделью, то принято в модель включать случайную составляющую для каждого уравнения системы, исключив тождества. Случайные составляющие обозначены через . Они не влияют на решение вопроса об идентификации модели.

    П е р в о е у р а в н е н и е.

    Н: эндогенных переменных три ( ) - = 3, предопределенных переменных нет - = 0.

    Выполняется необходимое равенство: M - m1 = 2 - 0 = 2 = k1 - 1 = 3 - 1 =2, следовательно , уравнение идентифицируемо.

    Д: в первом уравнении отсутствуют y2, x1, x2. Построим матрицу из коэффициентов при них в других уравнениях системы:

    Уравнение Отсутствующие переменные

    y2 x1 x2

    Второе -1 0

    Третье 0 0

    Четвертое 1 0 1



    Определитель матрицы не равен нулю, ранг матрицы равен 3; следовательно выполняется достаточное условие идентификации (r(A) = 3 = K - 1 = 4 - 1 = 3), и первое уравнение идентифицируемо.

    В т о р о е у р а в н е н и е.

    Н: эндогенных переменных две (y2, y3) - k2 = 2; предопределенных переменных одна (x1) - m2 = 1.

    Выполняется необходимое равенство: M - m2 = 2 - 1 = 1 = k2 - 1 = 2 - 1 = 1, следовательно, уравнение идентифицируемо.

    Д: во втором уравнении отсутствуют y1, y4 x2. Построим матрицу коэффициентов при них в других уравнениях системы:

    Уравнение Отсутствующие переменные

    y1 y4 x2

    Первое -1 0

    Третье 0 0

    Четвертое 1 -1 1



    Определитель матрицы не равен нулю, ранг матрицы равен 3, следовательно, выполняется достаточное условие идентификации (r(A) = 3 = K - 1 = 4 - 1 = 3), и второе уравнение идентифицируемо.

    Т р е т ь е у р а в н е н и е.

    Н: эндогенных переменных две (y3, y4) - k3 =2; предопределенных переменных одна (x1) - m3 = 1.

    Выполняется необходимое равенство: M - m3 = 2 - 1 = 1 = k3 - 1 = 1, следовательно, уравнение идентифицируемо.

    Д: в третьем уравнении отсутствуют y1, y2, x2. Построим матрицу из коэффициентов при них в других уравнениях системы:

    Уравнение Отсутствующие переменные

    y1 y2 x2

    Первое -1 0 0 Второе 0 -1 0 Четвертое 1 1 1



    Определитель матрицы не равен нулю, ранг матрицы равен 3, следовательно, выполняется достаточное условие идентификации (r(A) = 3 = K - 1 = 4 - 1 = 3), и третье уравнение идентифицируемо.

    Следовательно, исследуемая система идентифицируема.

    Приведенная форма модели:



    Пример 2.

    Макроэкономическая модель: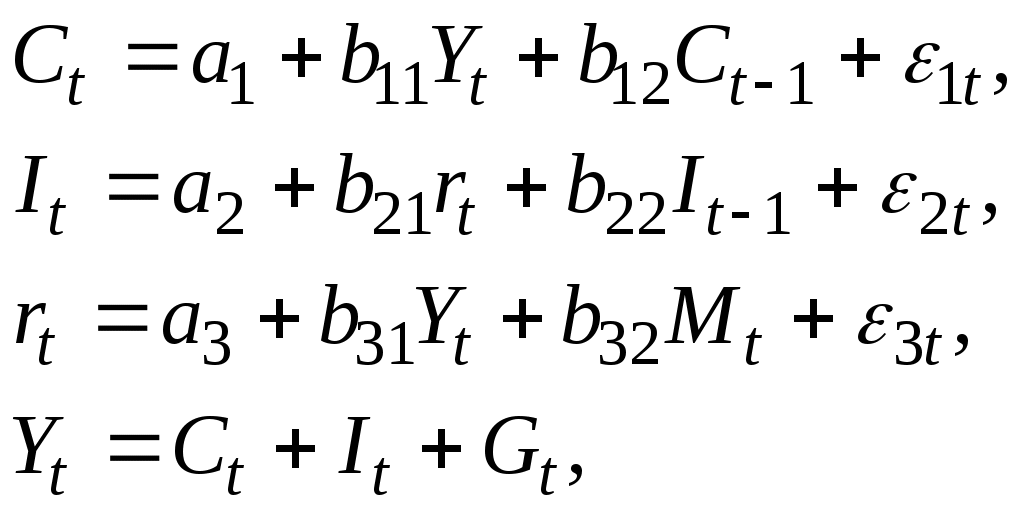



    где C—расходы на потребление, Y –совокупный доход в период t, r – процентная ставка в период t, I – инвестиции в период t, M – денежная масса в период t, G – государственные расходы в период t,It-1 - инвестиции в период t-1, Ct-1 - расходы на потребление в период t, t – текущий период, t-1 – предыдущий период.

    РЕШЕНИЕ.

    Модель включает четыре эндогенные переменные ( ) – K = 4 и четыре предопределенные переменные (две экзогенные переменные - и две лаговые эндогенные переменные - ) – M = 4.

    Проверим необходимое условие идентификации для уравнений модели.

    I уравнение.

    Это уравнение включает две эндогенные переменные ( ) – k1 = 2 и одну предопределенную переменную – m1 = 1. Таким образом, M - m1 = 4 - 1 = 3 > k1 - 1 = 2 - 1 = 1. Уравнение сверидентифицировано.

    II уравнение.

    Уравнение II включает две эндогенные переменные ( ) – k2 = 2 и одну предопределенную переменную – m2 = 1. Следовательно, M - m2 = 4 - 1 = 2 > k2 -1 = 2 - 1 = 1. Уравнение сверхидентифицировано.

    III уравнение.

    Уравнение III включает две эндогенные переменные -- k3 = 2 и одну предопределенную переменную – m3 = 1. Следовательно, M - m3 = 4 - 1 = 3 > k3 - 1 = 2 - 1 = 1. Уравнение сверхидентифицировано.

    IV уравнения.

    Четвертое уравнение представляет собой тождество, параметры которого известны. Поэтому идентифицировать это уравнение не нужно.

    Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
    Сt
    Yt
    Ct-1
    It
    rt
    It-1
    Mt
    Gt

    I уравнение
    -1
    b11
    b12
    0
    0
    0
    0
    0

    II уравнение
    0
    0
    0
    -1
    b21
    b22
    0
    0

    III уравнение
    0
    b31
    0
    0
    -1
    0
    b32
    0

    IV уравнение
    1
    -1
    0
    1
    0
    0
    0
    1

    В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т.е. 4 - 1 = 3.

    I уравнение.

    Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид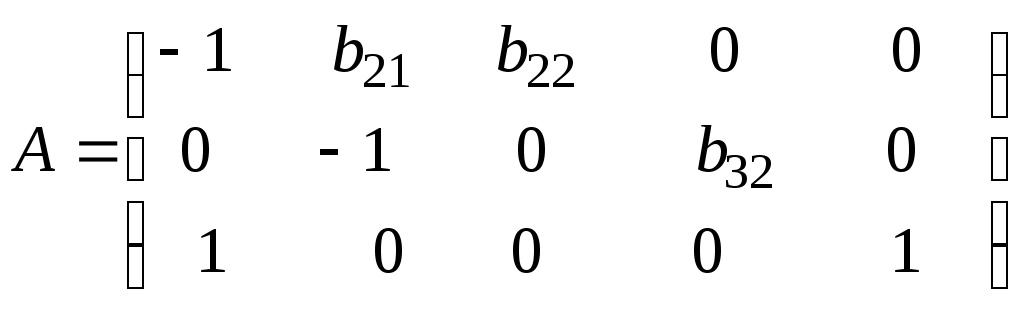



    Ее ранг равен 3, так как определитель квадратной подматрицы 3 * 3 этой матрицы не равен нулю:



    Достаточное условие идентификации для I уравнения выполняется.

    II уравнение.

    Выпишем матрицу коэффициентов при переменных, не входящих в уравнение:



    Ее ранг равен 3, так как определитель квадратной подматрицы 3 * 3 этой матрицы не равен нулю:



    Достаточное условие идентификации для II уравнения выполняется.

    Ш уравнение.

    Выпишем матрицу коэффициентов при переменных, не входящих в уравнение: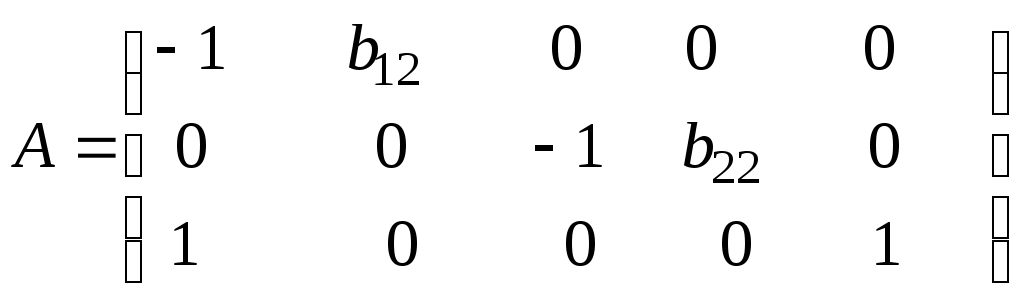



    Ее ранг равен 3, так как определитель квадратной подматрицы 3 * 3 этой матрицы не равен нулю:



    Достаточное условие идентификации для II уравнения выполняется.

    Таким образом, все уравнения модели сверхидентифицированы. Модель в целом является сверхидентифицированной.

    2. Запишем приведенную форму модели:









    где U1, U2, U3, U4 - случайные ошибки.

    1   2   3   4   5   6

    написать администратору сайта