кр. Рабочая программа по курсу эконометрика
 Скачать 0.71 Mb.
|
Тема 6. Системы эконометрических уравненийВиды систем эконометрических уравнений. Независимые системы. Рекурсивные системы. Системы одновременных (совместных) уравнений. Структурная и приведенная формы эконометрической модели. Проблемы идентификации. Косвенный и двухшаговый метод наименьших квадратов, общая схема алгоритма расчетов. Применение эконометрических моделей. Модель Кейнса (статистическая и динамическая формы). Модель Клейна (1). Литература 1. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. - М.: Дело, 1997. - с.142-163. 2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. - М.: ЮНИТИ. 1998. - с. 907-956. 3. Доугерти К. Введение в эконометрику. - М.: ИНФРА-М, 1997. - с. 322-347. 4. Эконометрика Учебное пособие /И.И. Елисеева. С.В. Курышева, Д.М. Гордиенко и др. - М.: Финансы и статистика, 2001. ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задача 1 Администрация страховой компании приняла решение о введении нового вида услуг – страхование на случай пожара. С целью определения тарифов по выборке из 10 случаев пожаров анализируется зависимость стоимости ущерба, нанесенного пожаром от расстояния до ближайшей пожарной станции (табл. 1) Табл. 1
Задание 1. Постройте поле корреляции и сформулируйте гипотезу о форме связи. 2. Рассчитайте параметры линейной регрессии. 3. Оцените тесноту связи с помощью показателей корреляции и детерминации. 4. Оцените с помощью средней квадраической ошибки и средней ошибки аппроксимации качество уравнения. 5. Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом. 6. Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. 7. Оцените статистическую значимость коэффициента регрессии и коэффициента корреляции. 8. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. 9. Оцените полученные результаты, оформите выполненное задание в виде отчета. 1. Построим поле корреляции (рис. 1). По расположению эмпирических точек можно предположить наличие линейной корреляционной зависимости между переменными 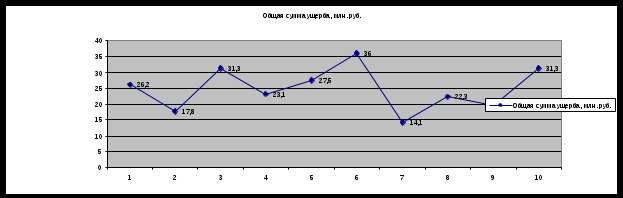 и  , т.е. можно принять гипотезу о линейной связи. Поэтому уравнение регрессии будем искать в виде линейного уравнения  Рис. 1. Поле корреляции 2. Найдем оценки параметров  и  . Все расчеты представлены в таблице
Система нормальных уравнений для нахождения оценок параметров 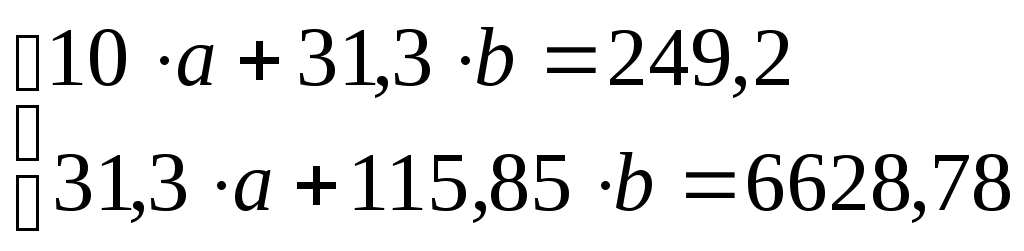и имеет вид:  Уравнение линейной регрессии  Коэффициент регрессии  говорит о том, что при увеличении расстояния до пожарной станции на 1 км общая сумма ущерба увеличивается в среднем на 4,687 млн. руб.Проверим правильность расчетов сравнением сумм  . . 3. Найдем коэффициент корреляции и коэффициент детерминации. Коэффициента корреляции:  Или  ; ;   Так как значение коэффициента больше 0,9, то это говорит о наличии весьма высокой связи между признаками. Коэффициент детерминации: 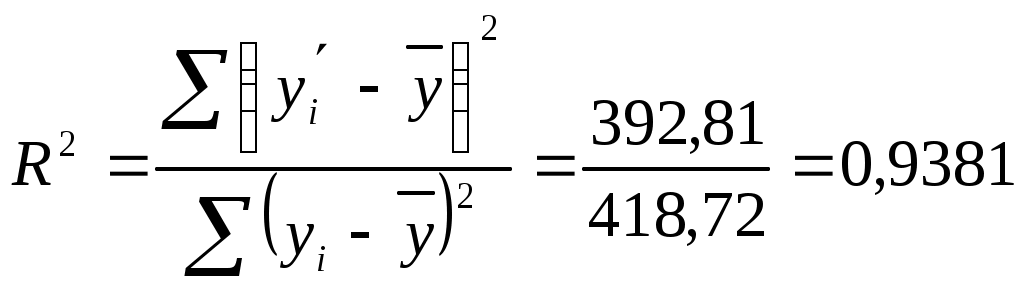 Проверка  Это означает, что 96,86% вариации общей суммы ущерба (y) объясняется вариацией фактора x – расстояния до ближайшей станции (общая сумма ущерба на 96,86% зависит от расстояния до ближайшей станции, и лишь на 3,14% зависит от факторов, не включенных в модель). 4. Найдем среднюю квадратическую ошибку и среднюю ошибку аппроксимации. Средняя квадратическая ошибка: 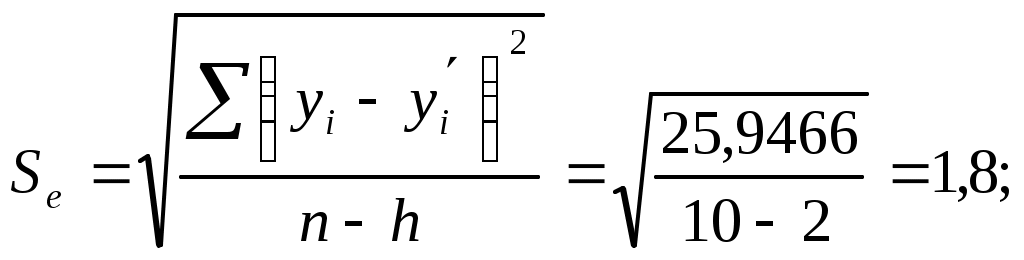 Так как  , то использование модели регрессии является целесообразным.Средняя ошибка аппроксимации 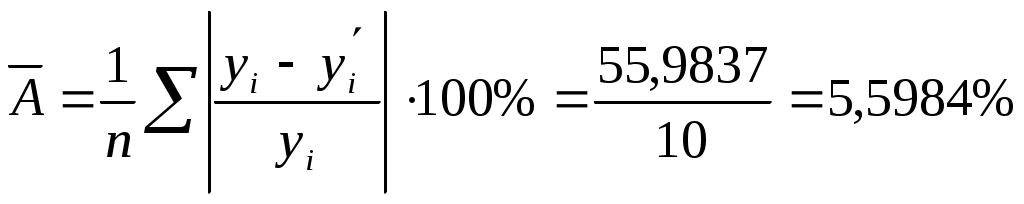 Качество построенной модели оценивается как хорошее, так как  не превышает 10%.5. Найдем коэффициент эластичности:  Коэффициент эластичности говорит о том, что при увеличении фактора x (расстояния до ближайшей станции) на 1% от уровня  , т.е. на 0,0313 км (31 м), приведет к увеличению результативного признака y (общей суммы ущерба) на 0,5887% относительно уровня  млн. руб., т.е. на 0,1467 млн. руб. (146700 руб.).6. Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера. Фактическое значение F-критерия составит:  Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы  составляет  . Так как  , то уравнение регрессии признаётся статистически значимым.7. Оценку статистической значимости коэффициента регрессии и коэффициента корреляции проведем с помощью t-статистики Стьюдента. Определим стандартные ошибки 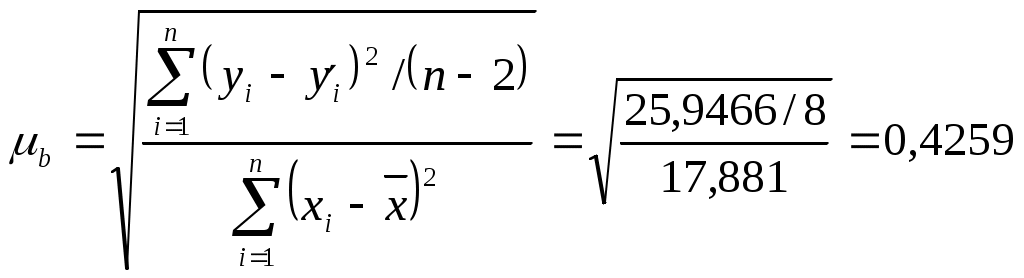 :  Тогда   Табличное значение t-критерия для числа степеней свободы  и уровня значимости  составит  .Фактические значения t-статистики превосходят табличное значение:  ,Поэтому параметры b, r не случайно отличаются от нуля, а статистически значимы. 8. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Решение.  ; .  . .ЗАДАЧИ 01 -- 30 Задание к задачам 01 – 30. 1. Постройте поле корреляции и сформулируйте гипотезу о форме связи. 2. Рассчитайте параметры линейной регрессии. 3. Оцените тесноту связи с помощью показателей корреляции и детерминации. 4. Оцените с помощью средней квадраической ошибки и средней ошибки аппроксимации качество уравнения. 5. Дайте с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом. 6. Оцените с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.  7. Оцените статистическую значимость коэффициента регрессии и коэффициента корреляции.  8. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. 9. Оцените полученные результаты, оформите выполненное задание в виде отчета. |
=3,13
=24,92
=11,585
=86,38