курсовой проект. Расчет характеристик трансформаторов и электрических двигателей з

• Название: Расчет характеристик трансформаторов и электрических двигателей з
• Анкор: курсовой проект
• Дата: 28.11.2021
• Размер: 0.78 Mb.
• Имя файла: Kursovoy_proekt_Dolzhenkov_A_A_AEb-19-1.docx
• Тип: Курсовой проект; #284091
• страница: 6 из 10

2.2 Расчет характеристик трансформатора

2.2.1 Паспортные данные

Паспортные данные трансформатора представлены в таблице 2.1.
Таблица 2.1 – Паспортные данные трансформатора типа ТДН-10000/110

Номер варианта	Тип трансформатора	Sном, кВА	U1ном, кВ	U2ном, кВ	P0, кВт	Pк, кВт	Uк, %	Iхх, %	Схема соединения и группа
6	ТДН-10000/110	10000	6,6	115	14	60	10,5	0,7	Y0/Δ-II

где S_ном - номинальная мощность трансформатора;

U_1ном - номинальное линейное напряжение первичной обмотки;

U_2ном - номинальное линейное напряжение вторичной обмотки;

P₀ - мощность потерь холостого хода;

P_к -мощность потерь короткого замыкания;

U_к - напряжение короткого замыкания в процентах относительно фазного напряжения первичной обмотки;

I_хх - ток холостого хода в процентах от номинального фазного тока первичной обмотки.

2.2.2 Электрическая схема соединения обмоток трансформатора

Электрическая схема трансформатора с соединением Y₀/Δ и группой II представлена на рисунке 2.1.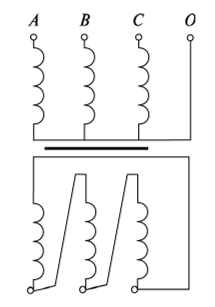



Рисунок 2.4 – Электрическая схема соединения трансформатора по схеме звезда-треугольник

2.2.3 Номинальные фазные напряжения первичной и вторичной обмоток

Фазное напряже­ние вычисляется с учетом следующих соотношений: при соедине­нии обмоток "звездой" U_л=√3U_ф, а при соединении "треугольником" U_л=U_ф.

Так как первичная обмотка имеет соединение "звездой", то фазное напряжение будет находится по формуле (2.1)


где U_1ф – фазное напряжение на первичной обмотке, В.

U_1л – линейное напряжение на первичной обмотке, В.
Подставив данные в формулу (2.1), получим

Вторичная обмотка соединена "треугольником", поэтому фазное напряжение будет равно линейному

2.2.4 Определение коэффициента трансформации

Расчетный коэффициент трансформации трехфазного транс­форматора определяется отношением фазных напряжений в режиме холостого хода, которое практически равно отношению ЭДС, так как при разомкнутой цепи вторичной обмотки U₁≈E₁, а U₂=E₂. Поэтому выражение для коэффициента трансформации можно записать как (2.2)


где n – коэффициент трансформации;

U_1ф – фазное напряжение первичной обмотки, В;

U_2ф – фазное напряжение вторичной обмотки, В.
Подставив данные в (2.2) получим

2.2.5 Номинальные линейные и фазные токи первичной и вторичной обмоток

Полная мощность S_ном, указанная в паспортных данных трансформатора, относится к первичной и вторичной обмотке, т.е. формула имеет вид (2.3)


где S_ном – номинальная полная мощность трансформатора, ВА;

U_1ном, U_2ном – соответственно линейные значения напряжений первичной и вторичной обмоток, В;

I_1ном, I_2ном – соответственно линейные значения токов первичной и вторичной обмоток, А.
Выразив ток из формулы (2.3) получим следующее выражение (2.4)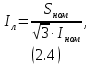

Линейный ток первичной обмотки, в соответствии с формулой (2.4), составит

Линейный ток вторичной обмотки

При вычислении фазных значений токов необходимо учитывать следующие соотношения: при соединении обмоток в "звезду" I_л=I_ф, а при соединении в "треугольник" I_л=√3I_ф.

Тогда фазный ток первичной обмотки будет равен линейному


где I_1ф – фазный ток первичной обмотки, А;

I_2л – линейный ток первичной обмотки, А.
Фазный ток вторичной обмотки вычислим по формуле (2.5)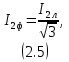


где I_2ф – фазный ток вторичной обмотки, А

I_2л – линейный ток вторичной обмотки, А.
Подставив значения в формулу (2.5), получим

2.2.6 Внешняя характеристика трансформатора при активно-индуктивной нагрузке (cosφ₂=0,8)

Уравнение электрического равновесия вторичной обмотки имеет вид (2.6)


где U₂ – напряжение на зажимах вторичной обмотки, В;

E₂ – ЭДС вторичной обмотки. В;

R₂ – активное сопротивление вторичной обмотки, Ом;

X₂ – реактивное сопротивление вторичной обмотки, Ом;

I₂ – ток вторичной обмотки, А.
Из уравнения электрического равновесия вторичной обмотки трансформатора ясно, что нап­ряжение U₂ с ростом нагрузки и, следовательно, тока I₂ уменьшается из-за увеличения активного и индуктивного падения напряжения во вторичной обмотке. При этом можно считать, что результирующий магнитный поток Ф в сердечнике и ЭДС E₂ остаются примерно постоянными независимо от режима работы. Отклонение напряжения U₂ от номинального напряжения при холостом ходе U_2ном при U₁=const характеризуется процентным изменением напряжения (2.7)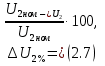


где ΔU_2% – процентное изменение вторичного напряжения, %;

U_2ном - номинальное напряжение вторичной обмотки, В;

U₂ – напряжение вторичной обмотки при различных нагрузках, В.
Величину ΔU_2% можно рассчитать по заданному коэффициенту нагрузки β, коэффициенту мощности cosφ₂ и напряжению короткого замыкания (КЗ) U_к, указываемого в паспорте трансформатора при неизменном напряжении U₁ на зажимах первичной обмотки. Коэффициент нагрузки по условиям задачи принимается β=0; 0,05; 0,1; 0,2; 0,4; 0,6; 0,8; 1. Формула имеет вид (2.8)


где β – коэффициент нагрузки;

U_ка% - активная составляющая напряжения КЗ, %;

cosφ₂ – коэффициент мощности;

U_кр% - реактивная составляющая напряжения КЗ, %.
Активную составляющую напряжения КЗ рассчитаем по формуле (2.9)


где U_ка% - активное напряжение КЗ, В;

U_к% - напряжение КЗ относительно фазного напряжения первичной обмотки, %

cosφ_к – коэффициент мощности КЗ.
Реактивную составляющую по формуле (2.10)


где U_кр% - реактивное напряжение КЗ, В;

sinφ_к – отношение реактивного сопротивления КЗ к полному.
Коэффициент мощности КЗ cosφ_к – это отношение активного сопротивления КЗ к реактивному. Тогда формула будет иметь вид (2.11)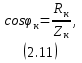


где R_к – активное сопротивление КЗ фазы трансформатора, Ом;

Z_к – полное сопротивление КЗ фазы трансформатора, Ом.
Активную составляющую сопротивления КЗ фазы найдем по формуле (2.12)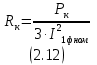


где R_к – активная составляющая сопротивления КЗ, Ом;

P_к - мощность потерь КЗ, Вт.
Подставив данные в (2.12), получим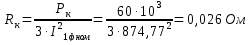

Формула для нахождения полного сопротивления КЗ фазы трансформатора имеет вид (2.13)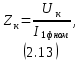


где Z_к – полное сопротивление КЗ, Ом;

U_к – напряжение КЗ, В.
Напряжение КЗ найдем по формуле (2.14)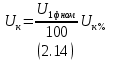


где U_к – напряжение КЗ, В.
Тогда, подставив значения в формулу (2.14), напряжение КЗ составит

Теперь, когда известно напряжение КЗ, можно рассчитать полное сопротивление по формуле (2.13)

Далее, имея все данные, можно рассчитать коэффициент мощности КЗ по формуле (2.11)

sinφ_к – это отношение реактивного сопротивления КЗ к полному. Так как реактивное сопротивление не известно, то найдем sinφ_к через cosφ_к (2.15).

Подставив данные в формулу (2.15), получим

Найдем активную составляющую напряжения КЗ по формуле (2.9). Подставив данные получим следующее значение

Значение реактивной составляющей

Теперь, имея все данные, можно рассчитать процентное изменение напряжения на вторичной обмотке по формуле (2.8) для разных значений коэффициентов нагрузки. При cosφ₂=0,8 угол между реактивным и полным сопротивлением составит 36,87º, т.е. sinφ₂=0,6.

При β=0

При β=0,2

Расчеты процентного изменения при остальных значениях коэффициента нагрузки β были выполнены с помощью ЭВМ и сведены в таблицу 2.2 (в таблице значения представлены как в процентах, так и в вольтах).

По полученным значениям изменения напряжения в процентах (ΔU_2%) можно определить напряжение на зажимах вторичной обмотки по формуле (2.16)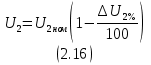

Подставив данные в формулу (2.16), рассчитаем напряжение на вторичной обмотке при разных значениях коэффициента нагрузки.

При β=0

Расчеты при остальных значениях коэффициента нагрузки β были выполнены с помощью ЭВМ и сведены в таблицу 2.2.

График внешней характеристики при cosφ₂=0,8 был построен по таблице 2.2 и представлен на рисунке 2.2.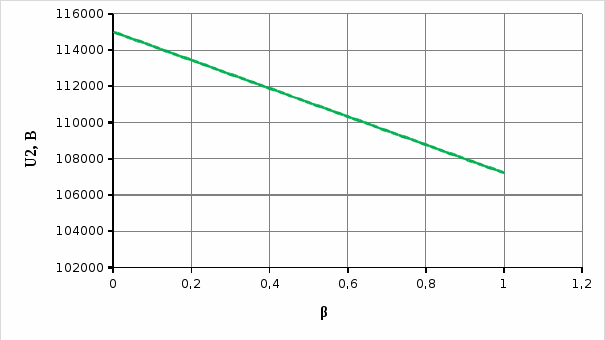


Рисунок 2.5 – Внешняя характеристика U₂=f(β) трансформатора при активно-индуктивной нагрузке (cosφ₂=0,8)

2.2.7 КПД трансформатора при активно-индуктивной нагрузке (cosφ₂=0,8). Построение характеристики η=f(β)

Чаще всего КПД трансформатора определяют косвенным методом, используя данные опытов холостого хода и короткого замыкания. Формула для определения КПД имеет вид (2.17)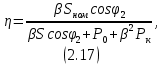


где η – КПД трансформатора;

β – коэффициент нагрузки;

S_ном – номинальная мощность трансформатора;

P₀ – мощность потерь холостого хода;

P_к – мощность потерь короткого замыкания.
Рассчитаем КПД трансформатора при разных коэффициентах нагрузках по формуле (2.17). По условию коэффициент нагрузки составляет β=0; 0,05; 0,1; 0,25; 0,5; 0,75; 1.

При β=0

При β=0,05

Дальнейшие расчеты КПД при остальных коэффициентах нагрузки были выполнены с помощью ЭВМ и представлены в таблице 2.2 (в процентах).
Таблица 2.2 – Результаты расчета КПД, изменения напряжения ΔU₂ напряжения на зажимах вторичной обмотки

β	η, %	ΔU2, %	ΔU2, В	U2, В
0	0	0	0	115000
0,05	96,6	-	-	-
0,1	98,21	-	-	-
0,2	98,98	1,354	1557,03	113442,97
0,4	99,27	2,708	3114,07	111885,93
0,6	99,26	4,062	4671,1	110328,9
0,8	99,19	5,416	6228,13	108771,87
1	99,08	6,77	7785,16	107214,84

График η=f(β) при cosφ₂=0,8 был построен по таблице 2.2 и представлен на рисунке 2.3.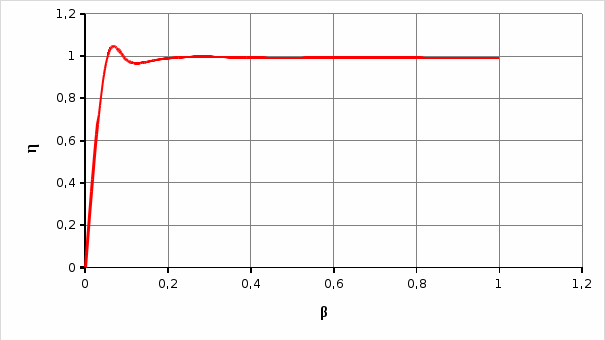


Рисунок 2.6 – График зависимости КПД трансформатора от коэффициента нагрузки η=f(β)

2.2.8 Определение нагрузки, при которой КПД имеет наибольшее значение

Анализ формулы (2.17) показывает, что КПД достигает максимального значения при такой нагрузке, когда магнитные потери равны электрическим потерям в обмотке (2.18)


где P₀ – магнитные потери, Вт.
Отсюда формула для коэффициента нагрузки, при которой КПД максимальное имеет вид (2.19)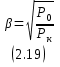

Подставив данные в формулу (2.19), получим

Теперь можно рассчитать максимальное КПД трансформатора по формуле (2.17)

2.2.9 Исследование возможности присоединения к зажимам вторичной обмотки несимметричной нагрузки

Присоединение несимметричной нагрузки к зажимам вторичной обмотки, которая соединена по схеме "треугольник", возможна, т.к. первичная обмотка соединена по схеме "звезда с нулем". При этом токи нулевой последовательности будут протекать в обеих обмотках. Поля, созданные этими токами, компенсируют друг друга, поэтому нейтраль фазных напряжений первичной обмотки не смещается. Фазные напряжения остаются симметричными.

2.2.10 Смысл понятия "Группа соединения обмоток" и его значение в данном трансформаторе

Группой соединения обмоток трансформатора называют условное число, характеризующее сдвиг фаз одноименных линейных напряжений обмоток НН, СН и ВН. Это число, умноженное на 30°, дает угол отставания в градусах векторов линейных напряжений обмоток НН и СН по отношению к векторам соответствующих линейных напряжений обмотки ВН. В обозначении трансформатора номер группы соединения указывается после обозначения схемы соединения обмоток, Y/Y-0, или Y/Δ-11 и др.

Для определения группы соединений используют аналогию со стрелочными часами, которая представлена на рисунке 2.5. Минутная стрелка часов совмещается с напряжением ВН и устанавливается на цифре 0 (12), а часовая совмещается с одноименным напряжением НН и указывает на группу соединения.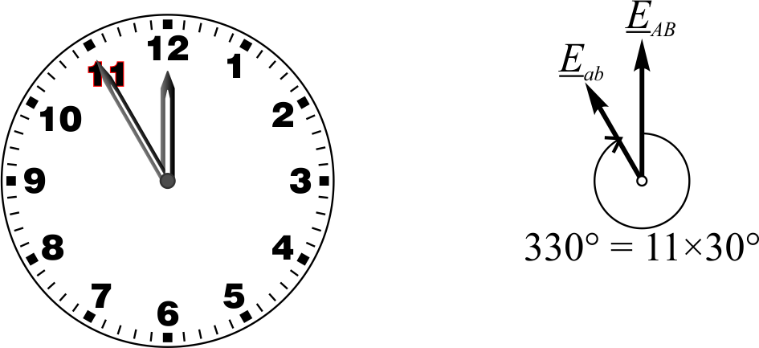


Рисунок 2.7 – Определение группы соединения обмоток трансформаторов

Нечетные группы (1, 3, 5, 7, 9, 11) получаются, если одна обмотка соединена в звезду, другая – в треугольник, а также, если одна обмотка соединена в зигзаг – звезду, а другая – в звезду.

Группа 11 означает, что сдвиг между векторами первичного и вторичного напряжения одноименных фаз составляет 11 часов, т.е. 330° (так как 30°*11=330°)