курсовой проект. Расчет характеристик трансформаторов и электрических двигателей з

• Название: Расчет характеристик трансформаторов и электрических двигателей з
• Анкор: курсовой проект
• Дата: 28.11.2021
• Размер: 0.78 Mb.
• Имя файла: Kursovoy_proekt_Dolzhenkov_A_A_AEb-19-1.docx
• Тип: Курсовой проект; #284091
• страница: 9 из 10

3.2 Расчет и исследование характеристик асинхронного двигателя

3.2.1 Паспортные данные

Паспортные данные двигателя представлены в таблице 3.1
Таблица 3 – Паспортные данные асинхронного двигателя

Номер варианта	Uном, В	f, Гц	Pном, кВт	nном, об/мин	ηном	cosφном	Iп/Iном	Mп/Mном	Mм/Mном
6	380	50	3	720	0,815	0,70	6	1,2	1,7

где U_ном – номинальное напряжение;

f – частота;

P_ном – номинальная мощность на валу двигателя;

n_ном – номинальная частота вращения;

η_ном – номинальный коэффициент полезного действия (КПД);

cosφ_ном – номинальный коэффициент мощности;

I_п/I_ном – кратность пускового тока;

M_п/M_ном – кратность пускового момента;

M_м/M_ном – кратность максимального момента.

3.2.2 Электрическая схема включения обмотки статора асинхронного двигателя

Так как линейное напряжение по варианту составляет 380 В, то двигатель соединен по схеме "звезда". Электрическая схема включения обмотки статора представлена на рисунке 3.6.


Рисунок 3.6 – Электрическая схема включения обмотки статора асинхронного двигателя.

3.2.3 Определение активной, реактивной и полной мощности, потребляемые двигателем из сети при номинальном режиме

Активная мощность, потребляемая из сети и полезная механическая мощность двигателя связаны между собой коэффициентом полезного действия по формуле (3.1)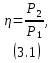


где η – КПД двигателя;

P₂ – полезная механическая мощность двигателя, В;

P₁ – мощность, потребляемая из сети, В.
Если условиться, что P₂=P_ном, то преобразовав формулу (3.1) для нахождения мощности P₁ получим выражение (3.2)


где P_ном – номинальная мощность на валу двигателя, В.
Подставив данные в формулу (3.2), получим

Полную мощность найдем по формуле (3.3)


где S – полная мощность, потребляемая из сети, ВА.

cosφ_ном – номинальный коэффициент мощности.
Подставив данные в формулу (3.3) значение полной мощности составит

Формула для нахождения реактивной мощности имеет вид (3.4)


где Q – реактивная мощность, потребляемая из сети, ВАр.
Подставив данные в формулу (3.4), получим

3.2.4 Номинальные и пусковые токи; номинальный пусковой и максимальный моменты

Номинальный ток найдем по формуле (3.5)


где I_ном – номинальный ток, А;

U_ном – номинальное напряжение, В;

η_ном – номинальное КПД.
Подставив данные в формулу (3.5) значение номинального тока составит

Пусковой ток найдем из кратности пускового тока, которая задана по условию задачи. По условию задано, что пусковой ток больше номинального в 4,5 раза. Учитывая это условие, значение пускового тока составит

Для нахождения момента используем формулу (3.6)


где M_ном – номинальный момент на валу двигателя, Нм;

ω_ном – номинальная угловая скорость, рад/с.
Угловую скорость найдем по формуле (3.7)


где n_ном – номинальная частота вращения двигателя, об/мин.
Подставив данные в формулу (3.7), получим

Теперь, имея все необходимые данные для нахождения номинального момента, подставим их в формулу (3.6) и получим

По паспортным данным двигателя пусковой и максимальный моменты имею кратность по отношению к номинальному значению.

Значение пускового тока составит

Значение максимального момента составит

3.3.5 Частота вращения магнитного поля статора, номинальное и критическое скольжение

Частота вращения магнитного поля статора при заданной частоте питающего напряжения обратно пропорциональна числу пар полюсов обмотки статора р. Формула имеет вид (3.8)


где n₀ – частота вращения магнитного поля статора, об/мин;

f₁ – частота питающего напряжения, Гц;

p – число пар полюсов.
Так как нам не известно число пар полюсов, то определим его по формуле (3.9)

Подставив данные в формулу (3.9), получим

Число пар полюсов должно быть целым, поэтому округляем его до ближайшего целого.

Теперь, подставив данные в формулу (3.8), значение частоты вращения магнитного поля составит

Зная частоту вращения магнитного поля и номинальную частоту вращения вала ротора, можно определить номинальное скольжение по формуле (3.10)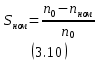

Подставив значения в формулу (3.10), номинальное скольжение составит

В инженерной практике для расчета механической характеристики асинхронного двигателя часто применяется упрощенная формула Клосса, которая имеет вид (3.11)


где M_i, S_i – i-е значение вращающего момента и скольжения на механической характеристике;

M_к – максимальный момент, Нм.
Если в формуле (3.11) вместо M_i и S_i подставить номинальные значения момента M_ном и скольжения S_ном, то можно определить величину критического скольжения S_к. Например, может быть получено выражение вида (3.12)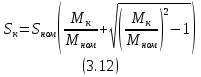

Тогда значение критического момента составит

3.3.6 Полные потери мощности при номинальном режиме работы

По паспортным данным суммарные потери в номинальном режиме определяются с учетом номинального значения КПД, и формула представляется в виде (3.13)


где P_ном – номинальная мощность на валу двигателя;

η_ном – номинальное КПД двигателя.
Подставив данные в формулу (3.13), суммарные потери в номинальном режиме составят

3.3.7 Расчет и построение зависимости частоты вращения ротора двигателя от величины механического момента, приложенного к валу

Для исследования зависимости частоты вращения или скольжения ротора двигателя от величины механического момен­та, приложенного к валу, можно воспользоваться упрощенной формулой Клосса (3.11).

Расчет будем производить до значения S=1,1S_к, т.к. дальше будут большие погрешности. Погрешности связаны с тем, что формула Клосса дает приближенные результаты и при скольжении S=1 погрешность достигает 200-300%.

При S=0,04

Угловую скорость вращения найдем по формуле (3.14)


где ω_i – i-я угловая скорость вращения, рад/с;

ω₀ – угловая скорость магнитного поля статора, рад/с;

S_i – i-е значение скольжения.
Подставив значения в формулу (3.14), получим

Дальнейшие расчеты были выполнены с помощью ЭВМ и представлены в таблице 3.2. Зависимость угловой скорости вращения ротора двигателя от величины механического момента была построена по таблице 3.2 и представлена на рисунке 3.7.

3.3.8 Исследование зависимости частоты ЭДС и тока, электрических потерь в роторе от скольжения

Зависимость частоты ЭДС и тока ротора от скольжения можно получить, используя соотношение (3.15)


где f₂ – частота ЭДС и тока ротора, Гц;

f₁ – частота питающего напряжения, Гц;

S_i – i-е значение скольжения.
При S=0,04

Формула для нахождения мощности, передаваемой от статора к ротору, имеет вид (3.16)


где P_эм – мощность, передаваемая от статора к ротору, Вт
Подставив данные в формулу (3.16), получим

Электрические потери в роторе и мощность, передаваемая от статора к ротору, имеют связь через скольжение. Она имеет вид (3.17)


где ΔP_эл2 – электрические потери в роторе, Вт.
Рассчитаем по формуле (3.17) для разных значений скольжения электрические потери в роторе.

При S=0,04

Расчеты для остальных значений скольжения были выполнены с помощью ЭВМ и представлены в таблице 3.2.

Графики зависимости частоты ЭДС и тока, электрических потерь от скольжения представлены на рисунках 3.8 и 3.9.
Таблица 3.2 – Результаты расчета

Si	0	0,04	0,08	0,12	0,16	0,2	0,24	0,28	0,32	0,36	1
Mi, Н*м	0	72,19	138,47	194,42	237,93	269	289,05	300,14	304,39	303,68	263,08
ωi, рад/с	157	150,72	144,44	138,16	131,88	125,6	119,32	113,04	106,76	100,48	0

Продолжение таблицы 3.2

f2, Гц	0	2	4	6	8	10	12	14	16	18	50
ΔPэл2, Вт	0	869,6	1739,1	2608,7	3478,3	4347,8	5217,4	6086,9	6956,5	7826,1	21739

Рисунок 3.7 – График зависимости угловой скорости вращения двигателя от механического момента ω=f(M)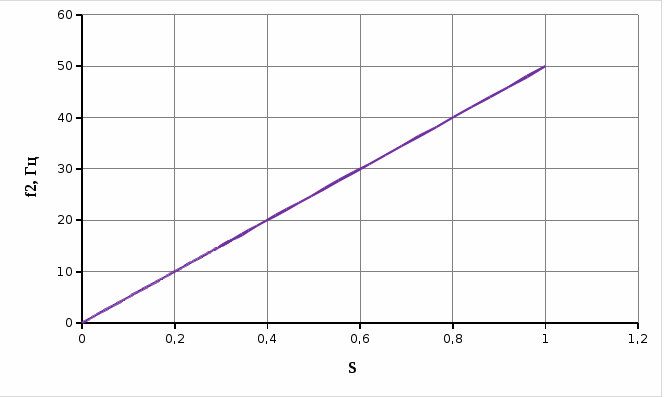


Рисунок 3.8 – График зависимости частоты ЭДС и тока от скольжения f₂=f(S)


Рисунок 3.9 – График зависимости электрических потерь в роторе от скольжения ΔP_эл2=f(S)

Вывод

В данной задаче курсового проекта были рассчитаны характеристики асинхронного двигателя, а именно активная, реактивная и полная мощности, найдены номинальные и пусковые токи, номинальный, пусковой и критический моменты, номинальное и критическое скольжение, рассчитаны полные потери в двигателе, построены механическая характеристика и исследована зависимость частоты ЭДС и тока, электрических потерь в роторе от скольжения.

Механическая характеристики были построены в двигательном режиме. Это можно определить по знаку скольжения и момента. В двигательном режиме они имеют положительное значение, а в генераторном отрицательное. На механической характеристике отчетливо видно, что при достижении определенного значения момента скорость двигателя начинает резко падать, момент также уменьшается. Этот момент соответствует критическому значению, т.е. когда S=S_к. До достижения данного значения скорость двигателя спадает линейно. Механическая характеристика совпадает с теоретической естественной механической характеристикой, которая была показана в разделе 3.1.4, т.е. расчеты были произведены правильно.

Графики зависимости ЭДС и тока, электрических потерь от скольжения имеют линейных характер. Также было выяснено, что формула Клосса имеет довольно большие погрешности, поэтому точки для построения механической характеристики рассчитывались до значения 1,1S_к и совмещены с точкой, при которой S=1. Из таблицы 3.2 видно, что до достижения критического скольжения момент увеличивался, а после его достижения уменьшается, также ясно, что при достижении номинального скольжения момент и угловая скорость также принимают номинальное значение. Полные потери двигателя были вычислены с помощью КПД, но их также можно было найти как разность мощностей P₁ и P₂. Частота вращения магнитного поля статора, а следовательно и ротора, напрямую зависит от числа пар полюсов и частоты питающей сети.