РАСЧЕТ НАДЕЖНОСТИ АВТОМАТИЧЕСКИХ УСТРОЙСТ6. Расчет надежности автоматических устройств

• Название: Расчет надежности автоматических устройств
• Дата: 25.12.2021
• Размер: 1.14 Mb.
• Имя файла: РАСЧЕТ НАДЕЖНОСТИ АВТОМАТИЧЕСКИХ УСТРОЙСТ6.doc
• Тип: Документы; #317633
• страница: 7 из 7

Надежность АСУТП.
Надежность является комплексным свойством объекта, включающим четыре составляющие:безотказность, ремонтопригодность, сохраняемость, долговечность.Каждая из составляющих связана с некоторой случайной величиной, имеющей размерность времени:Тб-время безотказной работы;Тв-время восстановления работоспособности;Тс- время сохранения объектом своих технических характеристик;Тд- время от начала эксплуатации до первого отказа (или между отказами).

Вследствие случайного характера перечисленных величин чаще используют их математические ожидания: среднее время безотказной работы Т_б , среднее время восстановления Т_в , среднее время сохраняемости Т_с , средний срок службы Т_сс и средний ресурс Т_р , а также интегральные функции распределения для фиксированного значения t : вероятность безотказной работы объекта р() в интервале 0,, вероятность восстановления работоспособности объекта F_в () после отказа за время , вероятность сохранности объекта G_с () в течение заданного времени , вероятность G_сс () или G_р () того, что срок службы объекта (его ресурс) превысит заданное время . Применяют также комплексные показатели надежности: коэффициент готовности К_г = Т_б /( Т_б + Т_в ), коэффициент технического использования К_ти = Т_б /( Т_б + Т_в +r_то_то) (здесь r_то – средняя продолжительность одного сеанса технического обслуживания); _то – коэффициент интенсивности технического обслуживания).

Описание надежности АСУ ТП базируется на функциональном подходе, согласно которому надежность АСУ ТП представляет собой совокупность характеристик надежности и показателей по всем функциям системы. Перечень и определение функций, по которым рассматривается надежность, даются в техническом задании на АСУ ТП.

С точки зрения надежности функции АСУ ТП разбиваются на две группы: непрерывные функции (Н – функции) двух видов, для выполнения которых необходимо непрерывное функционирование участвующих в их реализации средств системы в течение расчетного интервала, и функции – процедуры (П – функции), выполнение которых сводится к эпизодической реализации некоторой процедуры в заранее определенные моменты времени или при поступлении запросов.

Н – функции первого вида ( выполнение некоторых действий) имеют характеристические случайные величины; - время безотказного выполнения системой i – й функции; - время восстановления работоспособности по i – й функции; - наработка системы на отказ i – й ; р_i () – вероятность безотказной работы i –й функции в течение заданного времени ; () – вероятность восстановления в течение заданного времени  работоспособности системы по i-й функции; К_ти- коэффициент технического использования системы по i-й функции.

Н- функции второго вида (достижение некоторого результата, выраженного в удельных технических или экономических показателях) включают понятия удельной (часовой) эффективности системы _I i-й функции и удельной (часовой) эффективности системы Е_t в момент t, связанных между собой соотношением

m

Е_t=y_st_t (где m- общее число выполняемых системой Н-функции первого

S=1

вида: y_st- двоичная переменная 1;0).

Н-функция второго вида определяется как обеспечение пребывания системы на некотором уровне Е_i или в некотором интервале уровней (Е_i, Е_j), в качестве которых принимаются уровни эффективности системы в различных состояниях. Комплексным показателем надежности по н-функциям второго вида является надежностный коэффициент снижения эффективности.
Надежность элементов АСУ ТП.
Объекты пищевой промышленности по видам допускаемых отклонений параметров можно разделить на три группы.К первой относятся такие технологические параметры, для которых недопустимы сверхпредельные отклонения при любых режимах работы, так как это приводит к порче либо продукта, либо оборудования.У параметров второй группы допустимы кратковременные сверхдопустимые отклонения (не вызывающие аварии ), критерием оценки качества управления служат интегральные или усредненные показатели.К третьей группе относятся параметры , для которых предусмотрены как динамические , так и статические допуски.

Например, для линейных систем автоматической стабилизации (к которым относятся около 80% локальных систем кправления в пищевой промышленности) обработка приборной записи процесса управления позволяет определить такие параметры, как математическое ожидание и дисперсия ² регулируемого параметра, а также среднее число выбегов параметра за границы динамического допуска _д:

N=c exp (-_д²/2²)/. (1.78)

Величины ² и _д связаны между собой , а также с длительностью одного динамического отказа:

(1.79)


где с=_/, _²- дисперсия скорости изменения параметра.

Надежность как средство повышения эффективности АСУ ТП.

Как указывалось, повышение надежности системы является одним из средств повышения уровня эффективности системы.Непосредственно влияя на эффективность, надежность выступает как один из важнейших факторов, определяющих эффект от использования АСУ ТП.В связи с этим при проектировании различных частей системы возникают две взаимосвязанные задачи: определить для данной части экономически рациональный уровень надежности и потребные для его реализации средства (как технические, так и денежные );имеющиеся материальные ресурсы так распределить между отдельными устройствами, обеспечивающими надежность, чтобы получить ее максимальное значение.Пример рассмотрен ниже.

Для работающего объекта можно выделить ряд состояний, в том числе нормальную эксплуатацию (при которой объект приносит определенный доход), состояние отказа и восстановления эффективности (обслуживание), в процессе которых образуются экономические потери.Различают три рода потерь от отказов системы управления за период эксплуатации t:

Потери первого рода П¹(t) представляют собой потери только условно-годовой экономии, которая могла быть получена на объекте при нормальном функционировании;

Потери второго рода П¹¹(t) складываются помимо потерь условно-годовой экономии также из потерь прибыли, которую получило бы предприятие при нормальном функционировании объекта;

Потери третьего рода П¹¹¹(t) включают дополнительно к перечисленным также потери, равные себестоимости изготовленного и испорченного продукта за тот же период.

Общие потери от отказов всех видов

П (t)= П¹(t)+ П¹¹(t)+ П¹¹¹(t). (1.80)

Вынужденный простой оборудования и управляющего устройства вследствие его отказов за период t вызывает ущерб

У(t)=У¹(t)+ У¹¹(t)+ У¹¹¹(t), (1.81)

где У¹(t)- ущерб первого рода из-за вынужденного простоя только управляющего устройства; У¹¹(t)- ущерб второго рода, когда из-за отказа управляющего устройства простаивает система в целом; У¹¹¹(t)- ущерб третьего рода, обусловленный вынужденным простоем управляющего устройства и управляемого объекта.

Общие потери от отказов и ущерб составляют вместе показатель экономических последствий отказов системы управления

ЭПО(t)=П(t)+У(t). (1.82)

Для обеспечения максимальной эффективности функционирования управляемого объекта стремятся так организовать систему его управления, контроля и восстановления, чтобы объект не только находился в области допустимых состояний, но и максимизировал критерий эффективности Э функционирования объекта.

Для систем контроля и управления эффективность функционирования управляемого объекта можно оценить величиной средней эффективности

(где Т – интервал усреднения). (1.83)

Под величиной Э подразумевают либо экономический показатель работы объекта, либо связанный с ним технический показатель, например, логарифмическую меру вероятности Р работоспособности объекта.

Типичная задача рационального проектирования устройств и систем обеспечения надежности заключается в распределении ограниченной суммы средств между отдельными устройствами системы контроля и управления, обеспечивающими работоспособность некоторой функции объекта, или между несколькими вариантами (уровнями) системы контроля.

Пусть известны х_i – величины средств, вкладываемых в системы, n- число вариантов (i=1,…,n), а также определено n функций с неотрицательными значениями: f₁(х₁), где х₁d₁; f₂(х₂), где х₂d₂;… f_n(х_n),где х_nd_n.Требуется так выбрать значения аргументов х₁,…, х_n, чтобы обеспечить экстремум функции

F(х₁,…, х_n)= f₁(х₁)+…+ f_n(х_n), причем на х₁,… х_n х_n накладывается система ограничений, предполагающая существование экстремума F.Для данного случая система ограничений определяется как х₁+ х₂+…+ х_n =К (где х_i- размеры средств, вкладываемых в отдельные варианты системы, К- общая сумма средств, выделенная на всю систему).

Оптимальный вариант вложения ( распределения) средств определяется экстремумом функции

(К)=extr f₁(х₁)+…+ f_n(х_n). (1.84)

Функция (К) рассчитывается пошаговым методом, причем на первом шаге ищется экстремум суммы f₁+ f₂ для всех х₁,х₂, которые составляют всех х₁+х₂=К. На втором шаге отыскивается экстремум функции F_1,2 и f₃ для различных х₁,х₂ и х₃, таких, что сумма х₁+х₂+х₃=К и т.д. до тех пор, пока не будут перебраны все варианты.

Рассмотрим пример, относящийся к вложению ограниченной суммы средств, которую следует распределить между тремя возможными каналами системы контроля, входящей в АСУ ТП спиртового производства.По намеченной структуре системы и известным характеристикам надежности входящих в нее приборов и средств автоматизации находится вероятность Р безотказной работы каждого канала системы при различной стоимости входящих в канал контроля и управления средств.

Зависимости Р(К) могут быть заданы аналитически или графически, как, например, на рис. 1.16 для трех каналов (а,б,в) системы.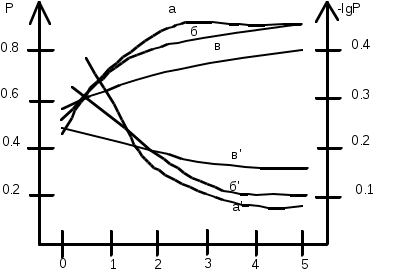

Рис.1.16 График для расчета надежности системы контроля и управления.
Распределение средств между каналами системы контроля и обслуживания.

Таблица 1.9

Каналы системы и логарифмическая мера вероятности	Варианты вложения средств
	1	2	3	4	5
а, тыс.те б, тыс.те -lg Pa -lg Pб -lg (PaPб)	0 4 0,36 0,04 0,40	1 3 0,16 0,07 0,23	2 2 0,08 0,11 0,19	3 1 0,04 0,19 0,23	2 2 0,02 0,32 0,34

Общий критерий эффективности

Э=-lgP=-(lgP_a + lgP_б+ lgP_в), (1.85)

где P_a ,P_б и P_в – вероятности работоспособности каналов.

Пусть на всю систему предполагается затратить сумму К=4 тыс.те., причем для упрощения расчетов будем считать, что средства распределяются дискретно с шагом 1000 те.Согласно условию задачи требуется так распределить общую сумму К между каналами а,б,в, чтобы минимизировать критерий Э:
Э*=min(-lg Pi), (1.86)

Ki i

что соответствует максимуму работоспособности всей системы.

При распределении общей суммы К=4 тыс.те может быть пять вариантов, приведенных в табл.Там же даны величины логарифмической меры по каждому варианту распределения к между каналами а и б, а также общее значение критерия Э Э=-lg(P_aP_б).

Величины мер вероятности получены из графика рис., в случае задания критерия Э(Р) в аналитическом виде величины Э были бы рассчитаны по прилагаемым формулам .

Из табл.1.9 Видно , что значение Э , соответствующее максимуму работоспособности, минимальное в третьем варианте распределения средств.

На следующем этапе общую сумму К распределяют между тремя каналами а, б, и в таким образом, чтобы средства выделенные на каналы а и б, распределялись между ними так, как это получено на первом шаге расчета. Выбрав из графиков рис.1.16 Значения меры вероятности Р и рассчитав соответствующую величину общего критерия Э=-lg(Р_аP_бP_в), легко убедиться , что минимальное значение Э достигается в варианте распределения средств между каналами а, б и в в 2,2 и 0 тыс.те соответственно и составляет 0,44.При любом другом варианте распределения величина Э растет , а работоспособность объекта снижается. Аналогичный расчет производится и при любом другом числе каналов системы контроля и управления и другой сумме средств, отпущенных на систему.