РАСЧЕТ НАДЕЖНОСТИ АВТОМАТИЧЕСКИХ УСТРОЙСТ6. Расчет надежности автоматических устройств
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
|
ЗНАЧЕНИЕ КОНТРОЛЯ ДЛЯ РЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ ОБЪЕКТОВ. В восстанавливаемых системах для получения максимального эффекта от применения резервирования необходима идеальная система контроля, мгновенно обнаруживающая появление неработоспособного состояния любого элемента. В действительности обычно контролем охвачена лишь часть элементов (неполнота контроля) и возможны ложные сигналы о неработоспособности системы из-за отказов аппаратуры контроля или ошибок людей, неправильно оценивающих показания приборов (неидеальность контроля). а) Значение контроля для объектов, допускающих перерывы в работе. Для нерезервированной восстанавливаемой системы аппаратура контроля влияет в основном на коэффициент готовности. Рассмотрим систему, находящуюся в дежурном режиме. Предположим, что законы распределения времени безотказной работы и времени восстановления всех элементов являются показательными. Обозначим интенсивность отказов контролируемой части системы 1, неконтролитуемой части системы 2, интенсивность ложных сигналов о неработоспособности системы 3; 4 – интенсивность отказов системы в ходе проверки по ложному сигналу (возможны условия проверки, при которых 41+2);интенсивность восстановления системы 1, аппаратуры контроля 2, интенсивность восстановления системы вместе с аппаратурой контроля 3. Рассматриваемая система может находиться в произвольный момент t в одном из следующих несовместимых состояний:0- система нормально функционирует;1- система неработоспособна ,находится в ремонте ;2- система неработоспособна ,но аппаратура контроля не обнаружила;3- работоспособная система проверяется по ложному сигналу от аппаратуры контроля;4- неработоспособны и восстанавливаются система и аппаратура контроля. Графы состояний восстанавливаемой системы с аппаратурой контроля приведены на рис.1.6 а)   1 2 3 4            2 21 3 б) 1 3 4            2 21 3 в) 1 3        2 21 По графу состояний может быть составлена система дифференциальных уравнений для вероятностей состояний и получено выражение для функции готовности Г(t).Однако в общем случае для рис.,а получается громоздкое выражение. В частном случае рис ,б полного контроля (все элементы охвачены контролем , 2=0) коэффициент готовности (стационарная вероятность нахождения в состоянии 0). 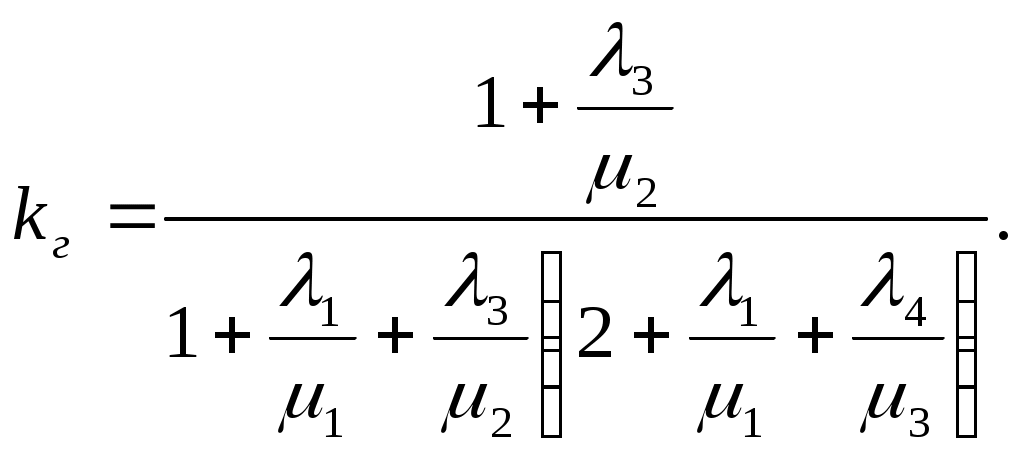 (1.43) (1.43)Когда система не отказывает в течение проверки по ложному сигналу и осуществляется полный контроль (2=0, 4=0), граф состояний имеет вид рис,в. При этом коэффициент готовност 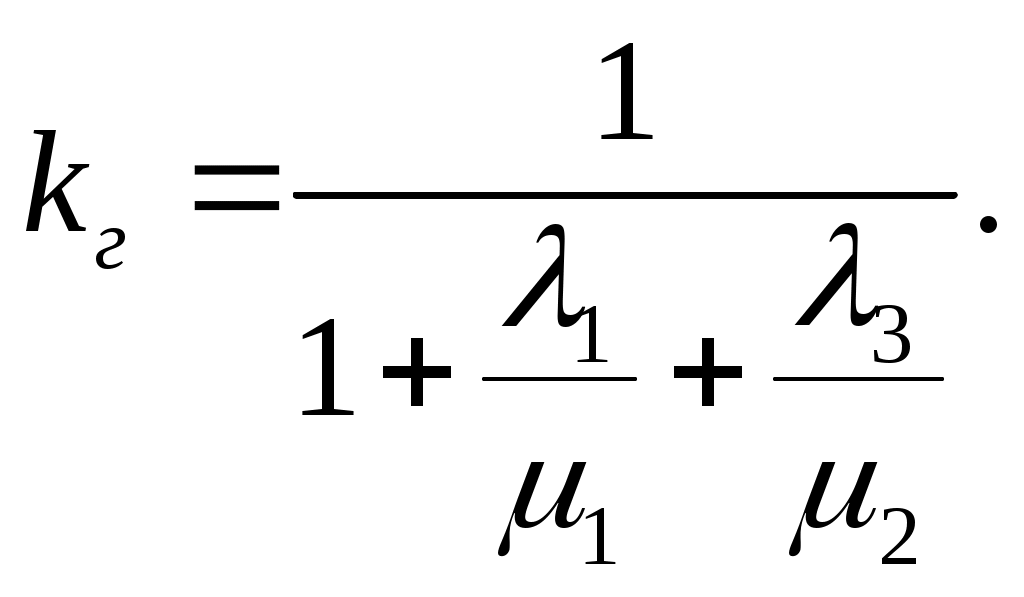  (1.44) (1.44)Для резервированных восстанавливаемых систем аппаратура контроля существенно влияет на все показатели надежности систем, в том числе на среднюю наработку до отказа, вероятность безотказной работы и др. Рассмотрение вопроса в общем случае является очень сложным. Чтобы выявить роль полноты охвата контролем, рассмотрим частный случай надежной аппаратуры контроля (3=0) в дублированной восстанавливаемой системе. Рассматриваемая система может находиться в произвольный момент времени t в одном из следующих несовместимых состояний:0- оба элемента работоспособны ;11- один из элементов отказал из-за контролируемой части его;12- один из элементов отказал из-за неконтролируемой части его;2- система неработоспособна. Граф состояний системы приведен на рис.,а.Состояние 2 считается поглощающим, =1+2 – интенсивность отказов одного элемента.Получаем выражение для среднего времени безотказной работы системы: 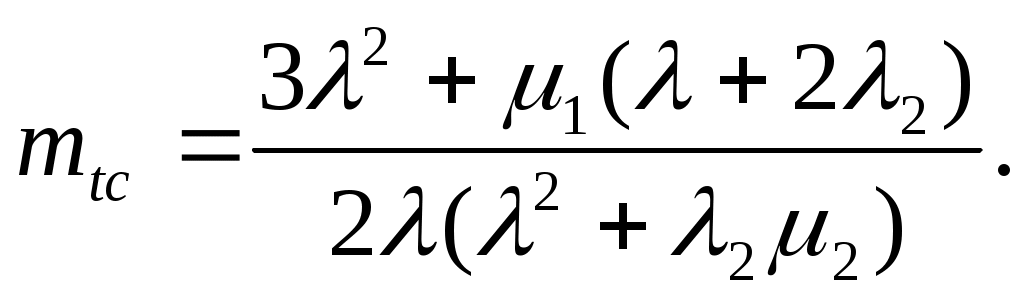 (1.45) (1.45)При полном контроле элементов 2=0 и среднее время безотказной работы системы Сопоставив и ,получим, что из-за неполноты контроля среднее время безотказной работы уменьшается,составляя лишь долю от возможного m’tc: 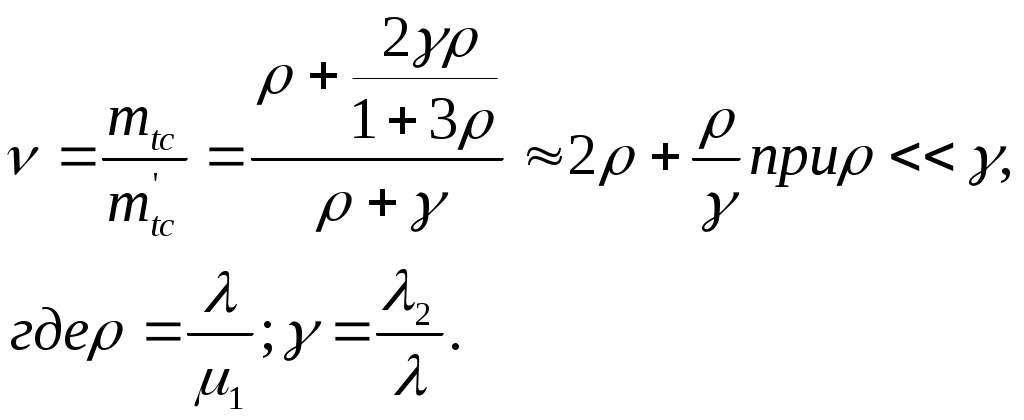 (1.47) (1.47)В  реальных системах значения обычно менее 0,01.Зависимости от коэффициента при различных значениях приведены на рис.1.7,б. реальных системах значения обычно менее 0,01.Зависимости от коэффициента при различных значениях приведены на рис.1.7,б.а)   11 21 22 1 11 21 22 1     1 1     б) = =0,02;0,01;0,001. 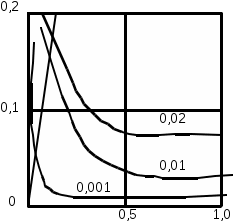 Рис.1.7 К вопросу о влиянии полноты контроля на эффект от применения резервирования в восстанавливаемой системе, допускающей перерывы в работе. а- граф состояний дублированной системы при абсолютно надежной аппаратуре контроля (2=0); б- зависимость отношения значений среднего времени безотказной работы при неполном и полном контроле от коэффициента =2/. На рис. 1.7,б пунктиром проведена прямая =() дают характерное значение *.При <* полнота охвата контролем существенно влияет на среднее время безотказной работы системы.В этой области даже небольшое уменьшение ведет к значительному увеличению среднего времени безотказной работы системы.При >* эффект от применения резервирования меньше в десятки раз , при этом значение полноты контроля уменьшается.Из графика на рис. ,б следует,что для наиболее часто встречающихся на практике значений =0,01-0,001 значения * лежат в диапазоне 0,03-0,11. б) Значение контроля для объектов, не допускающих перерывов в работе. Рассмотрим восстанавливаемую систему с ненагруженным активным дублированием.Структурная схема системы изображена на рис.,а.В этой системе в переключающем устройстве можно выделить контролирующее (КУ) и исполнительное (ИУ) устройства. Надежность переключающего устройства определяется в основном контролирующим устройством, которое может иметь два типа отказов: отказ типа «ложное переключение» , при котором работоспособный основной элемент отключается и включается резервный; отказ типа «отсутствие переключения» , при котором не включается в работу резервный элемент, если откажет работающий. а    ) )ОЭ РЭ          КУ ИУ                б)   (1-+1) (1-+1)    2 2        Рис.1.8 К вопросу о значении контроля в восстанавливаемой системе с ненагруженным активным дублированием. а- блок-схема система; ОЭ- основной (работающий) элемент; РЭ- резервный элемент; ИУ- исполнительное устройство; КУ – контролирующее устройство; б- граф состояний при безотказном исполнительном устройстве, двух видах отказов контролирующего устройства и неполном контроле. Пусть интенсивность отказов переключателя (контролирующего устройства) пропорциональна интенсивности отказов работающего элемента , причем интенсивность отказов первого типа 1, второго типа 1, 1 + 2=. Контролем охвачена лишь часть работающего элемента. Часть отказов работающего основного элемента переключающее устройство не реагирует.Обозначим, как и ранее, долю неконтролируемых отказов основного элемента , т.е. неконтролируемые отказы имеют интенсивность . Рассматриваемая система может находиться в произвольный момент времени в одном из несовместимых состояний: 0- работает основной элемент, переключатель работоспособен; 1 – неработоспособна контролируемая часть основного элемента при работоспособном переключателе или произошло ложное срабатывания переключателя; работает резервный элемент ; 2 – работоспособен основной элемент, произошел отказ переключающего устройства второго типа (переключение невозможно); 3 – подмножество состояний, соответствующих отказу системы. Основную часть времени восстановления системы составляет время поиска неисправности.В первом приближении будем считать, что интенсивность восстановления одинакова для всех блоков системы и равна . Граф состояний рассматриваемой системы приведен на рис.1.8,б.Этому графу соответствует система дифференциальных уравнений для вероятностей состояний: 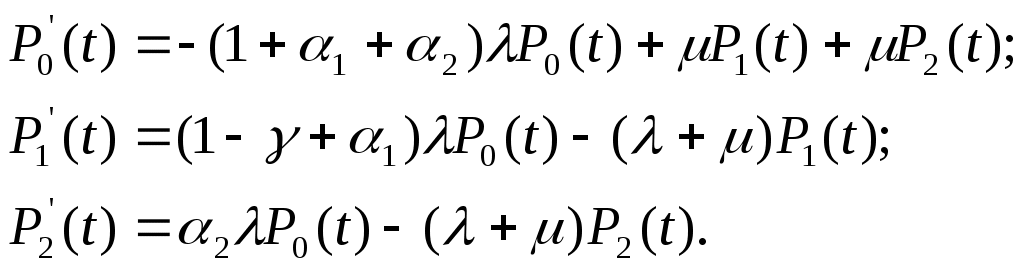 (1.48) (1.48)с нормировочным условием Решив эту систему уравнений при начальных условиях Р0(0)=1; Р1(0)= Р2(0)= Р3(0)=0, можно найти вероятность безотказной работы системы в течение заданного интервала (0,ti): Используя преобразование Лапласа , получаем: 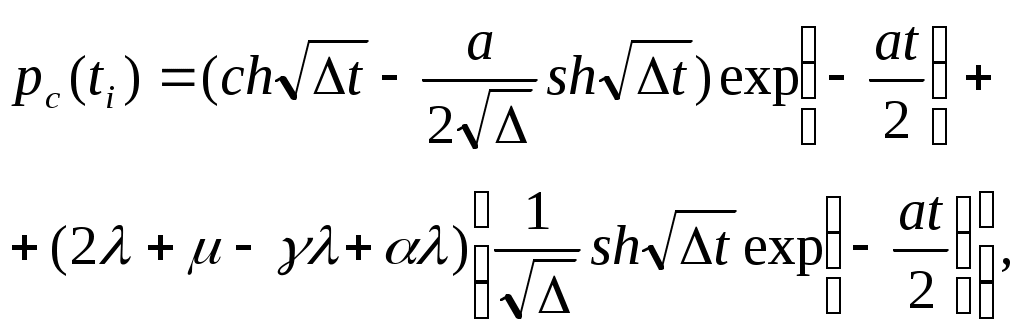 (1.51) (1.51)где Средняя наработка до отказа системы Учитывая, что обычно <<, получаем: Повышение надежности устройств достигается также выбором высоконадежных комплектующих элементов, герметизацией, кондиционированием, высокой культурой изготовления и эксплуатации изделия. Расчет надежности автоматических устройств на этапе технического проектирования проводится в зависимости от характера исходных данных о надежности элементов. Для определения надежности автоматического устройства необходимо знать: структуру устройства; число элементов с разбивкой их по типам, режимы работы и внешние условия; зависимости интенсивности отказов элементов от режима работы и внешних условий. Различают несколько типовых структур для расчета надежности по способу соединения элементов в устройстве: последовательно – параллельная структура; мостиковая структура; иерархическая структура и др. РАСПРЕДЕЛЕНИЕ НОРМ НАДЕЖНОСТИ СИСТЕМЫ ПО ЭЛЕМЕНТАМ. Так называется проводимый на начальном этапе проектирования процесс задания значений показателей надежности блоков и узлов системы но имеющемуся в техническом задании значению показателя надежности всей системы. В этот период информация о системе еще невелика, поэтому применяют довольно грубые приемы. По мере появления новых сведений вычисленные ранее значения уточняются. Существуют различные приемы распределения показателей надежности, которые рассмотрим на конкретных примерах: по принципу равнонадежности элементов; с учетом существующего соотношения показателей надежности элементов; с учетом перспектив совершенствования элементов; с учетом стоимости проектирования, производства и эксплуатации элементов. Выбор того или иного способа распределения показателей надежности зависит от имеющейся информации о проектируемом объекте. Пример 1-1. Для проектируемого усилителя задана вероятность безотказной работы в течение t1=2000 ч, равная pyc(t1)=0,98. Усилитель состоит из трех равнонадежных последовательных каскадов. Необходимо задать значение интенсивности отказов одного каскада. Решение. Так как каскады равнонадежны, имеем: В соответствии с условием примера откуда Для одного каскада интенсивность отказов должна быть Пример 1-2. Проектируемый объект состоит из трех блоков Л1, S1, C1. Для безотказной работы объекта необходима безотказная работа всех блоков. Задана вероятность безотказной работы объекта в течение t1=100 ч, равная pоб(t1)=0.97. Назначить требуемые значения интенсивностей отказов блоков λa1, λb1, λc1, если при рассмотрении прототипа объекта установлено, что блоки A0, В0, С0, аналогичные проектируемым, имеют интенсивности отказов λa0=10-4 1/ч; λb0=8∙10-4 1/ч; λc0= 3∙10-4 1/ч. Решение. Для распределения значений показателей надежности по блокам учтем существующее соотношение интенсивностей отказов блоков прототипа. При основном (последовательном на логической схеме) соединении блоков доля отказов объекта из-за отказов j-го блока где λоб — интенсивность отказов системы (всего объекта); λj — интенсивность отказов j-го блока (см. § 5-1). Коэффициент kj можно найти по соотношению интенсивностей отказов прототипа: 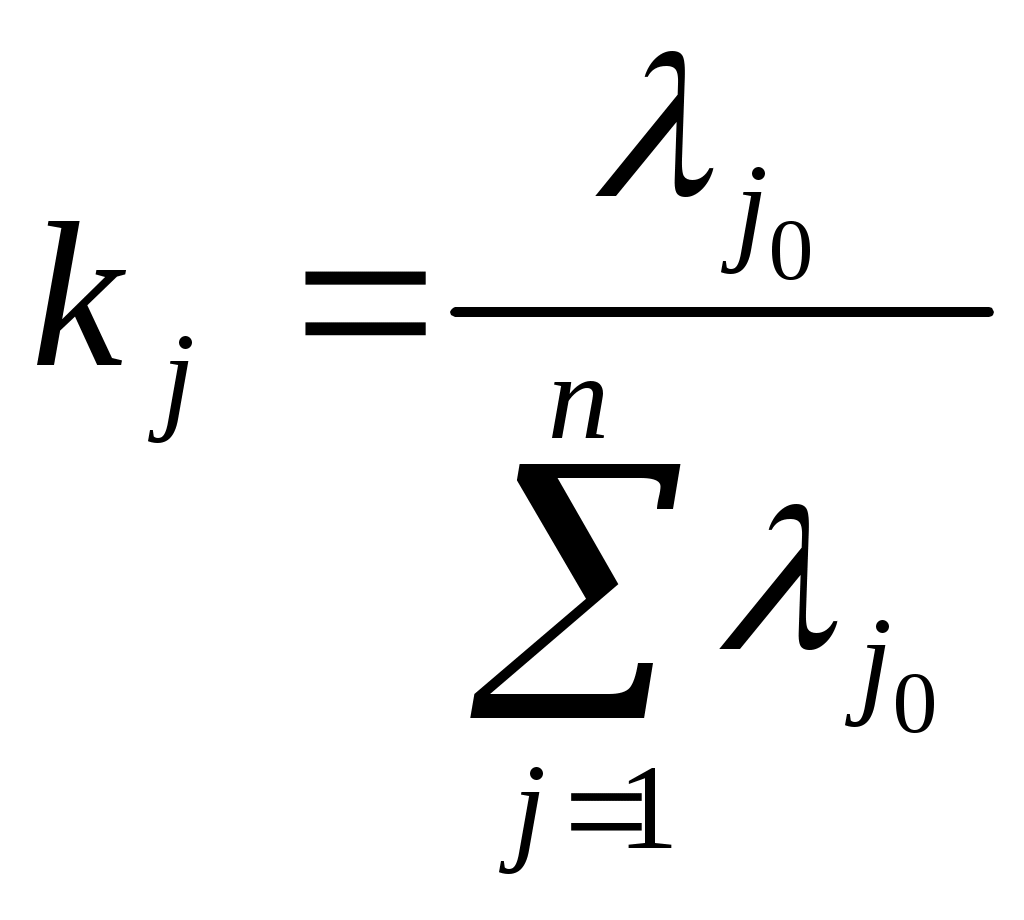 где n — число элементов. В рассматриваемом случае 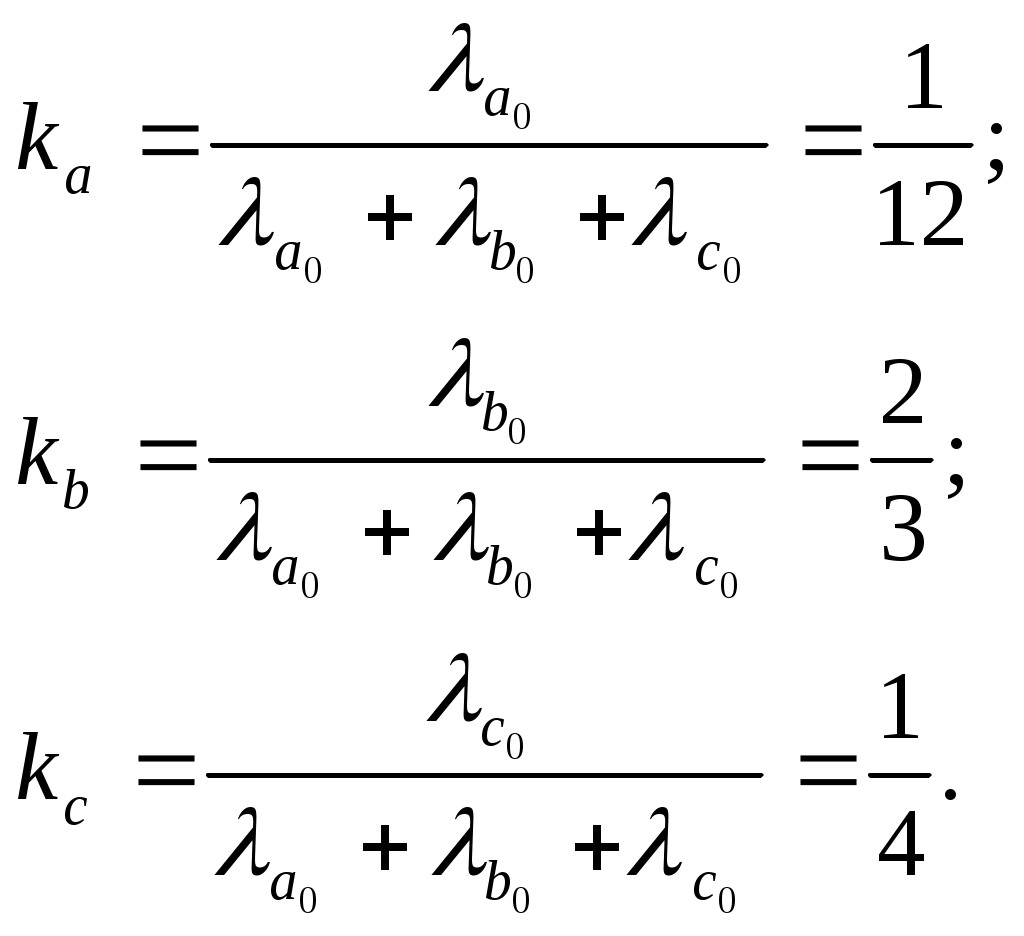 Значение λоб находим из соотношения 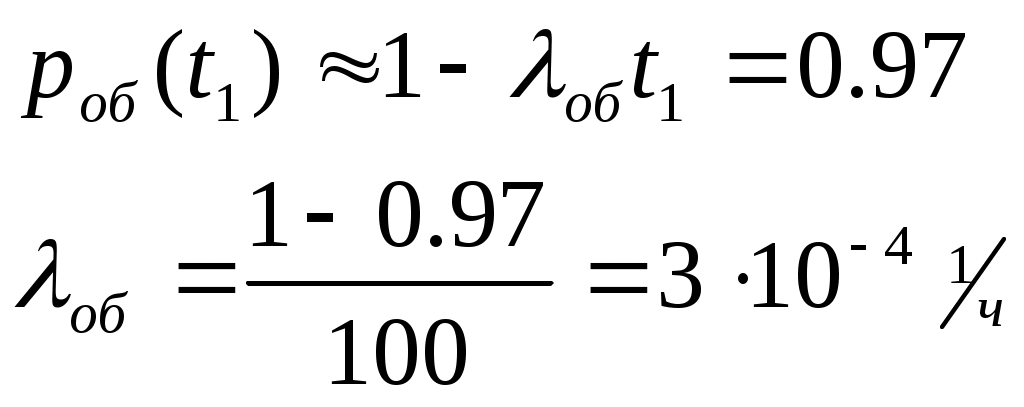 Нормы надежности для блоков 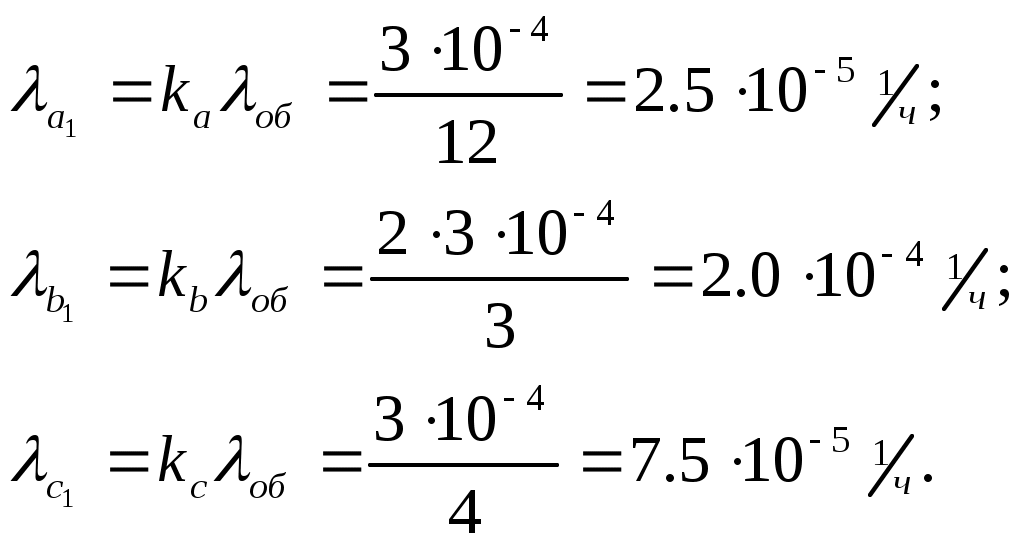 Пример 1-3. Проектируемый объект состоит из двух блоков А и В. Для безотказной работы объекта необходимо, чтобы оба блока были в работоспособном состоянии. Задана вероятность безотказной работы объекта в течение t1=100 ч; p(t1)=0,98. Назначить требуемые значения интенсивностей отказов блоков λa1, λb1, если в результате анализа данных за 1965—1980 гг. известно, что изменение интенсивностей отказов блоков аналогичных А и В прототипов Aо и Во по годам выпуска может быть аппроксимировано формулой где λ65 — интенсивность отказов изделия, выпущенного в 1965 г., l — год выпуска блока. Для блока А0: Для блока Во: Решение. Имеющееся соотношение показателей надежности блоков прототипа может значительно измениться за время проектирования и изготовления объекта. Экстраполируя значения интенсивностей отказов блоков-прототипов до 1980 г., получаем: 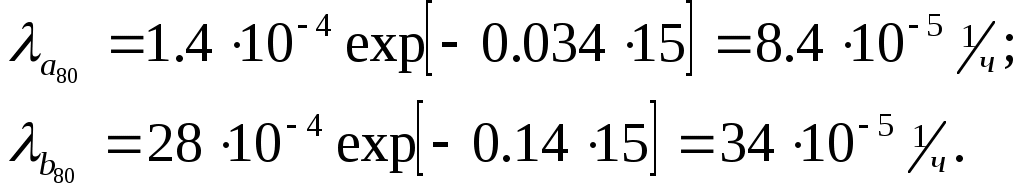 Далее аналогично примеру 3-2 имеем: 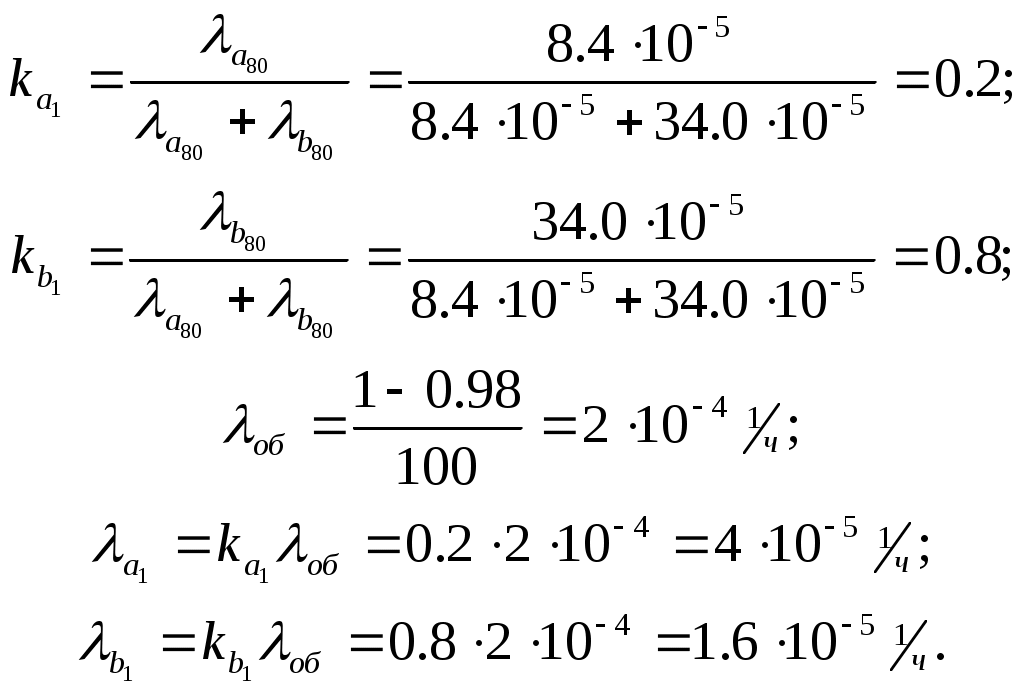 Пример 1-4. Для системы, состоящей из четырех элементов, задано значение параметра потока отказов ωс=10-5 1/ч. Для безотказной работы системы необходима безотказная работа всех элементов, Элементы пронумерованы 1, 2, 3, 4. Распределить заданное значение параметра потока отказов между элементами. Запланированное время проектирования и производства системы равно τ=5 лет, технический ресурс tр=20 лет непрерывной работы. Вложения (затраты) в единицу времени (1 ч) проектирования и производства элементов предполагаются постоянными и для j-го элемента равными: где ωj — параметр потока отказов j-го элемента; Значения kи1=1,6∙10-4 руб.∙отказ/ч2; kп2=kп3=kп4=3∙10-5 руб.∙отказ/ч2; Текущие эксплуатационные затраты в единицу времени также постоянны и равны: Значения kэ1=4∙10-6 руб./отказ; kэ2=kэ3=kэ4=1,7∙10-5 руб./отказ; Общие затраты на проектирование, производство и эксплуатацию системы где Cj — затраты на один j-й элемент; n — число элементов в системе. Решение. Чтобы сравнивать затраты на проектирование, производство и эксплуатацию, их необходимо привести к одному моменту времени — началу эксплуатации элемента. Для этого воспользуемся формулами. Приведенные эксплуатационные затраты в соответствии с (2-6) равны: где Для производственных затрат путем рассуждений, аналогичных приведенным при выводе формулы (2-6), получим: Таким образом, приведенные производственные затраты где обозначено Таким образом, общие затраты на систему Поскольку требуется разделить между элементами заданное для системы значение параметра потока отказов ωс, все ωj при основном (последовательном на логической схеме) соединении элементов связаны соотношением Задача может быть решена при различных видах функции Когда эта зависимость имеет вид, решение упрощается. Можно найти значения всех ωj, при которых общие затраты на систему минимальны. Для этого целесообразно воспользоваться методом неопределенных множителей Лагранжа. Согласно этому методу составляем функцию где γ — неопределенный множитель. Далее приравниваем нулю частные производные этой функции по 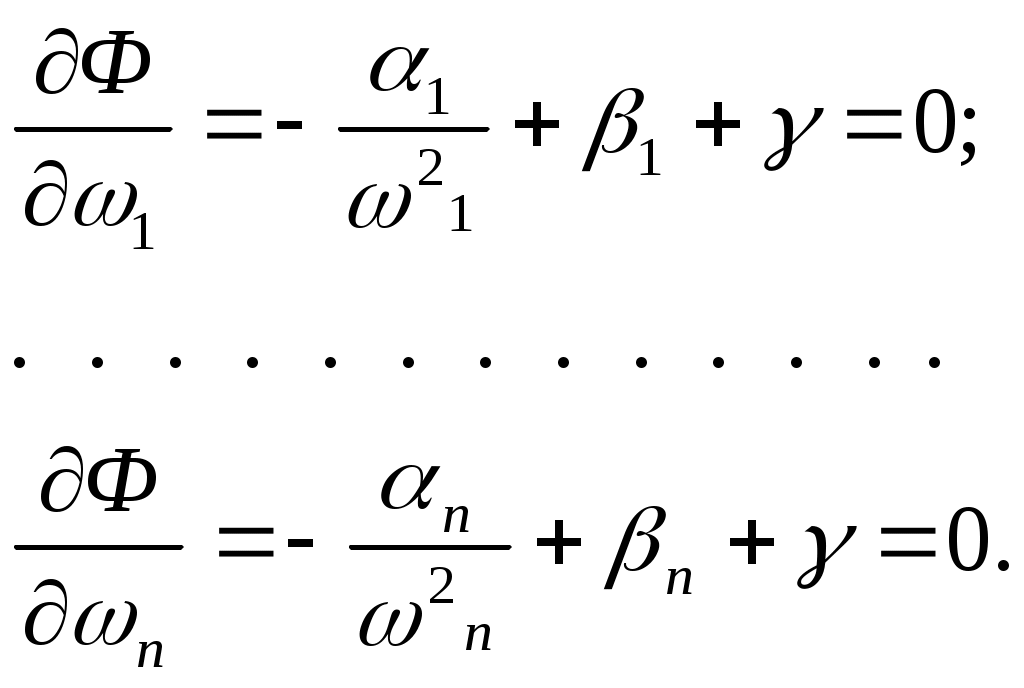 Из этих уравнений получаем: 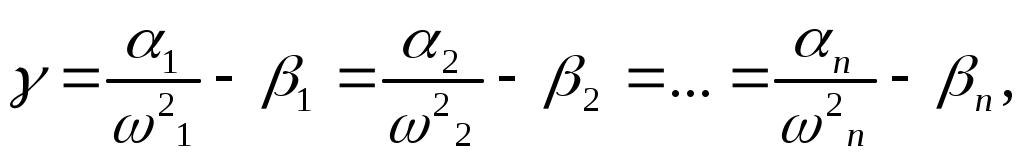 откуда 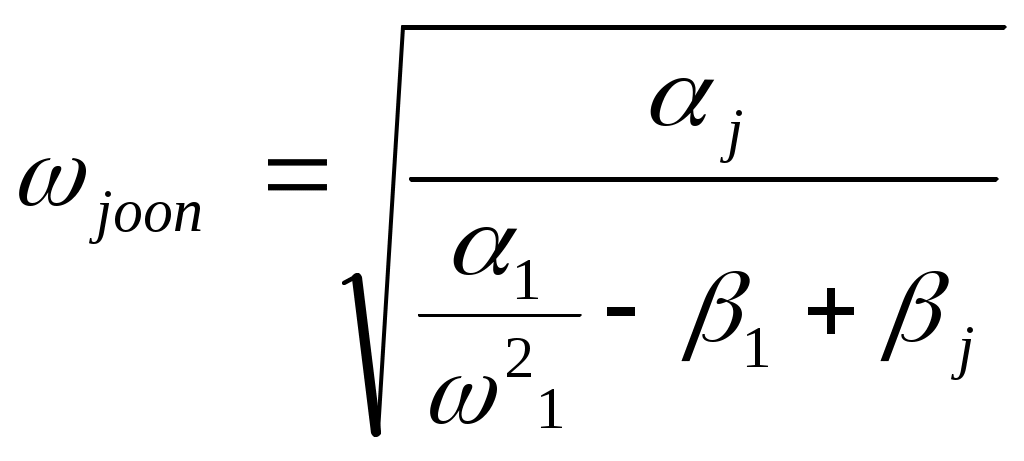 . . 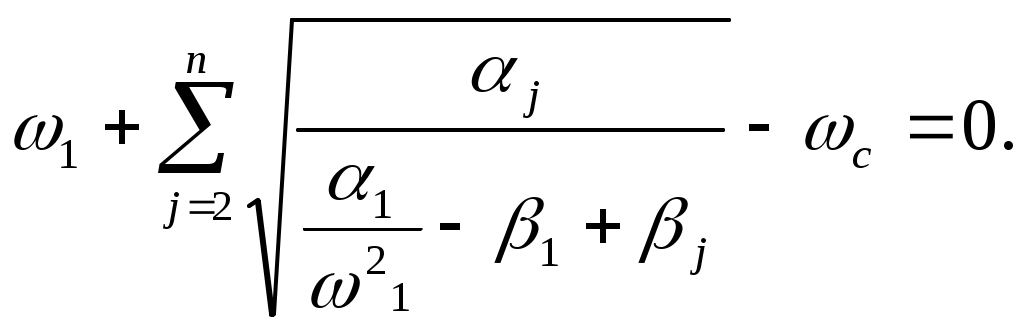 Это уравнение проще всего решить графически, переписав его в виде где 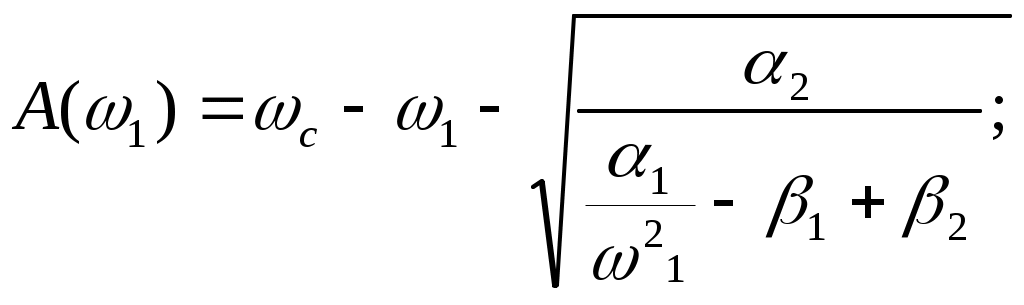 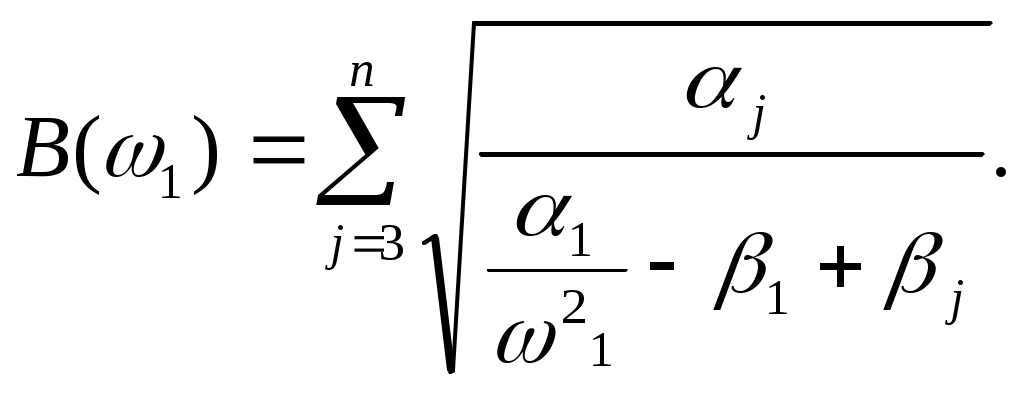 Для графического решения уравнения вычисляются и строятся на графике зависимости A(ω1) и B(ω1). Абсцисса точки пересечения кривых определит искомое значение ω1опт (рис.1.9). 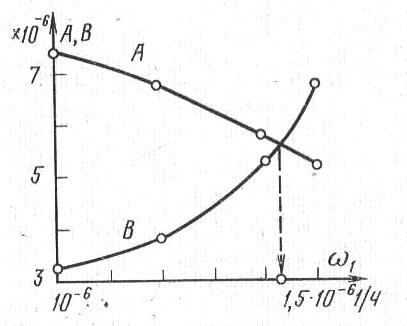 Далее по формуле последовательно определяются все значения ωjопт. Для упрщения вычислений целесообразно переписать формулу в виде 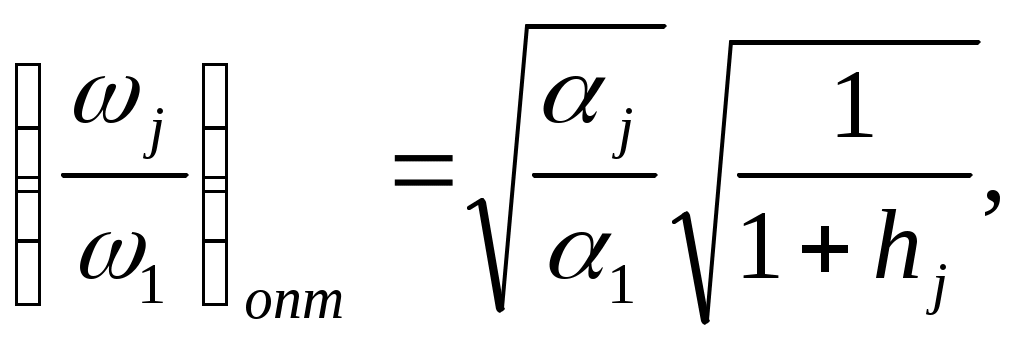 где Рис. 1.9. К вопросу о вычислении ω1опт Для облегчения вычислений по формуле может быть построена номограмма вида рис. 1.10. В правом квадранте осуществляется вычисление Выражения для A(ω1) и B(ω1) можно также записать в виде 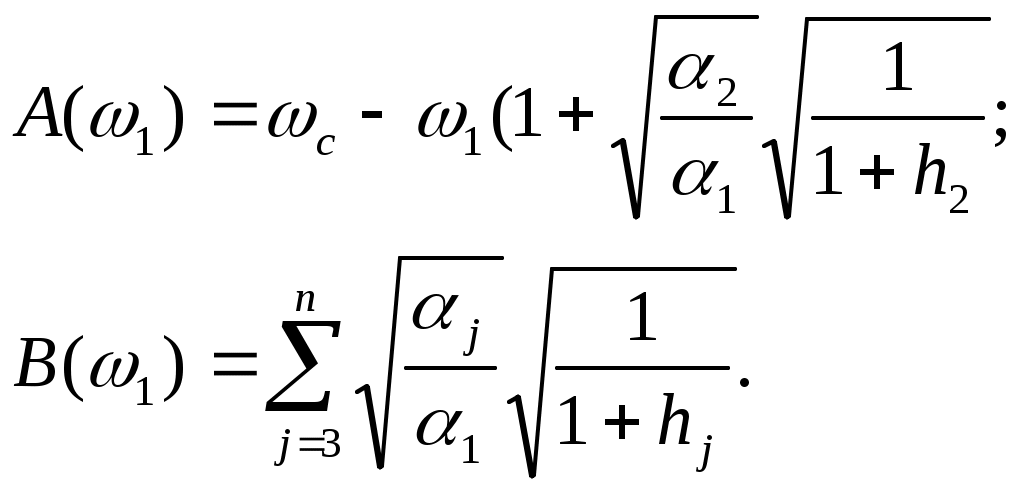 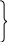 Поочередно задавая значения ω1, можно находить по номограмме значения произведения корней и использовать их согласно формуле. Для рассматриваемого примера 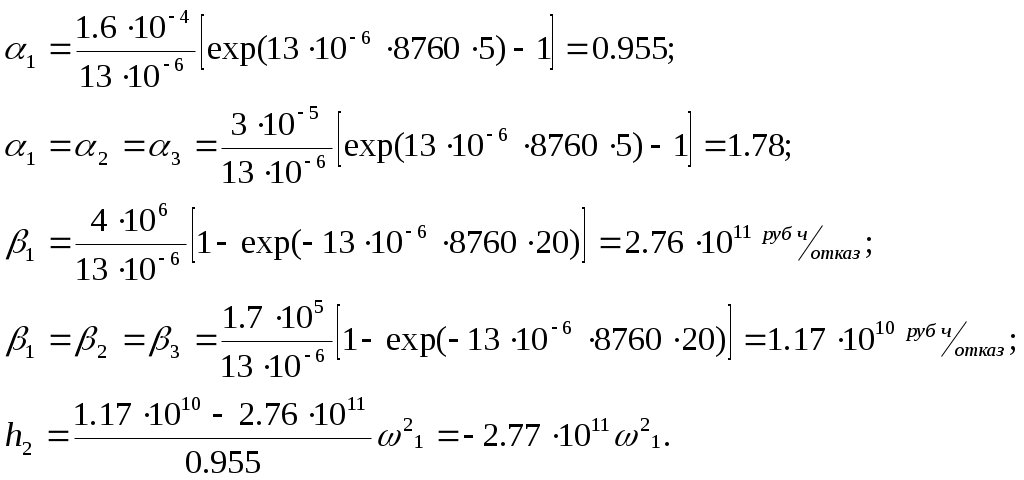 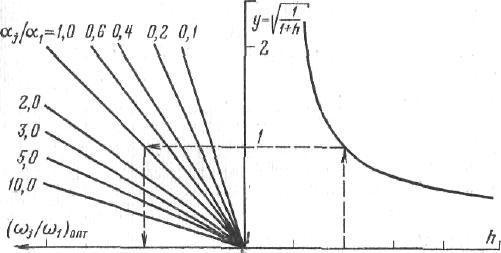 Рис. 1.10 Номограмма для вычисления отношения fi>j/<0]. Используя, строим в одних осях координат графики зависимости A(ω1) и B(ω1) (рис. 1.9). Абсцисса точки пересечения кривых дает ω1опт =1,43-10-6 1/ч. Далее с помощью номограммы на рис. 1.10 определяем: Расчет надежности для последовательно – параллельной структуры: а) при последоватедьном (основном) соединении элементов в устройстве где Р(t)-вероятность безотказной работы устройства;Рi(t) –вероятность безотказной работы i-го элемента. При экспоненциальном законе распределения Р(t)=e-t и последовательном соединении где i-интенсивность отказов i-го элемента устройства. Если Р(t)1, а устрt=0,1 ,то можно воспользоваться упрощенными формулами:  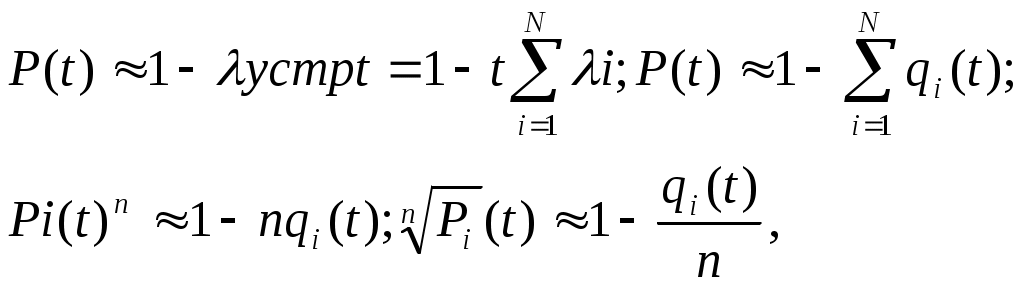 (1.56) (1.56)где qi(t)- вероятность отказа элементов устройства. Пример 1-5*.Система состоит из 1800 элементов, у которых нужно определить Р(50) и Тср, I=0,3*10-6 ч –1: Р(50)=е-1800*0,3*10^-6*50=e-0,027=0,973; 1 1 Т   ср= = 1850 ч. ср= = 1850 ч.устр 5,4*10-4 Примечание:1.Если в условии задачи не упоминается о схеме изделия, принимаем основное, последовательное соединение. 2.Если в условии не указан закон распределения и если =const, принимаем экспоненциальный закон распределения. Пример 1-6. Вероятность безотказной работы блока Рбл(t)=0,95.Блок состоит из 120 равнонадежных элементов. Определить вероятность безотказной работы элемента Рэл(t):  n 1-Рэл(t) 0.05 n 1-Рэл(t) 0.05Р   эл(t)=РЭЛ(t) 1- =1- =1-0.0004=0.9996. эл(t)=РЭЛ(t) 1- =1- =1-0.0004=0.9996.N 120 Пример 1-7. Система состоит из трех устройств:электронного, для которого эл.у.=0,16*10-3ч-1, и двух электромеханических, для которых эл.мех.2=0,06*10-6t2ч-1.Найти Р(100): 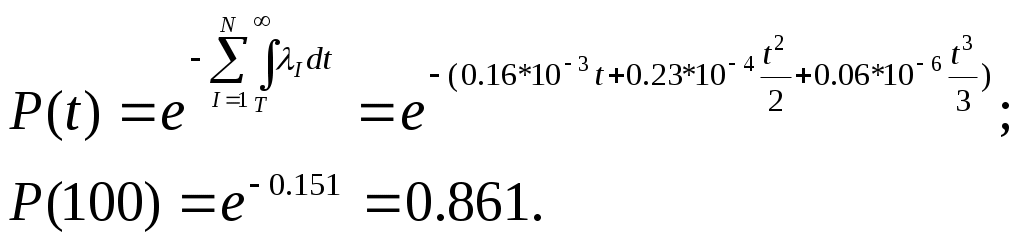 Пример 1-8. Блок состоит из двух модулей.Заданы вероятности безотказной работы модулей Р1(100)=0,95;Р2(100)=0,97; 1 и 2 не изменяются во времени.Найти среднее время безотказной работы блока Тср: Рбл(t)=Р1(t)Р2(t); Рбл(100)=0,95*0,97=0,92; Рбл(100)=е-бл100=0,92; -бл100=ln0,92=-0,083;бл=0,83*10-3ч-1; 1 1 Т   ср= = =1200 ч. ср= = =1200 ч.бл 0,83*10-3 При параллельном соединении элементов в устройстве (резервировании) Пример 1-9. В основной цепочке два элемента n=2;q1(t)=0,05;q2(t)=0,1.Кратность резервирования равнонадежными цепочками равна m=2;t=100ч.Найти вероятность безотказной работы резервированной системы –Р(t) 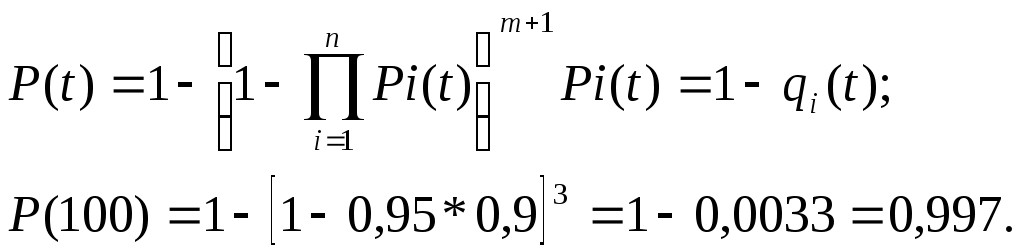 (1.58) (1.58)Пример 1-10. Устройство состоит из двух одинаковых элементов. Конструктор предложил два варианта резервирования с помощью ненагруженных дублирующих устройств (см. рис. 1.2, в, г). Определить, какой из вариантов обеспечивает большую надёжность. Применяем закон гамма-распределения: Зададим значения :эл=0,01ч-1;t=100 ч, тогда Р1(t)/P2(t)=(1+2)/(1+1)2=3/4,т.е. вариант два выгоднее, так как масштаб резервирования мельче. Расчет надежности мостиковой структуры (рис.1.9,б ) Общую вероятность безотказной работы найти невозможно с помощью последовательно-параллельной структуры. Преобразуем треугольник в звезду, как это показано на рис.1.9,в: qa=q1(t)q3(t); qb=q1(t)q5(t); qc=q5(t)q3(t). Далее находим общую Р(t) получившейся последовательно-параллельной схемы (на рис.1.3,г). а 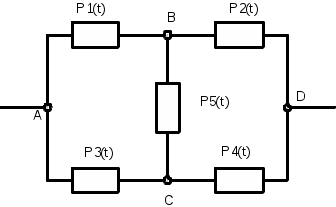 ) б) ) б)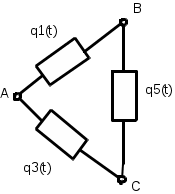 в 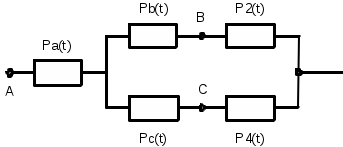 ) г) 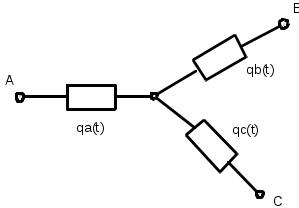 Рис.1.11 Преобразование мостиковой структуры при расчете надежности : а-мостиковая схема ;б,в- преобразование треугольника в звезду;г-эквивалентная схема для расчета мостиковой схемы Пример 1-9-11.Рассчитать надежность мостиковой схемы, если все элементы имеют Рi(t)=0,9;Ра=Рв=Рс=1-(1-Рi(t))2=1-0,01=0,99.Расчет проводим по эквивалентной последовательно-параллельной схеме (см.рис d): Тот же результат можно получить с помощью преобразования по базовому элементу с применением логической схемы расчета надежности . Вероятность отказа n однотипных элементов, вероятность исправной работы n однотипных элементов Вероятность исправной работы группы элементов, подверженных постепенным отказам Расчет надежности элементов, отказавших по причине обрыва (0) или короткого замыкания (КЗ), проводят по формуле В технических устройствах применяются так называемые схемы «четверки», т.е. две параллельные цепочки, с двумя последовательными одинаковыми элементами в каждой цепочке, что соответствует оптимальной надежности при отказах О и КЗ. Кроме рассмотренных методов расчета надежности все шире начинают применять расчет надежности изделий с применением логических схем – универсальный метод расчета надежности. В основу расчета надежности по этому методу положены основные положения алгебры высказываний, раздела математической логики. О сложном событии (отказе изделия) судят по логическим связям между простыми событиями, от которых оно зависит ( отказы элементов). Все логические связи (операции) могут быть сведены к трем: конъюнкции – логическому умножению, дизъюнкции – логическому сложению и отрицанию. Безотказная работа соответствует 1, отказ 0. Конъюнкция графически соответствует последовательному соединению элементов и записывается аb, или а*b и обозначает, что изделие находится в безотказном состоянии, если оба составляющих его элемента находятся в безотказном состоянии. Дизъюнкция графически может быть изображена как параллельное соединение, записывается аb и обозначает, что изделие находится в безотказном состоянии, если в безотказном состоянии находится элемент а, или элемент b, или оба элемента а и b. Отрицаниеозначает, что элементы находятся в отказном состоянии и записываются как Последовательность расчета выполняется по следующим правилам: составляют словесную формулировку условий работоспособности изделия; составляют логическую функцию работоспособности Fл ; осуществляют минимизацию Fл и приведение ее к бесповторной форме по формулам приведения; проводят арифметизацию логической функции Fл FА по формулам арифметизации; проводят расчет надежности изделия; анализируют полученные результаты. Логическая функция работоспособности изделия Fл составляется следующим образом: выделяются наборы (сочетания) простых событий (работоспособностей отдельных элементов изделия), приводящих к работоспособности изделия, и эти события соединяются операцией дизъюнкции. конъюнкции простых событий соединяются операцией конъюнкции. Для расчета надежности восстанавливаемых изделий применяется метод графа переходов. Этот метод пригоден для изделий с простейшим потоком отказов и восстановлений, когда каждый из элементов изделия имеет приблизительно экспоненциальное распределение времени безотказной работы и последующее состояние изделия не зависит от его предыстории. Расчет надежности устройств автоматизации производится при наличии необходимых данных об интенсивностях отказов всех элементов с учетом реальных условий эксплуатации. Точность расчета определяется точностью и достоверностью исходных данных. В инженерной практике расчет надежности производится по среднегрупповым интенсивностям отказов элементов, входящих в автоматическое устройство. Д остаточно широкое распространение получил также коэффициентный метод расчета надежности. в) Коэффициентный способ расчетаПоказатели надежности при этом оцениваются по коэффициентам ki, связывающим интенсивности отказов различных элементов с интенсивностью отказа базового элемента 0 , характеристики надежности которого известны с высокой степенью достоверности: ki=i/0 (1.63) Значения коэффициентов ki , найденные путем анализа данных по интенсивностям отказов различных элементов приведены в таблице 1.3.За основной элемент расчета были приняты резисторы . Чтобы учесть неточность допущения, табл.1.1 приведены максимальные и минимальные значения коэффициентов ki.Таблица 1.3
|
