РАСЧЕТ НАДЕЖНОСТИ АВТОМАТИЧЕСКИХ УСТРОЙСТ6. Расчет надежности автоматических устройств
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
ОЭОЭ ОЭ ОЭ О             ЭО ЭО РЭ РЭ    РЭ РЭ    а) б) ОЭ ОЭ     ОЭ ОЭ           РЭ РЭ    РЭ РЭ    в) г) д) 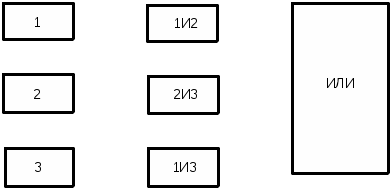                     а-поэлементного;б-общего;в-поэлементного замещением; г- общего замещением;д-мажоритарного;ОЭ-основной элемент; РЭ-резервный элемент СВОЙСТВА РЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ Работающую (включенную) резервированную систему нельзя ремонтировать.Когда в процессе работы системы можно восстанавливать некоторые из отказавших элементов, удается добиться еще большего увеличения надежности. Так как для ремонта элемента необходимо его отключить, восстановление используется при активном методе резервирования. Для нерезервированных систем сокращение времени восстановления ведет к увеличению готовности и практически не влияет на безотказность системы.При наличии резервирования восстановление становится мощным средством повышения надежности.Сокращая время востановления отказавших элементов резервированной системы, можно существенно повысить как готовность, так и безотказность системы.Для восстанавливаемых систем сочетание резервирования с восстановлением имеет столь же большое значение, как для невосстанавливаемых систем сочетание резервирования с профилактическим контролем работоспособности всех элементов (раздельно каждого). Особенности резервированных систем с восстановлением рассмотрим на примере дублированной системы , в которой имеются два одинаковых элемента:основной и резервный.Если переключатель абсолютно надежен, то, уменьшая время ремонта, можно добиться сколько угодно высокой надежности системы. Предположим, что во время ремонта в элементах не могут возникнуть вторичные отказы. Дублированная система может находиться в одном из трех состояний, которые обозначим цифрами:0- система работоспособна (оба элемента работоспособны);1- система работоспособна, но один из элементов отказал (система предрасположена к отказу);2-система неработоспособна (отказала). Обозначим вероятности перечисленных выше состояний через Р0(t), Р1(t), Р2(t).Эти вероятности зависят от начальных состояний системы, в которых она находилась при t=0. В зависимости от назначения дублированной системы к ней могут предъявляться различные требования. После включения система должна безотказно работать заданное время; перерывы в работы не допустимы. При этом необходимо знать вероятность непрерывной безотказной работы системы(вероятность первый раз не оказаться в состоянии 2).Иногда говорят, что для таких систем неработоспособное состояние является поглощающим. При этом вычисляют условные вероятности безотказной работы на интервале (0,t) при условии, что при t=0 основной и резервный элементы работоспособны. Необходимо застать систему работоспособной в заданный момент времени, но перерывы в работе системы не играют роли. При этом рассматриваются готовность системы и ее характеристики: функция готовности Г(t) или коэффициент готовности. Иначе говоря, находится вероятность не оказаться в состоянии 2.Этот случай отличается от предыдущего тем, что имеется возможность перехода из состояния 2 в сосотояние 1. Предположим, что основной и резервный элементы равнонадежны, имеют показательные распределения времени безотказной работы и времени восстановления: 1 =2= , 1 =2=,отказы неработающих элементов невозможны, отказы обнаруживаются мгновенно. Вначале рассмотрим системы, в которых отказы допустимы. На рис. приведены графы состояний четырех возможных вариантов дублированной системы с восстановлением: 2 2 1) 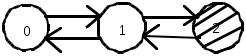  2  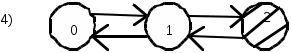 2 Рис.1.3 Графы состояний различных вариантов дублированной системы. нагруженный резерв; при отказах элементов они могут ремонтироваться как по одному, так и одновременно (восстановление без ограничений); нагруженный резерв; отказавшие элементы могут ремонтироваться лишь по одному (ограниченное восстановление); ненагруженный резерв; восстановление производится без ограничений; ненагруженный резерв; восстановление по одному элементу. Дифферециальные уравнения для вероятностей состояний в соответствии с графами состояний рис. имеют вид: для первого варианта 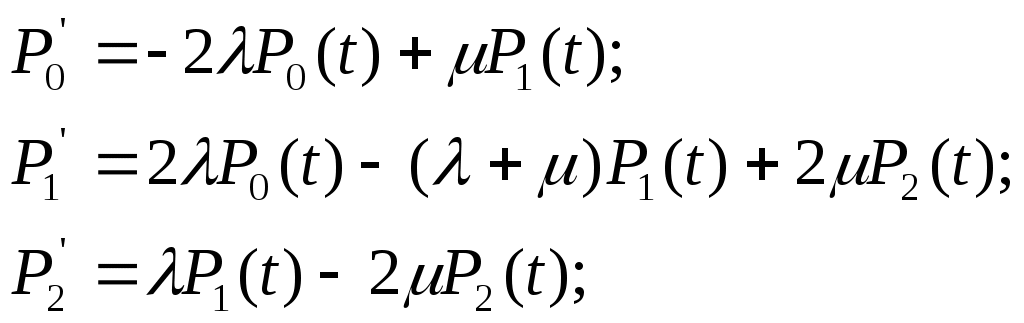 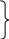 (1.25) (1.25)для второго варианта 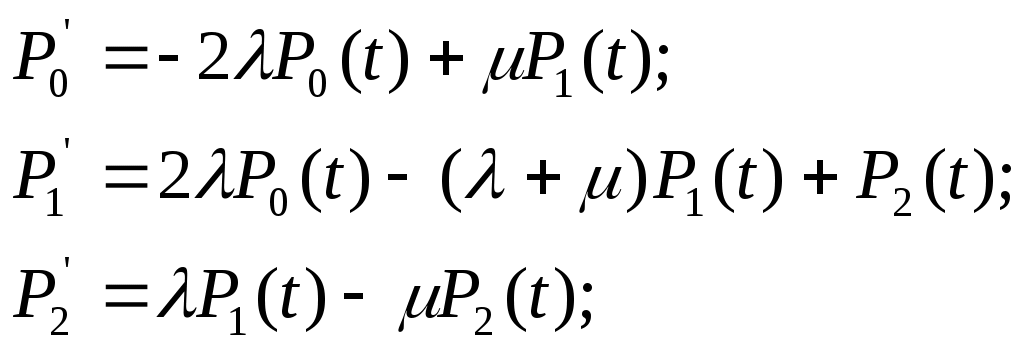 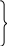 (1.26) (1.26)для третьего варианта 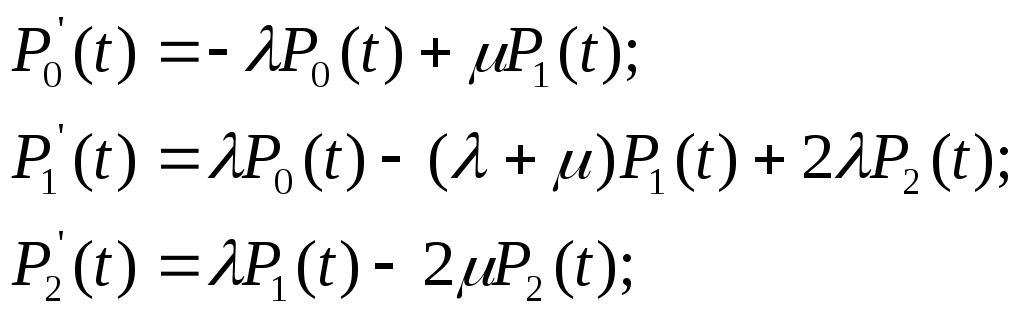 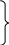 (1.27) (1.27) для четвертого варианта 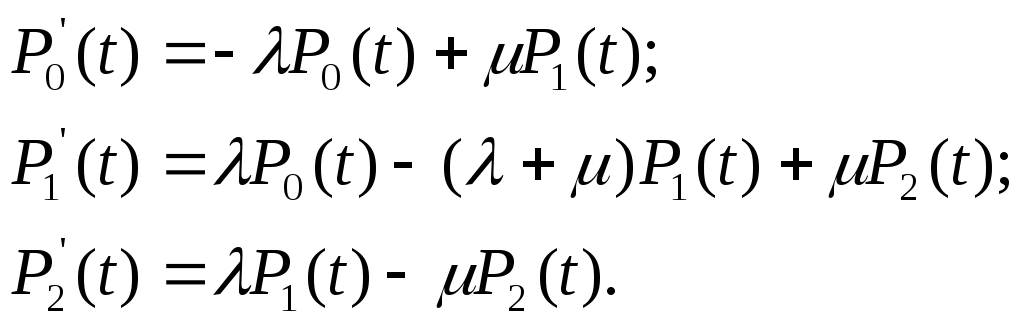 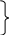 (1.28) (1.28)Эти уравнения должны быть дополнены нормирующим условием В результате решения уравнений при начальных условиях Р0(0)=1; Р1(0)= Р2(0)=0 найдем зависимости Рi(t) для i=0,1,2. Для рассматриваемых систем функция готовности Г(t)= Р0(t)+ Р1(t)=1- Р2(t). (1.30) Функции готовности рассмотренных выше четырех вариантов резервированных систем с восстановлением имеют вид: для первого варианта 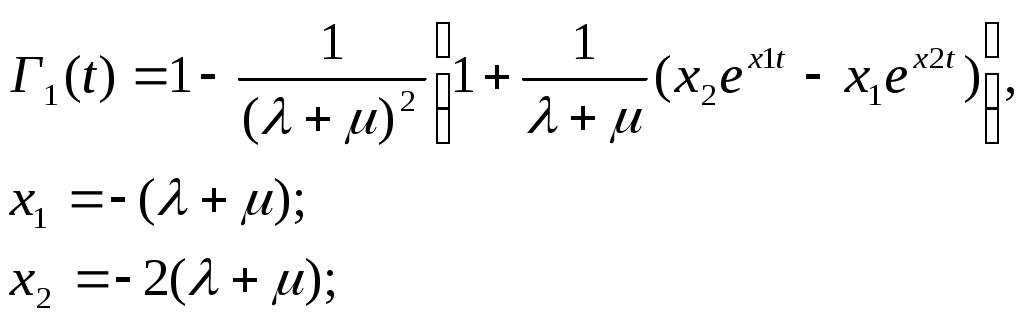 (1.31) (1.31)для второго варианта 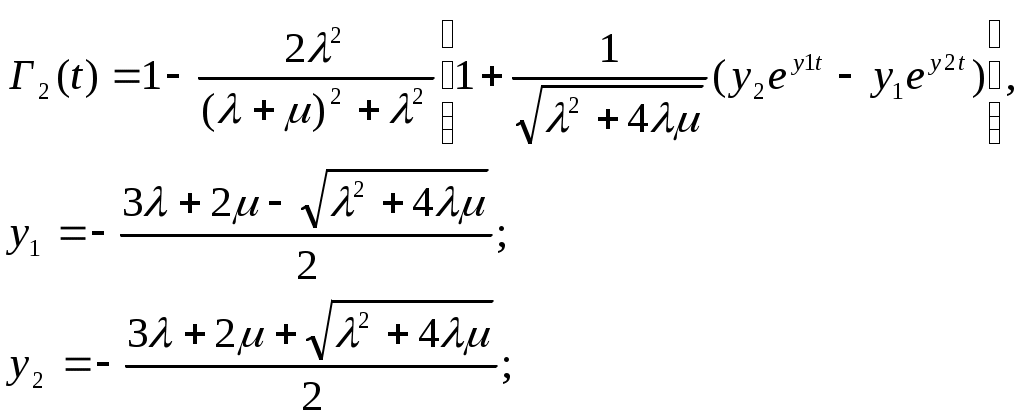 (1.32) (1.32)для третьего варианта 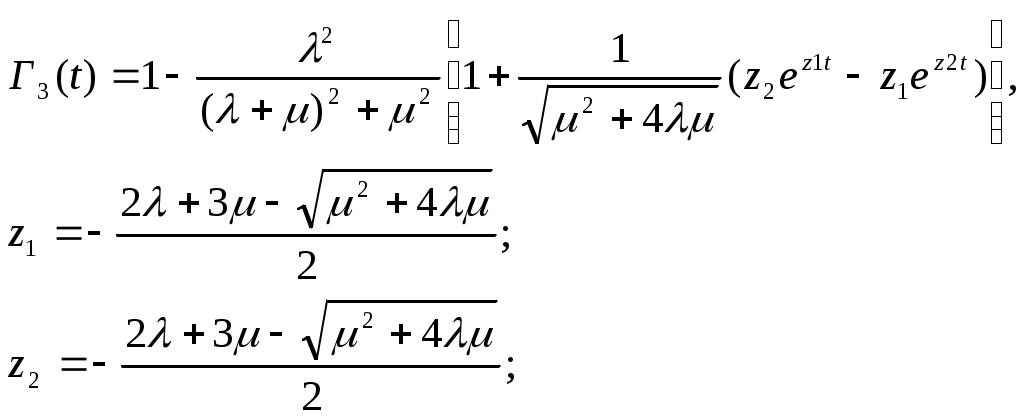 (1.33) (1.33)для четвертого варианта 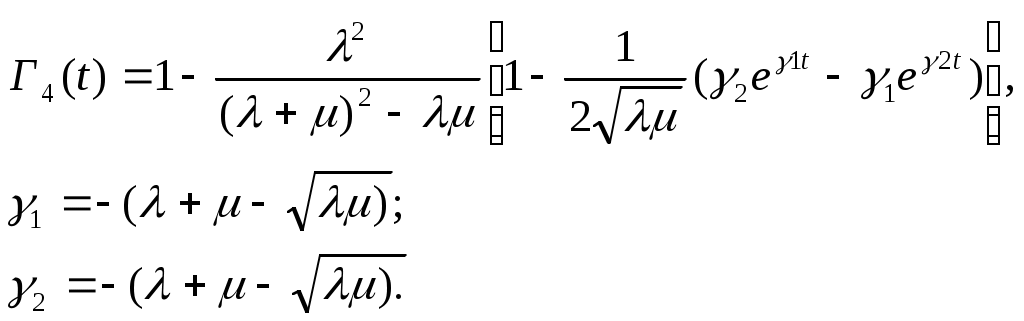 (1.34) (1.34)На рис. Приведены зависимости Г(t) , вычисленные по формулам для =0,01 1/ч и =0,1 1/ч.Для сравнения на графике показана функция готовности Г5(t) нерезервированной системы с теми же значениями и . 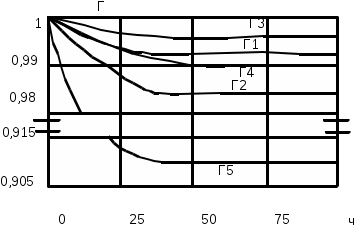 Рис.1.4 Графики функций готовности при =0,01 1/ч; =0,1 1/ч для четырех вариантов дублированной системы, графы состояний которых приведены на рис. Обозначим =/, из формул получим: 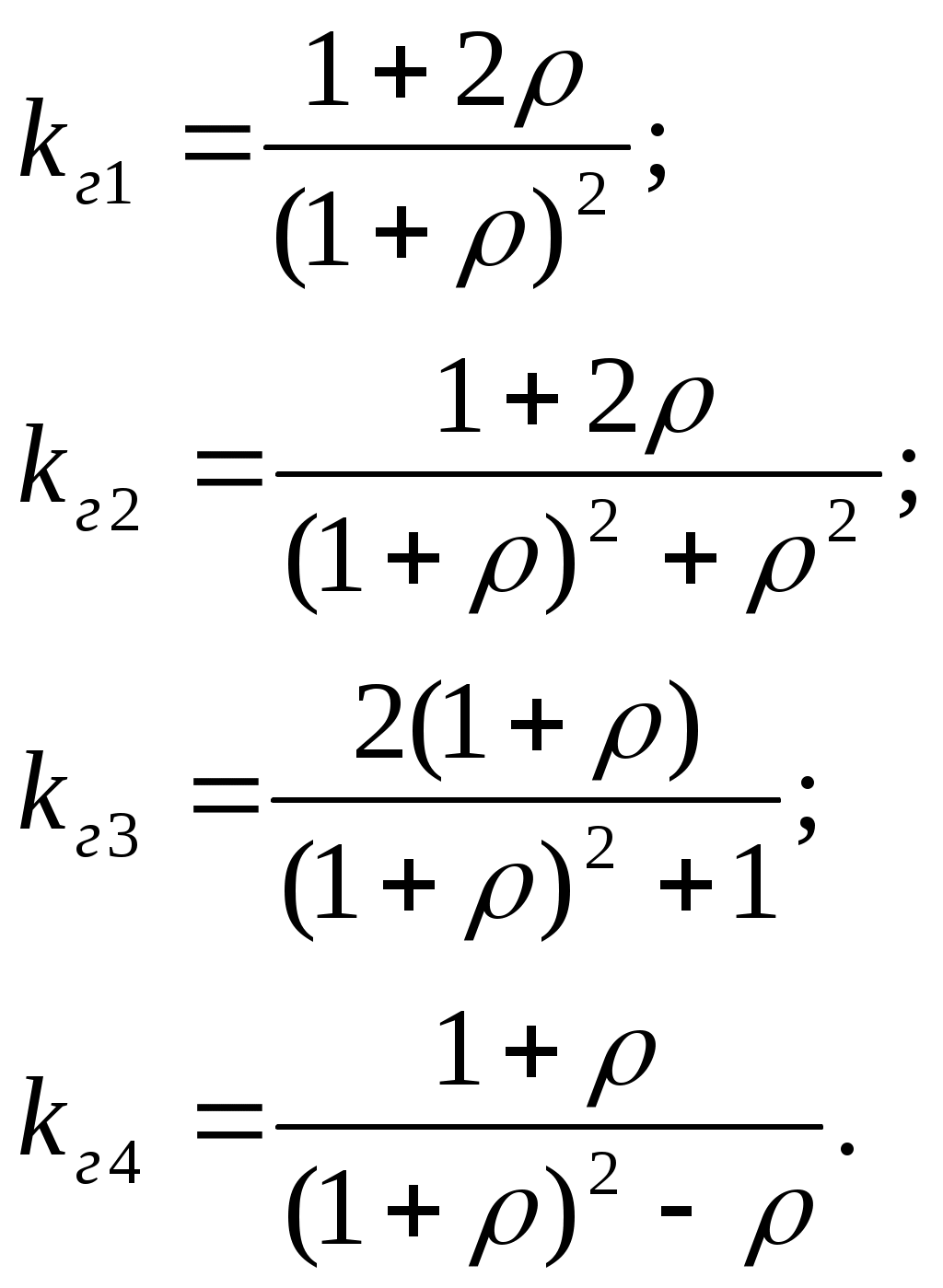 (1.35) (1.35)При =0,1 получаем: kг1=0,992; kг2=0,984; kг3=0,995; kг4=0,991. Таким образом , для повышения готовности восстанавливаемой дублированной системы необходимо стремиться к созданию условий, обеспечивающих осуществления ненагруженного резерва и восстановления без ограничений.Это соответствует и интуитивным представлениям о данном вопросе. Для определения условной вероятности безотказной работы составим системы дифференциальных уравнений при условии, что состояние 2 является поглощающим, т.е. отсутствуют переходы из состояния 2 в состояние 1.При этом в соответствии с графами состояний на рис получим: Для первого и второго вариантов 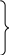 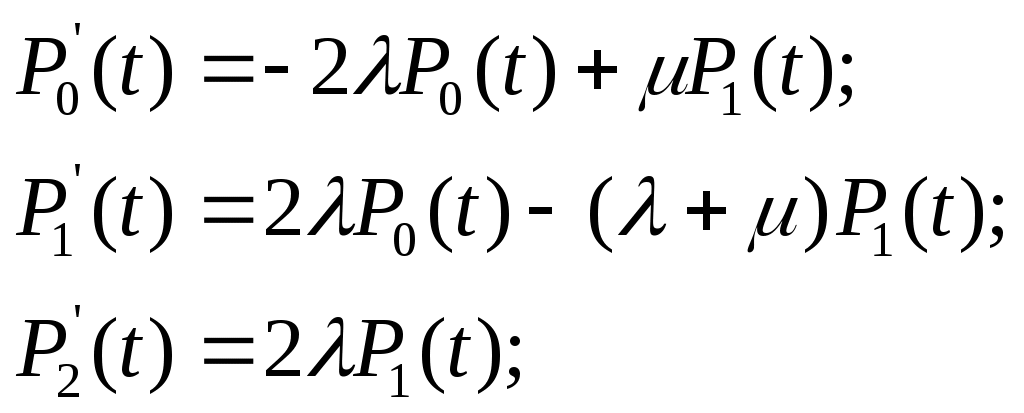 (1.36) Д 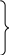 ля третьего и четвертого вариантов ля третьего и четвертого вариантов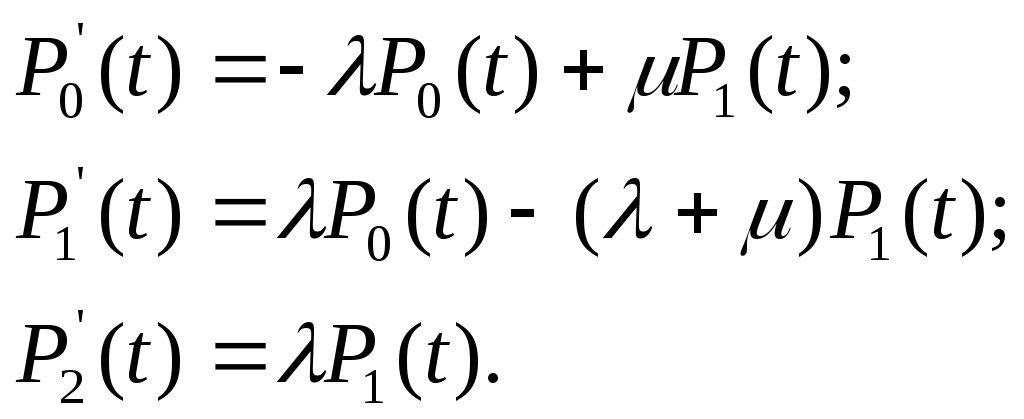 (1.37) (1.37)При начальных условиях Р0(0)=1, Р1(0)= Р2(0)=0 в результате решения систем уравнений и совместно с нормировочным условием получим выражения для условной вероятности безотказной работы: где для первого и второго вариантов для третьего и четвертого вариантов Зависимости р(t), вычисленные по формулам для =0,01 1/ч и =0,1 1/ч, приведены на рис.Здесь же для сравнения приведены графики функций надежности невосстанавливаемых систем: нерезервированной, с нагруженным и ненагруженным дублированием. 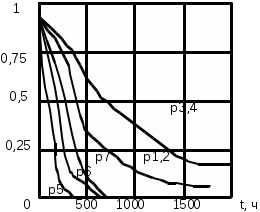 Рис.1.5 Графики функций надежности различных систем при =0,01 1/ч и =0,1 1/ч. Р1,2-для первого и второго вариантов дублированной системы ( графы состояний вариантов приведены на рис.); Р3,4- то же для третьего и четвертого вариантов; Р5- для нерезервированной системы; Р6- для нагруженного дублирования без восстановления; Р7- для ненагруженного дублирования без восстановления. Среднее время безотказной работы резервированной восстанавливаемой системы. Если в начальный момент времени ( при t=0 ) все элементы резервированной системы работоспособны, то среднее время безотказной работы есть время перехода из начального состояния в подмножество неработоспособных состояний. Предположим, что нет ограничений на число ремонтных бригад, отказы обнаруживаются мгновенно, аппаратура контроля безотказна, основной и резервные элементы равнонадежны и имеют показательные распределения времени безотказной работы и времени восстановления. При этом, применяя методы гл. 4(1), можно получить следующие выражения для среднего времени безотказной работы системы с общим резервированием, состоящей из одного основного и k-1 резервных элементов: при ненагруженном резерве в случае /1 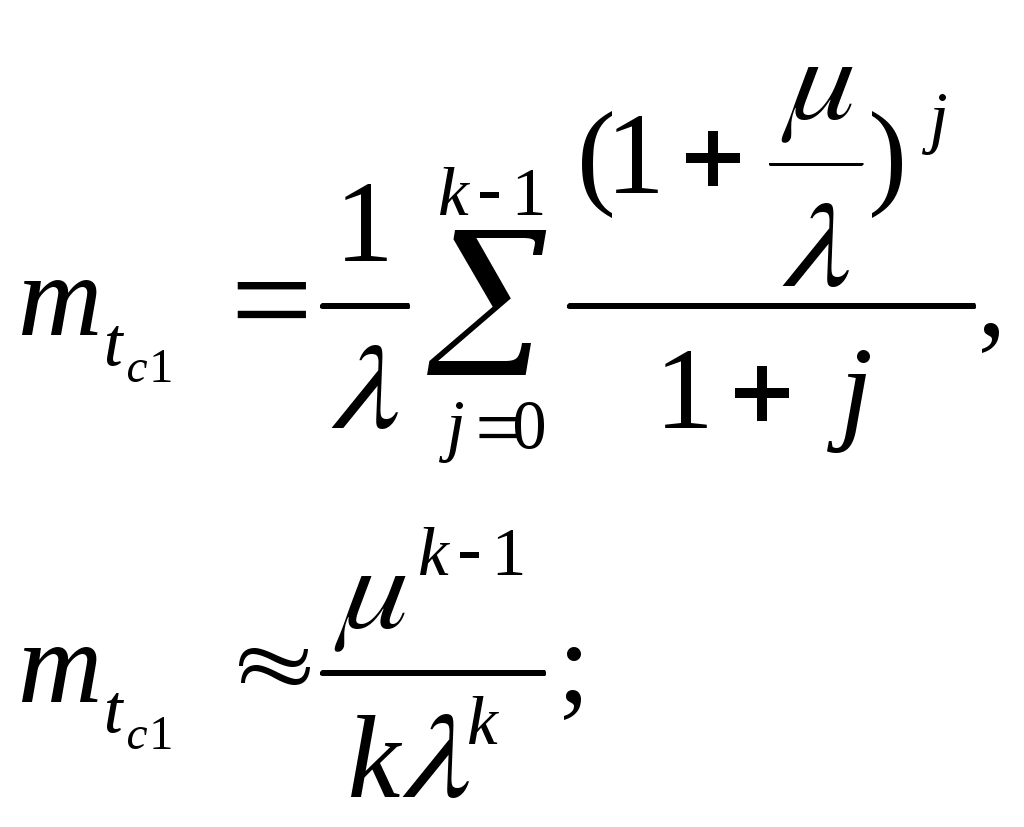 (1.41) (1.41)при ненагруженном резерве 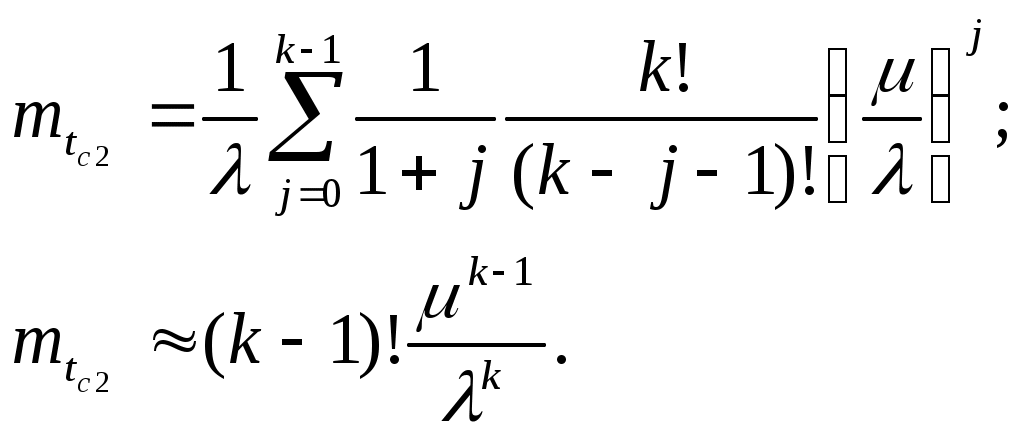 (1.42) (1.42)в случае /1 В реальных системах могут существовать ограничения по числу ремонтных бригад, общему допустимому числу восстановлений и пр.Поэтому значения mtc, вычисленные по формулам, приходится считать верхним пределом среднего времени безотказной работы резервированной восстанавливаемой системы. Значения mtc для практически важных случаев резервирования приведены в табл.1.2 Таблица 1.2
Выражения для mtc при r=1 получены путем составления и решения системы дифференциальных уравнений, соответствующей графу состояний при r=1. Сопоставив выражение для среднего времени безотказной работы дублированной восстанавливаемой системы с нагруженным резервом при идеальном контроле согласно со значением среднего времени безотказной работы невосстанавливаемой системы с нагруженным резервом mtc”=3/2, найдем: mtc/ mtc”=1+/3=1+1/3. Таким образом, при =/=0,01-0,001 применение восстановления повышает среднее время безотказной работы резервированной системы в 30-300 раз. |

