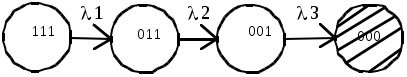РАСЧЕТ НАДЕЖНОСТИ АВТОМАТИЧЕСКИХ УСТРОЙСТ6. Расчет надежности автоматических устройств
 Скачать 1.14 Mb.
|
Расчет систем с неодновременно работающими элементамиВ некоторых системах в различные промежутки времени работает лишь часть элементов (блоков).Такие задачи встречаются при расчете надежности аппаратуры, работающей циклами, когда отдельные блоки выполняют те или иные операции. Для того чтобы система с неодновременно работающими элементами безотказно выполняла свои функции, необходимо, чтобы все ее элементы безотказно работали соответствующее заданное время (наработку).При допущении о независимости первичных отказов элементов вероятность безотказной работы системы, состоящей из n элементов, в течение заданного времени (t0 ,t0+t’) будет:  (1.70)где pj(t0j,t’j)- вероятность безотказной работы j- го элемента в течение времени включения этого элемента t’j= tj - t0j , найденная в предположении, что в момент времени включения t0j этот элемент работоспособен. Таким образом, время ,t’ отсчитывается с момента времени t0 включения системы; время t’j с момента времени t0j включения j- го элемента; t0, t0j, tj отсчитываются с начала эксплуатации системы. Зависимость можно выразить через интенсивности отказов элементов: 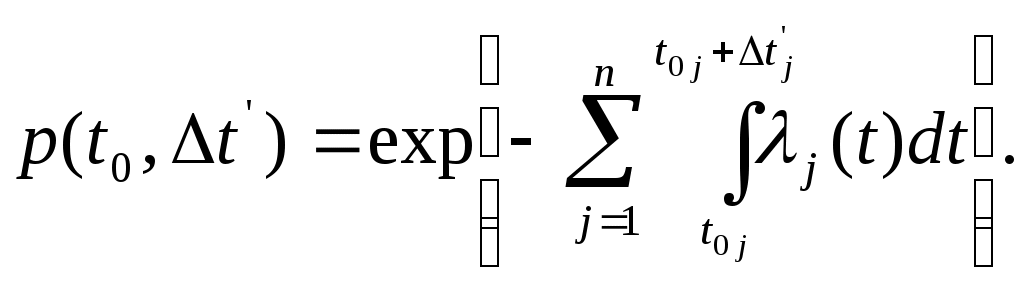 (1.71)Когда интенсивности отказов каждого элемента постоянны, то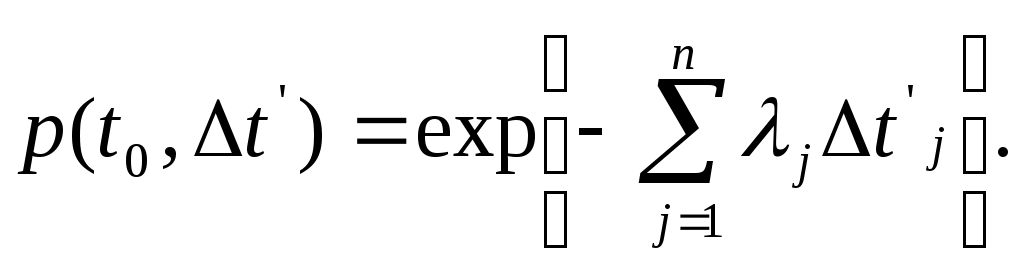 (1.72)При вычислении надежность системы с неодновременно работающими элементами полезно сначала построить график времени работы системы.Пусть система состоит из четырех блоков и имеет график времени работы блоков, изображенный на рис.,а.При этом по формуле будет t01= t02= t0, t03== t0+t’1, t04= t0+t’1+t’3. Вероятность безотказной работы данной системы в течение цикла (t0, t0+t’) будет выражаться уравнением 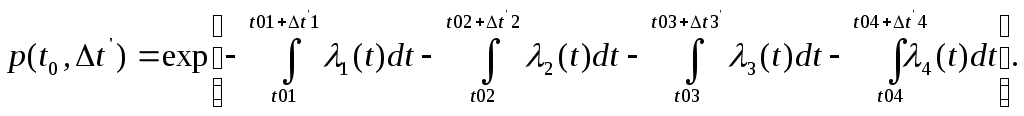 (1.73)Графики времени работы элементов , показанные на рис.1.12 ,а составляются в тех случаях , когда имеется полная уверенность в том, что в момент включения элемент работоспособен. В ряде случаев все элементы системы (как работающие ,так и ожидающие включения) находятся примерно в одинаковых условиях эксплуатации.Если нельзя организовать проверку элементов перед включением с мгновенной заменой неисправных элементов, то график времени работы элементов той же системы в этом случае будет иметь вид , как на рис.1.12,б.Согласно этому графику t01= t02=…= t04= t0. а) 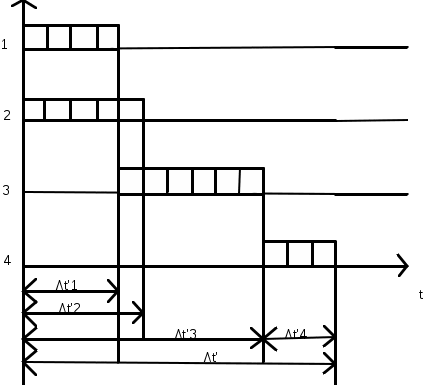 б) 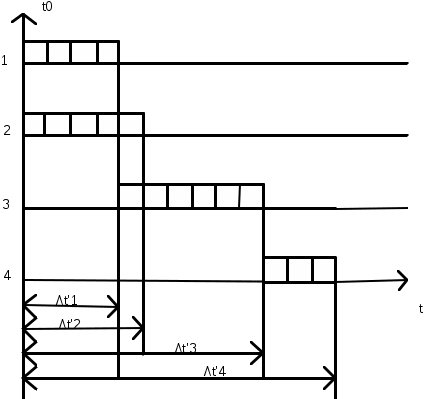 Рис.1.12 Графики времени работы элементов. Учет цикличности работы аппаратуры. Влияние циклического режима работы аппаратуры на ее надежность исследовано неточно. Существует приближенная эмпирическая формула, связывающая общую интенсивность отказов 0, интенсивность отказов при непрерывной работе н , 1/ч, интенсивность отказов на цикл «включено-отключено» ц, 1/цикл , и число циклов включения f за 1 ч непрерывной работы:  (1.74)Отношение Сц=ц/н , ч/цикл, обычно принимается в определенных пределах изменения f постоянным.При этом формула приобретает вид: 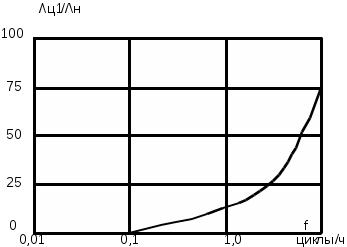  (1.75) Согласно литературы, для американской корабельной электронной аппаратуры Сц=8 ч/цикл при f=0-1,3 цикл/ч.Для авиационной электронной аппаратуры Сц=10 ч/цикл.Сравнительно большие значения Сц для корабельной и авиационной электронной аппаратуры объясняются, по-видимому, увеличенным числом отказов электронных ламп при их частом разогревании и охлаждении в условиях вибрации.В стационарной электронной аппаратуре , где вибрации отсутствуют, значение Сц, по-видимому ,будет небольшим. На рис . приведен экспериментальный график изменения отношения интенсивности отказов при циклическом режиме ц1, 1/ч (при этом ц1=цf), к интенсивности отказов при непрерывной работе н в зависимости от частоты включения f, цикл/ч. Согласно рис. Это отношение при f<0,125 (1 цикл за 8 ч работы) меняется довольно медленно. При f>1 преобладают отказы, вызванные циклическим режимом работы. Работа аппаратуры в непрерывном режиме ведет к уменьшению интенсивности отказов.Однако это может привести к увеличению числа отказов на единицу календарного времени по сравнению со случаем включения аппаратуры только тогда, когда требуется. Например, если аппаратуру, которая должна работать по 4 ч/день, оставить работать в непрерывном режиме круглые сутки, то число отказов за календарное время будет значительно большим , чем в случае включения на 4 ч. Рис 1.13 Зависимость отношения интенсивностей отказов при циклической работе ц1 и непрерывном режиме работы н от частоты f включений по данным. Применение формулы полной вероятности при расчете надежности систем. При использовании формулы полной вероятности учитываются гипотезы Н1,Н2,…Нn – несовместимые события, образующие полную группу.Вместе с одним из этих событий может произойти рассматриваемое событие Х- безотказная работа системы в течение заданной наработки (0,ti). Вероятность появления события Х равна сумме произведений вероятности каждой гипотезы Р(Х/Нj) события при этой гипотезе: 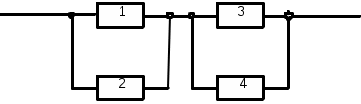 (1.76) При использовании формулы полной вероятности для расчета надежности выбирается определенная группа элементов логической схемы и формируются гипотезы о том , что же произошло с этой группой элементов в течение заданной наработки.Гипотезы могут являться сложными событиями.В каждой из гипотез учитывается , что для любого элемента рассматриваемой группы возможными исходами являются либо безотказная работа, либо отказ. При вычислении условной вероятности безотказной работы системы Р(Х/НJ) при гипотезе НJ предполагается, что произошли соответствующие события (безотказная работа или отказ одного или нескольких элементов) и рассматриваются соответствующие условные логические схемы. Рис.1.14 Логическая схема для расчета надежности системы. В качестве примера применения формулы полной вероятности рассмотрим расчет надежности системы, логическая схема для расчета надежности которой приведена на рис. Рассмотрим группу из первого и третьего элементов. Здесь возможны четыре гипотезы о состояниях элементов: оба элемента остались работоспособными; первый элемент отказал, второй остался работоспособным; первый элемент остался работоспособным, третий отказал; оба элемента отказали. Гипотезы и соответствующие им вероятности приведены в табл. Знаком 1 обозначены работоспособные состояния элементов, знаком 0- неработоспособные.Таблица 1.7
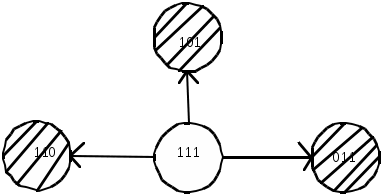
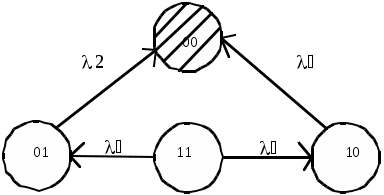
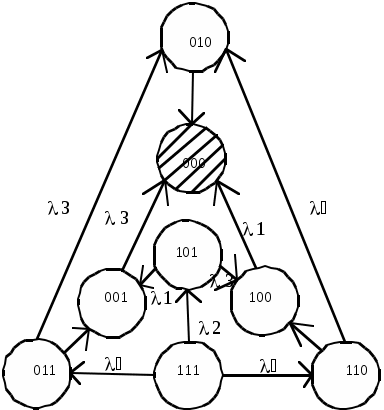
Подставив выражения для Р(Нj) и Р(X/Hj) в , получим после преобразований выражение для вероятности безотказной работы системы:  (1.77) В ряде случаев удобно применять формулу полной вероятности для вычисления вероятности отказа рассматриваемой системы. В любом случае цель применения формулы полной вероятности – сокращение объема математических преобразований и вычислений. Переход от логической схемы для расчета надежности к графу состояний системы. Такой переход необходим при смене метода расчета надежности, при сопоставлении результатов расчетов, выполненных различными методами, для вычисления выигрыша в надежности при переходе от невосстанавливаемой к восстанавливаемой системе и в других случаях.Составление графа состояний восстанавливаемой системы обычно облегчается, если предварительно составить логическую схему для расчета надежности системы, условно ее считая неремонтируемой. Чтобы облегчить переход, целесообразно выделить типовые структуры графа состояний, соответствующие типовым соединениям на логической схеме для расчета надежности. В табл.1.8 Видно, что последовательному логическому соединению соответствует простой ветвящийся граф состояний системы; параллельному ненагруженному соединению- простой неветвящийся граф (последовательная цепочка состояний).Параллельному нагруженному соединению соответствует сложный граф треугольной структуры.Приведенные в табл. Графы состояний при нагруженном дублировании и двукратной избыточности (три параллельно соединенных на логической схеме элемента) охватывают часто встречающиеся на практике случаи. В табл.1.8 Номера состояний обозначены кодом, в котором число знаков равно числу элементов, место знака соответствует номеру элемента, 1 обозначает работоспособное состояние элемента. При равнонадежных элементах соответствующие графы состояний становятся проще. Особенно значительно упрощается граф состояний, соответствующий параллельному нагруженному соединению на логической схеме.Вместе с тем именно при таком логическом соединении на практике часто применяют одинаковые равнонадежные элементы. Графы состояний. Таблица 1.8
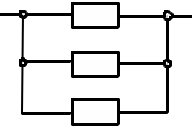
При построении графа состояний целесообразно учитывать типовые структуры табл.1.8 При элементах с различной надежностью система переходит из начального состояния (все элементы работоспособны) к состояниям, каждое из которых соответствует неработоспособности одного из элементов, входящих в последовательные или параллельные нагруженные соединения на логической схеме; при этом остальные элементы работоспособны. При нагруженном дублировании пути графа сходятся к одному состоянию, соответствующему неработоспособности обоих элементов. Состояния, соответствующие неработоспособности элементов ненагруженного резерва, всегда расположены последовательно с состояниями, соответствующими неработоспособности действующих элементов. Учитывая эти особенности структуры графа состояний,целесообразно осуществлять переход от логической схемы для расчета надежности к графу состояний в следующей последоватедьности: В логической схеме для расчета надежности выделяют соединения последовательно-параллельные (нагруженные) и параллельные ненагруженные, объединив элементы в соответствующие подсистемы. Вначале строят граф состояний последовательно-параллельной подсистемы из n1 элементов, начиная с состояния, соответствующего работоспособности всех элементов. Каждое следующее состояние получается из предыдущего путем применения следующих правил: все неработоспособные для данной подсистемы состояний являются конечными; все работоспособные для данной подсистемы состояний являются промежуточными; каждому промежуточному i- му состоянию соответствует n1-i следующих состояний, различающихся неработоспособностью одного из элементов, бывших работоспособными при i-м состоянии системы; новые состояния добавляются до тех пор, пока все состояния не станут конечными; одинаковые состояния(т.е. совпадающие по состояниям элементов) объединяются. По данным правилам строят графы состояний раздельно для нагруженных (работающих) подсистем и подсистем, находящихся в ненагруженном резерве. Конечные состояния графа состояний нагруженной (работающей) подсистемы являются начальными вершинами графа состояний для подсистемы, находящейся в ненагруженном резерве. К каждой из этих вершин необходимо подсоединить граф состояний ненагруженного резерва. На рис.1.15 Приведен пример логической схемы для расчета надежности и соответствующего ей графа состояний. а) 1 2 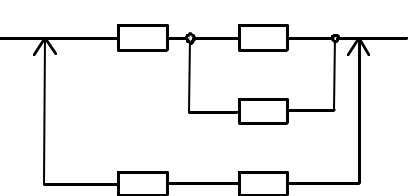 3 4 5 б) 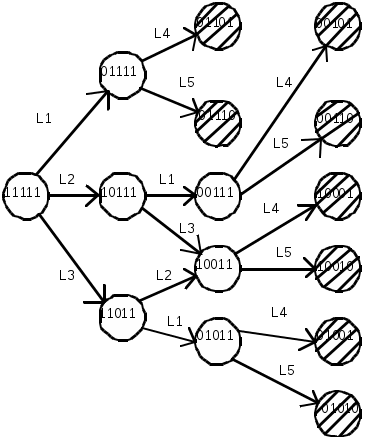 Рис.1.15 Логическая схема для расчета надежности (а) и соответствующий ей граф состояний (б).Заштрихованы неработоспособные состояния. Логико-вероятностный метод расчета надежности систем. Такое условное название получил метод расчета надежности систем, при котором математическая модель системы описывается с помощью функций алгебры логики (ФАЛ), т.е. функций, принимающих лишь два значения (у=1 или у=0) и определяемых различными наборами двоичных аргументов х1 ,х1 , …, хn, которые также могут находиться лишь в двух несовместных состояниях (хj=1 или хj=0). Символы х1, х2,…, хn характеризуют состояния элементов, причем хj=1 соответствует его неработоспособности.Аналогично понимают символы у=1,у=0 для системы. Функцию алгебры логики, связывающую состояния элементов с состоянием системы, называют функцией работоспособности системы.Эту функцию составляют путем анализа физических особенностей работы системы. Обычно имеют дело с монотонными ФАЛ, для которых при любых наборах х=( х1,…, хn) и z=(z1,…,zn), таких, что хj zj, имеет место соотношение у(х)<=у(z). Монотонными являются функции работоспособности систем, в которых замена неработоспособного элемента на работоспособный не может привести к отказу системы. От логической функции работоспособности переходят к уравнению работоспособности в символах обычной алгебры.При этом используют зависимости: если х1 и х2 связаны операцией конъюнкции ,то х1&х2=х1х2; если х1 и х2 связаны операцией дизъюнкции, то х1\/х2=х1+х2-х1х2; если х1 и х2 связаны операцией строго разделительной (исключающей) дизъюнкции («исключающее ИЛИ»), то х1\/ \/х2=х1+х2-2х1х2. При использовании этих зависимостей учитывают, что х1х1=х1. В уравнение работоспособности вместо обозначения простых событий рj и вычисляют вероятность рс нахождения системы в работоспособном состоянии (в течение заданного интервала времени). Например, для системы из трех элементов, логическая схема которой изображена на рис.,б (нагруженное резервирование), функция работоспособности имеет вид: у=х1\/х2\/х3, где номера 1,2,3 – номера элементов.Уравнение работоспособности в символах обычной алгебры у=х1+х2+х3-(х1х2+х1х3+х2х3)+х1х2х3. Выражение для вероятности безотказной работы за заданное время (0,t) рс= р1+ р2+ р3-( р1 р2+ р1 р3+ р2 р3)+ р1 р2 р3, Тот же результат можно получить сразу по логической схеме для расчета надежности: рс=1-(1- р1)(1- р2)(1- р3)= р1+ р2+ р3-( р1 рс2+ р1 р3+ р2 р3)+ р1р2р3. Достоинства логико-вероятностного метода расчета надежности:1) можно применять при любой логической структуре системы (не только при последовательно-параллельных логических схемах;2)можно применять при любых распределениях наработки до отказа. Метод нашел применение для расчета надежности систем, в которых работоспособное состояние связано с наличием электрической проводимости между входом и выходом системы,в частности для энергтических систем. | |||||||||||||||||||||||||||||
