Разработка структурной схемы системы связи
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
Вероятность ошибки в идеальном приемникеВ общем виде вероятность ошибки определяется формулой: 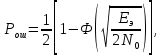 где 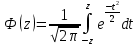 – интеграл вероятностей (табулированная функция); – интеграл вероятностей (табулированная функция); 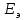 – эквивалентная энергия разности сигналов – эквивалентная энергия разности сигналов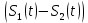 ; ; 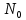 – спектральная плотность помехи. – спектральная плотность помехи.Данная формула является достаточно общей. Для конкретных видов модуляции в канале связи эту формулу видоизменяют, для чего вычисляют соответствующее значение 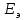 . При этом для различных видов модуляции . При этом для различных видов модуляции 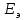 определяется через энергию одного из сигналов, а в окончательную формулу вводят величину определяется через энергию одного из сигналов, а в окончательную формулу вводят величину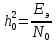 Следовательно, в приемнике Котельникова, который также называется когерентным (в приемнике известна фаза принимаемого сигнала), вероятность ошибки зависит не от отношения мощности сигнала к мощности помехи, а от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличить его энергию за счет увеличения его длительности, что дает дополнительные возможности в построениии помехоустойчивых систем связи. Иначе говоря, в идеальном приемнике Котельникова 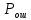 зависит от зависит от 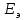 и и 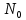 и не зависит от полосы пропускания приемника. и не зависит от полосы пропускания приемника.Сравнительный анализ помехоустойчивости ДАМ, ДЧМ, ДФМПомехоустойчивость приемника определяется вероятностью ошибки при заданном отношении сигнал/помеха. Для разных видов модуляции помехоустойчивость различна. Произведем сравнительный анализ помехоустойчивости ДАМ, ДЧМ, ДФМ. 1. Дискретная амплитудная модуляция (ДАМ). 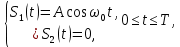 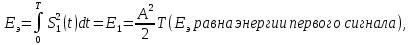 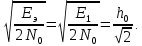 Тогда вероятность ошибки: 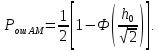 2. Дискретная частотная модуляция (ДЧМ). 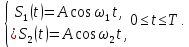 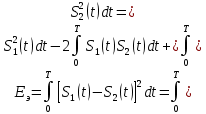 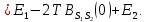 При частотной дискретной модуляции сигналы являются взаимоортогональными, поэтому их функция взаимной корреляции равна нулю. Кроме того, благодаря равной амплитуде сигналов 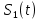 и и 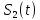 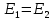 . В результате . В результате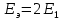 , а , а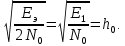 Таким образом вероятность ошибки: 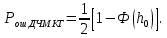 3. Дискретная фазовая модуляция (ДФМ). 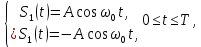 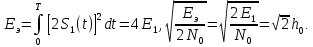 Следовательно, вероятность ошибки: 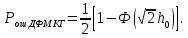 Сравнивая между собой формулы веротности ошибки для различных видов модуляции, видим, что для достижения заданной вероятности ошибки при ДЧМ требуется величина 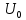 в в 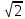 раз больше, чем при ДФМ, а при ДАМ в 2 раза больше, чем при ДФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ – четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции. раз больше, чем при ДФМ, а при ДАМ в 2 раза больше, чем при ДФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ – четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.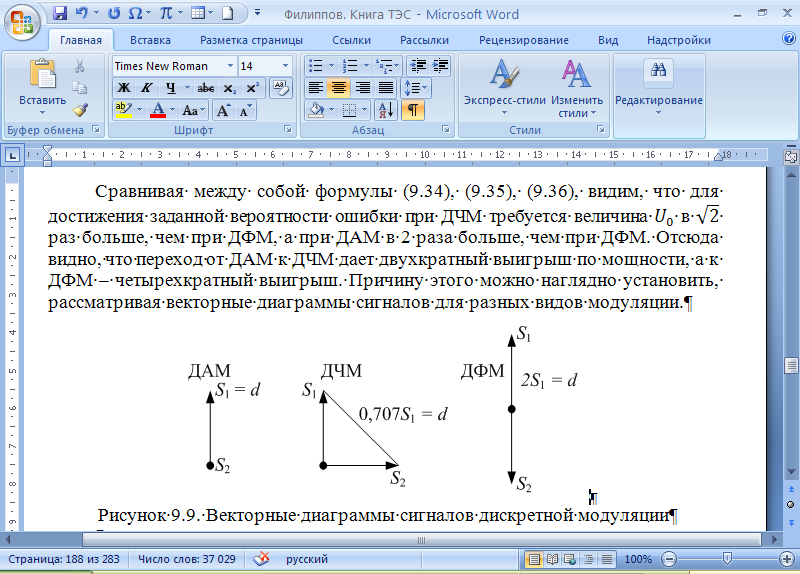 Рисунок 8. Векторные диаграммы сигналов дискретной модуляции Из рисунка видно, что при ДАМ расстояние между векторами сигналов 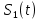 и и 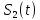 равно длине вектора равно длине вектора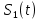 , при ДЧМ (взаимоортогональные сигналы) это расстояние равно , при ДЧМ (взаимоортогональные сигналы) это расстояние равно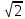 , а при ДФМ (противооложные сигналы) это расстояние равно , а при ДФМ (противооложные сигналы) это расстояние равно 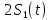 . Энергия же пропорциональна квадрату разности сигналов. . Энергия же пропорциональна квадрату разности сигналов.Следует заметить, что приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ и ДФМ относились к максимальным (пиковым) мощностям этих сигналов. В этом смысле, например, при переходе от ДЧМ к ДАМ мы имеем двукратный выигрыш в пиковой мощности. Однако, сигналы ДАМ имеют пассивную паузу (мощность сигнала в паузе равна нулю), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двухкратный выигрыш. С учетом этого обстоятельства при переходе от ДЧМ к ДАМ двухкратный проигрыш по пиковой мощности компенсируется двухкратным выигрышем за счет пассивной паузы сигналов ДАМ., в результате чего по потребляемой мощности эти сигналы оказываются равноценными. Однако, следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем (решающем) устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная. |
